Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Частотные критерии устойчивости
Критерий Найквиста
Критерий Найквиста, основанный на использовании частотных характеристик, позволяет судить об устойчивости замкнутой САУ по ее амплитудно-фазовой характеристике в разомкнутом состоянии. Установим связь между п.ф. одноконтурной системы в замкнутом и разомкнутом состояниях. Рассмотрим функцию
где числитель представляет характеристический полином системы в замкнутом состоянии, а знаменатель — характеристический полином разомкнутой по цепи главной обратной связи системы. Выражение
есть передаточная функция разомкнутой системы. Так как порядок полинома D(p) для физически реализуемых систем не должен превышать порядок полинома G(p), то характеристическое уравнение замкнутой системы G(p) + D(p) = 0 (6.3) имеет столько же корней, сколько и характеристическое уравнение разомкнутой системы G(p) = 0. (6.4) При выводе критерия Найквиста будем исходить из того, что система устойчива как в замкнутом, так и в разомкнутом состоянии, т.е. вещественные части корней уравнений (6.3) и (6.4) отрицательны. Заменив в уравнении (7.1) р на jω и разложив числитель и знаменатель на простейшие множители, получим уравнение амплитудно-фазовой характеристики замкнутой системы:
где р1, р2,..., рm; s1, s2,..., sm — соответственно корни уравнении (6.3) и (6.4).
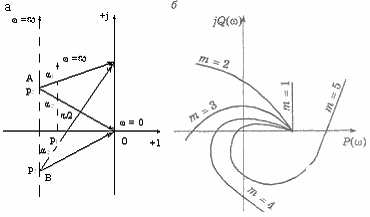
Множители числителя и знаменателя правой части выражения (7.5) представляют векторы, располагаемые в комплексной плоскости слева от мнимой оси (рисунок 6.1, а). Начало каждого вектора лежит в точке, соответствующей корню уравнения рк, а конец — на мнимой оси. При изменении частоты ω от -∞ до +∞ каждый из векторов повернется на угол π. Числитель выражения (6.5) представляет вектор, модуль которого А равен произведению модулей перемножаемых векторов, а аргумент φА — сумме аргументов тех же т векторов. Поэтому при изменении ω от - ∞ до +∞ результирующий вектор D(jω) + G(jω) повернется на угол φА = mπ. Так как по условию корни G(p) = 0 лежат слева от мнимой оси, угол поворота φВ результирующего вектора, имеющего модуль В, при изменении ω от - ∞ до +∞ также будет равен mπ. Нетрудно заключить поэтому, что угол поворота вектора 1 + W(jω) при изменении ω от - ∞ до +∞ равен
φА - φВ = mπ – mπ = 0. (6.6)
Рисунок 6.1 - Пояснения критерия Найквиста: а) расположение векторов р-pi в комплексной плоскости; б) АФХ разомкнутой системы
Амплитудно-фазовая характеристика (АФХ) разомкнутой системы получается путем замены р на jω в уравнении (6.2):
Она отображает границу области устойчивости. При ω→0 W(jω)→an/bm, а при ω→∞ W(jω)→0, если порядок числителя меньше порядка знаменателя (n<m), и W(jω)→а0/b0 при равенстве порядков числителя и знаменателя (n= m). Амплитудно-фазовая характеристика при изменении ω от - ∞ до +∞ симметрична относительно оси абсцисс (рисунок 6.1, б). Если из точки с координатами (-1; j0) провести вектор, который своим концом касается амплитудно-фазовой характеристики, то получим вектор 1 + W(jω), так как О1А = ОА - (-1) = 1 + ОА = 1 + W(jω). При изменении ω от - ∞ до +∞ конец вектора 1 + W(jω) будет скользить по амплитудно-фазовой характеристике, а сам вектор повернется на угол, результирующее значение которого равно нулю. Последнее возможно, если точка (-1;j0) лежит вне амплитудно-фазовой характеристики. Это условие согласуется с условием (2.6), которое возможно лишь в случае, когда система устойчива. Первый критерий Найквиста: замкнутая система будет устойчивой в том случае, если устойчива разомкнутая система и ее амплитудно-фазовая характеристика не охватывает точку (-1; j0). Кривая (рисунок 6.1,б), представляющая частотную характеристику устойчивой системы, пересекается с осью абсцисс справа от точки (-1;jО) и называется амплитудно-фазовой характеристикой первого рода. Кривая (рисунок 7.2,а), пересекающаяся с осью абсцисс и справа, и слева от точки (-1;jО), называется амплитудно-фазовой характеристикой второго рода. В этом случае система в замкнутом состоянии будет устойчивой при условии, если, разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов амплитудно-фазовой характеристики через ось абсцисс слева от точки (-1;jО) равна нулю.
Рисунок 6.2 - Исследование устойчивости по АФХ: а) АФХ второго рода; б) определение запаса устойчивости по модулю и фазе
При анализе устойчивости системы по амплитудно-фазовым характеристикам целесообразно ввести понятие запаса устойчивости по модулю и по фазе. Если через точку (-1;jО) (рисунок 7.2,б) провести окружность единичного радиуса, получим точку пересечения ее с амплитудно-фазовой характеристикой (точка А). Запас устойчивости по модулю характеризуется отрезком h, а запас устойчивости по фазе — углом γ. В общем случае, если степень полинома D(jω) в уравнении (7.7) меньше степени полинома G(jω) и они не имеют общих корней с неотрицательной вещественной частью, критерий Найквиста формулируется следующим образом: САУ, неустойчивая в разомкнутом состоянии, является устойчивой в замкнутом состоянии, если разность между числам положительных и отрицательных переходов АФХ через ось абсцисс слева от точки (-1;j0) равна r/2. Сформулированный ранее критерий устойчивости Найквиста следует рассматривать как частный случай общей задачи при r = 0 (r – число правых корней характеристического уравнения разомкнутой системы).
Критерий Михайлова
Критерий Михайлова дает возможность судить об устойчивости системы по годографу, описываемому концом характеристического вектора замкнутой системы, который может быть получен из уравнения (6.3): М(р) = D(p) + G(p). (6.8) Если заменить р на jω и изменять ω от 0 до ∞, то вектор своим концом опишет в комплексной плоскости кривую, называемую годографом Михайлова. Выражение (6.8) представляет полином m-го порядка, который может быть разложен (при р = jω) на множители по теореме Безу: М(jω) = (jω – p1)(jω – p2)…(jω – рm), (6.9) где р1, р2, …,рm – корни уравнения (6.3). Уравнение (6.9) написано в предположении, что замкнутая система устойчива. Правая часть этого уравнения представляет произведение векторов, расположенных слева от мнимой оси в плоскости корней (рисунок 6.3,а). Так как векторы (jω – pk), соответствующие вещественным корням, совпадают с осью абсцисс, то при изменении ω от 0 до ∞ каждый из них повернется на угол π/2. Каждая же пара комплексно-сопряженных корней повернется при этом на угол π. Действительно, вектор (jω – р2) при изменении ω от 0 до ∞ повернется на угол α1, а вектор (jω – р3) на угол α2. Так как ∟ABO = ∟BAO = α2 (ΔOAB — равнобедренный), то результирующий угол поворота обоих векторов α1 + α2 = π. Таким образом, вектор М(jω), представляющий произведение m векторов, аргументы которых при умножении складываются, повернется при этих условиях на угол m(π/2). При ω=0 годограф Михайлова отсекает на вещественной оси в положительном направлении отрезок, равный свободному члену характеристического уравнения. Начало характеристического вектора совпадает с началом координат. Поэтому, если система устойчива, характеристический вектор при своем вращении нигде не должен обращаться в нуль. Критерий Михайлова формулируется следующим образом: замкнутая система устойчива в том случае, если вектор кривой Михайлова при изменении ω от 0 до ∞ проходит в положительном направлении m квадрантов комплексной плоскости, начиная свое движение от положительной вещественной полуоси, и при этом нигде не обращается в нуль (m – порядок характеристического уравнения замкнутой системы).
Рисунок.6.3 – Исследование устойчивости по Михайлову: а) график к доказательству критерия Михайлова; б) годограф Михайлова
На рисунке 6.3,б приведены годографы Михайлова для устойчивых замкнутых систем, описываемых уравнениями различных порядков (m = 1, 2, 4, 5). Система будет неустойчивой в случае, если полином M(jω), определяемый уравнением (7.9), имеет корни с положительной вещественной частью. Число этих корней r можно определить по виду годографа. Если полный угол поворота вектора M(ω) равен (m – 2r)(π/2), то число правых корней равно r. Значение частот ωi, при которых кривая Михайлова пересекает вещественные и мнимые полуоси комплексной плоскости, находят из уравнений: Х(ω) = 0 (6.10) У(ω) = 0 (6.11) Вещественную Х(ω) и мнимую У(ω) части функции Михайлова М(ω) можно представить графически (рисунок 6.4).
Рисунок 6.4 – АФХ замкнутой САУ: а) устойчивая; б) неустойчивая
В соответствии с критерием Михайлова для устойчивой САУ будет обязательно выполняться условия (рисунок 6.4,а): ω0 < ω1 < ω2 < ω3 <.....< ωn (6.12) Если корни ωi уравнений (6.10, 6.11) будут немонотонно возрастать, то САУ будет нестойчивой (рисунок 6.2,б). Следствие критерия Михайлова: система будет устойчива, когда вещественная и мнимая части функции Михайлова приравненные к нулю, имеют все действительные и монотонно возрастающие корни, при чем общее число этих корней равно порядку характеристического уравнения n, и при ω = 0 Х(0)>0 и У(0) = 0. Для уравнений до шестого порядка включительно можно легко определить устойчивость, не вычерчивая кривую Михайлова, а определяя только чередование знаков Х(ω) при подстановке корней с возрастанием ωi, найденных из уравнения (6.11) У(ω) = 0.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.70.255 (0.019 с.) |
 (6.1)
(6.1) (6.2)
(6.2) (6.5)
(6.5)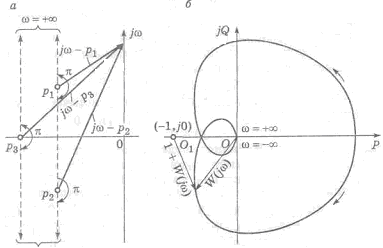
 (6.7)
(6.7)