
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В уравнениях на основе размерностей
Метод установления характера зависимостей между физическими величинами на основе сопоставления их размерностей называется методом анализа размерностей. Методики применения анализа размерностей для выявления закономерностей функциональных связей физических величин достаточно разнообразны. Здесь рассмотрены некоторые достаточно известные в специальной литературе примеры решения практических задач с помощью анализа размерностей. Задача 1.13. Висящий на пружине груз массой m уравновешивается силой ее натяжения (рис.1.1). Приложение силы F к грузу вызывает изменение его положения относительно исходного за счет растяжения пружины. В новом равновесном положении удлинение пружины составляет a. Устранение силы F вызывает возвращение груза в исходное положение за счет сокращения пружины. Требуется определить время сокращения пружины t в зависимости от массы груза m, удлинения пружины a и жесткости пружины k. В данном случае время рассматривается как функция известных физических величин a, m и k. В состав этой функции могут входить не только члены степенного характера (как в большинстве определяющих уравнений), но и какие-либо тригонометрические, показательные или другие неалгебраические функции. Аргументом таких функций могут быть только безразмерные величины. Это вытекает из положения теории размерностей, устанавливающей, что единицы величин, входящих в аргументы неалгебраических функций, не должны изменяться при любом изменении единиц, принятых за основные. Эти единицы величин должны образовывать безразмерную комбинацию. В системе единиц физических величин LMT из величин a, m и k, размерностями которых равны соответственно L, M и MT– 2, безразмерной комбинации величин составить невозможно. Это видно из того, что T входит только в размерность k, а в безразмерную комбинацию входить не может. Величины a и m по определению не могут дать безразмерной комбинации. Следовательно, единственно возможным видом связи между a, m и k является алгебраическая функция. Представляется естественным искать данную функцию в виде произведения степенных членов, т.е. в виде рассмотренных ранее определяющих уравнений: t = C aPmq ky, где C – неизвестный безразмерный коэффициент пропорциональности; p, q, y – неизвестные показатели степени. Приравнивая размерности левой и правой частей данного уравнения, получим
T = Lp · Mq Полученное уравнение будет инвариантным (неизменным) по отношению к размеру основных единиц измерения. Исходя из этого условия, получаем следующие уравнения для показателей степеней: P = 0; q+ y = 0; – 2 y = 1, откуда y = – 1 / 2и t = C Точное решение задачи, основанное на применении законов механики, приводит к тому же уравнению, но с коэффициентом C = π/2. Задача 1.14. Из цилиндрического сосуда площадью сечения S 1 вытекает идеальная (не имеющая вязкости) жидкость плотностью ρ через отверстие площадью сечения S 2 в дне сосуда. Жидкость в сосуде налита до уровня h от дна (рис.1.2). Определить время вытекания жидкости t. Логика обоснованного применения произведения степенных членов для размерности времени такова: вытекание жидкости происходит под действием силы тяжести. Можно предположить, что в числе величин, обусловливающих процесс вытекания, присутствует ускорение свободного падения g. В функции связи всех известных величин возможно присутствие трансцендентной функции, включающей в свой аргумент величины h, S 1и S 2, (величины ρи g в этот аргумент входить не могут, так как они могут тогда изменяться при изменении основных величин). Определяемое время можно представить в виде произведения степенных членов: t = C ρ p gq hr S Уравнение размерности имеет вид T = L– 3 p Mp · Lq Т – 2 q · Lr · L 2 k · L 2 l . (1.19) Приравнивая показатели степени правой и левой частей, получим систему уравнений: 0 = – 3 p + q + r + 2(k + l), 0 = p, 1 = – 2 q. Для определения пяти показателей имеются только три уравнения, но два показателя определяются непосредственно: p = 0, q = – 1/2. Это означает, что время вытекания жидкости не зависит от ее плотности и обратно пропорционально корню квадратному из ускорения свободного падения. Для определения оставшихся показателей степени следует ввести дополнительные данные или сделать уточняющее предположение о ходе процесса вытекания жидкости. Предположим, что скорость жидкости в отверстии не зависит от его сечения. В этом случае время вытекания должно быть обратно пропорционально S 2. Вместе с тем время вытекания при одинаковом начальном уровне жидкости h должно быть пропорционально общей массе жидкости и, следовательно, S 1. Тогда значения показателей k и l будут равны соответственно 1 и –1. При таком предположении сразу же определяется показатель r = 1/2 и для времени вытекания получается выражение
t = C Коэффициент С, как и в задаче 1.13, не может быть определен анализом размерностей. Расчет в гидравлике показывает его значение, равное Определение показателя степени r можно осуществить, если единицу площади отнести к основным, не связывая ее с длиной. Такой прием возможен, так как о форме отверстия S 2. и форме сечения сосуда S 1 ничего не говорится. Тогда уравнение размерности для времени вытекания будет иметь вид T = L – 3 p Mp · Lq T – 2 q · Lr ·Σ 2 k ·Σ2 l, где Σ – условное обозначение размерности площади. Из этого уравнения дополнительно к условиям p = 0 и q = –1/2 получается k = –1, r = 1/2. Окончательно решение задачи имеет вид T = C Здесь в отличие от предыдущего решения неизвестной является функция отношения площадей φ Благодаря введению одной общей единицы, в решении задачи достигнута большая определенность. Пример 1.15. Определить скорость v, которую приобретет тело массой m под действием силы F в конце пути h. Как и в предыдущем примере, представим скорость в виде произведения соответствующих степенных членов с неизвестным коэффициентом пропорциональности: V = C · Fp · mq · hr. (1.20) Уравнение размерностей будет иметь вид LT– 1 = LpMpT –2 p · Mq · Lr. (1.21) Сопоставляя показатели степени, получим уравнения: r + p = 1; p + q = 0; –2 p = –1. Отсюда получаем p = 1/2; q = –1/2; r = 1/2. Тогда уравнение для v имеет вид v = C Решение данной задачи можно найти не на основе определения силы по второму закону Ньютона, а по закону всемирного тяготения. При этом гравитационную постоянную уподобим безразмерному коэффициенту пропорциональности, равному постоянному числу, например единице. В этом случае размерность силы станет равной dim F = L– 2 M 2. Уравнение размерностей, представленное в виде произведения степенных членов, будет иметь вид LT –1 = L– 2 p M 2 p · Mq Lr. Анализируя данное уравнение, можно увидеть, что здесь имеет место ошибка. В левой части размерность времени имеет степень –1, а в правой части время отсутствует. Причина такого несоответствия заключается в том, что из рассмотрения процесса движения тела выпало ускорение под действием силы. В рассматриваемой системе единиц измерения, в которой единица силы определяется по закону всемирного тяготения, в выражении для второго закона Ньютона должна стоять инерционная постоянная, размерность которой равна dim k = L– 3 MT 2 (раздел 1.7, уравнение 1.17). Введя в уравнение размерностей (1.21) размерность инерционной постоянной, получим с учетом выражения (1.20) три совместных уравнения, которых недостаточно для определения четырех степеней, т.е. LT– 1 = L– 2 p M 2 p · M q Lr · L– 3 k M k T 2 k . Отсюда получаем систему уравнений: 1 = – 2 p + r – k,0 = 2 p + q + k, – 1 = 2 k, из которой определяется только k = –1/2. Можно один показатель степени оставить неизвестным в анализируемой зависимости, которая представится в виде
V = CF p Решение может быть доведено до конца, если ввести в качестве основной меры величины единицу силы F с одноименной размерностью dim F. Размерность инерционной постоянной будет равна на основании уравнения F = kma: dim k = L– 1 M– 1 T 2 F. Уравнение размерностей для рассматриваемой выше зависимости запишется на основании уравнения (1.21) в следующем виде: LT– 1 = Fp · Mq · Lr · L–k M–k T 2 k Fk. Находим для показателей степени систему уравнений: 1 = r – k; 0 = q – k; – 1 = 2 k;0 = p + k. Отсюда определяются все показатели степени: p = r = 1/2; q = k = – 1/2. Уравнение скорости имеет вид v = C Из рассмотренного видно, что, если уменьшить число основных единиц, приняв для решения задачи систему с двумя основными единицами длины и времени (единица массы будет производной), в которой размерности силы и массы равны соответственно dim F = L 4 T– 4, dim m = L 3 T –2, решение задачи становится неопределенным. Действительно, написав уравнение размерностей в виде LT– 1 = L 4 p T– 4 p · L 3 q · T –2 q · Lr, можно получить только два уравнения для нахождения показателей степеней: 1 = 4 p + 3 q + r; – 1 = – 4 p – 2 q. Решение задачи становится неопределенным и требует дополнительных предположений или изменения условий. Уравнения разрешимы, если подставить значения показателей степеней, найденных для уравнения (1.19). П-теорема Существенную помощь при анализе размерностей оказывает так называемая П-теорема, сущность которой рассматривается ниже. Физические закономерности явлений представляют собой функциональные зависимости между величинами, которые характеризуют данные физические явления. Численные значения этих величин находятся в зависимости от принятых систем единиц измерений, но закономерности явлений от выбора системы не зависят. Допустим, размерная величина a является функцией независимых между собой размерных параметров a 1, a 2, …, an: Среди этих параметров могут быть как переменные, так и постоянные величины. Можно принять первые k величин из a 1, a 2, …, an в качестве основных, т. е. с независимыми размерностями (k £ n). Для того чтобы решение задачи было определенным, число основных единиц должно быть больше или равно k. Независимость означает, что формула размерностей для одной из основных величин не может быть выражена в виде произведения степенных членов, представляющих размерности других величин. Например, если в уравнение (1.22) входят значения длины, времени, скорости и плотности вещества, то независимыми в системе СИ будут размерности длины, времени и плотности вещества (L, T и L– 3 M), а зависимой – размерность скорости (LT– 1). Независимость размерностей первых k величин позволяет отнести их фактически к числу основных величин:
dim a 1 = A 1, dim a 2 = A 2 , …,dim ak = Ak . Соответственно размерности для оставшихся величин a k+ 1, a k+ 2 , …, an примут вид: dim ak+ 1 = dim a n = Так как a 1, a 2 ,..., ak представляют собой числовые значения величин с независимыми размерностями (фактически основные единицы), единицы измерения каждой из них можно изменять в произвольное число раз. Числовые значения остальных величин (от a k+ 1до a n) также изменятся в соответствии с их размерностями, если изменить единицы измерения первых k величин таким образом, чтобы числовые значения каждой из них стали равными числу 1. Для этого следует умножить каждое из значений a 1, a 2 , …, ak на 1/ a 1, 1/ a 2 ,..., 1/ ak. Значения величин согласно размерности станут равными: для размерной величины a в общем виде
для остальных n – k величин Здесь П – комплексы отношений величин. Обозначение П (или π) принято по первоначально используемым символам при создании основ теории подобия. Уравнение (1.23) примет вид П = f (1,..., 1, П k +1,..., П n). (1.24) Здесь a 1,..., a 2, …, ak+ 1,..., an представляют собой численные значения рассматриваемых величин в первоначальной системе единиц измерения. Значения П, П k+ 1,..., П n имеют нулевую размерность относительно единиц измерения А 1, А 2,..., Аk , т.е. являются безразмерными. Это видно, например, из того, что размерность величины ak+ 1 (dim ak+ 1 = Полученный результат известен, как отмечено выше, под названием П-теоремы (или π –теоремы) Бэкингема. Смысл ее заключается в том, что если n величин связаны между собой функциональной зависимостью и из них k величин являются основными (т.е. имеют независимые размерности), то из этих величин можно образовать n – k безразмерных комбинаций. Чем меньше число n – k, тем определеннее становится решение задачи. При n – k = 1 решение задачи, как правило, становится однозначным. Из общего числа величин можно выделить ту, которая более всего интересует, и выразить ее в виде явной функции в зависимости от остальных. Иначе говоря, различные соотношения между размерными величинами можно выразить как соотношения между безразмерными величинами. В этом и заключается существо применения метода теории размерностей для исследования закономерностей в механике. Ранее отмечалось, что выбор числа основных единиц осуществляется произвольно. Число основных единиц в системе измерений механических величин можно довести до одной, например, на базе единицы длины. Единица времени Т в этом случае будет производной величиной, которая отражает время, в течение которого свет проходит в вакууме путь, равный единице длины L. Однако на практике такая система неудобна, так как различные производные величины и размерные коэффициенты, число которых уменьшается с уменьшением числа основных единиц, в определяющих уравнениях будут иметь одну и ту же размерность. С увеличением числа основных единиц увеличивается число размерных коэффициентов. При построении систем единиц измерения, как показала практика, следует подбирать и физические величины, и число основных единиц так, чтобы в определяющих уравнениях было возможно меньше размерных коэффициентов. На практике наиболее удобной оказалась Международная система единиц физических величин с семью основными и двумя дополнительными единицами измерения. Увеличение числа основных единиц измерения полезно только в том случае, когда из дополнительных физических условий ясно, что физические постоянные, возникающие при введении новых основных единиц измерения, являются несущественными. Например, при рассмотрении механических и тепловых процессов при измерении количеств теплоты и механической энергии можно ввести две основные единицы измерения – калорию и джоуль соответственно. В этом случае возникает физическая размерная постоянная (коэффициент) J, которая называется механическим эквивалентом теплоты.
Однако в процессе теплопередачи в движущейся несжимаемой идеальной жидкости взаимного превращения тепла в механическую энергию или обратно не происходит. Поэтому тепловые и механические процессы и величины, их характеризующие, следует рассматривать независимыми друг от друга. Даже если бы была возможность изменять значения механического эквивалента J, это не сказалось бы на значениях производных величин, т.е. величина J не вошла бы в физические соотношения между размерными величинами. В этом случае увеличение числа основных единиц измерения позволило бы получить дополнительную информацию. Из сказанного выше можно заключить: 1. Число аргументов в искомой зависимости(1.22), записанной в безразмерном виде(1.24),сокращается на число, равное числу определяющих параметров с независимыми размерностями. 2. Анализ размерностей в общем не дает способа однозначного решения уравнения (1.24) в зависимости от n – k аргументов. Для окончательного установления зависимости (1.24) следует обращаться либо к эксперименту, либо к математической теории решения задачи. При k = n решение практически однозначно. 3. Первоначальным и основным этапом в постановке и решении задач является схематизация процесса. Схематизация и определение существенных и несущественных параметров представляют наибольшие трудности при применении анализа размерностей для решения задач. Методы исследования различных задач механики, физики, астрофизики, геофизики, природных и экологических явлений, основанные на применении анализа размерностей и подобия, дополняют современные методы исследования фундаментальных естественно-научных закономерностей. При применении анализа размерностей трудность заключается не в использовании методики получения закономерностей физических явлений в наиболее простой и наглядной форме, а в схематизации физического явления, процесса. Здесь следует находить основные параметры задачи, выделяемые при математической постановке задачи в виде соответствующих дифференциальных уравнений с начальными и краевыми условиями. Тем самым упрощается нахождение искомой зависимости, выражающей физическую закономерность. Эти выводы будут проиллюстрированы в последующих примерах.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.137.164 (0.037 с.) |
 = Lp Mq+yT – 2 y .
= Lp Mq+yT – 2 y . . Из этого следует, что время не зависит от удлинения пружины a.
. Из этого следует, что время не зависит от удлинения пружины a. S
S  , где, как и в первой задаче, С – безразмерный и неопределяемый коэффициент пропорциональности; p, q, r, k, l – подлежащие определению показатели степени.
, где, как и в первой задаче, С – безразмерный и неопределяемый коэффициент пропорциональности; p, q, r, k, l – подлежащие определению показатели степени.
 .
. .
. .
.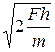 , т.е. C =
, т.е. C =  .
. k
k  = С
= С  .
. 
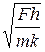 .
. (1.22)
(1.22)
 ;
;
 (1.23)
(1.23) ), являющейся числителем П k+ 1, совпадает с произведением размерностей величин, входящих в знаменатель.
), являющейся числителем П k+ 1, совпадает с произведением размерностей величин, входящих в знаменатель.


