
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика формулы размерности
Зависимость производных величин от основных физических величин (точно так же в отношении их единиц измерения) может быть представлена, как показано выше, в виде формулы. Эта формула называется формулой размерности, и ее можно рассматривать как емкое определение и характеристику физической природы производной величины. Размерность следует соотносить с определенной системой физических величин или системой единиц измерения физических величин. Такой вывод следует из того, что для одной и той же величины в разных системах единиц измерения формула размерности может содержать различное число сомножителей (аргументов) и иметь различный вид. В системе единиц величин, например CGS (единицы измерения: сантиметр, грамм, секунда), формулы размерности всех физических величин имеют вид произведения степенных сомножителей: dim x = LαM β T γ. Такой вид формулы размерности следует из физического условия: отношение двух численных значений любой производной величины не должно зависеть от выбранных масштабов для основных величин (или для единиц основных величин). Например, значение отношения двух площадей, измеренных в квадратных метрах, будет равно значению отношения этих же площадей, измеренных в квадратных дециметрах (сантиметрах, гектарах, километрах и т.д.). Данное утверждение можно легко доказать в общем виде. Допустим, имеется производная размерная величина y, являющейся функцией аргументов, в качестве которых могут выступать различные величины: механические, теплотехнические, световые и т. д. Для упрощения их можно рассматривать как геометрические. Тогда существующие связи между этой размерной величиной и длинами (расстояниями) в общем виде можно представить в виде уравнения y = f (x1, x2 ,..., x n), где x 1, x 2 ,..., xn – некоторые линейные величины. Обозначим через y 1значение величины y, которое соответствует значениям аргументов x
Это означает, что значение y 1/ y должно быть одинаковым при любом значении единицы измерения или масштаба длин α. Из приведенного выше равенства (1.1) получаем
Тогда значение y = f (x1, x2 ,..., x n), зависящее от первоначально принятой единицы измерения (единичной меры), можно записать как y (1), а значение размерной величины y 1 = f (x1a, x2a, ..., xna) – как y 1(1), а выражение (1.2) как
Здесь a – произвольно выбранное числовое значение масштаба измеряемой величины (кратная или дольная единица измерения). Величина, обозначаемая буквой φ, представляет собой числовое значение отношений значений измеряемой величины для заданного значения a. В зависимости от a получается множество φ, в котором эти величины функционально связаны. Таким образом, в уравнении (1.3) величины y (a), y (1), y 1(a) и y 1(1) не являются константами в принятом понимании, а представляют собой обобщенный индивидуальный параметр. Такое понятие является одним из центральных в теории размерностей и в теории подобия. Отсюда следует, что отношение числовых значений геометрической величины, измеренной в разных масштабах величин, зависит только от отношения масштабов величин (в данном случае длин). Из последнего соотношения нетрудно найти вид функции φ(a). Так как на основании соотношения (3)
где a 1, a 2 , – произвольно выбранные масштабы измерения величин или соотношения применяемых единиц измерения Так как при x
Отсюда с учетом уравнения (1.4) и (1.5) следует
с последующим преобразованием уравнения (1.6) φ(a 1) = φ(a 2) Продифференцируем уравнение (1.7) по a 1:
Так как выбор масштаба а произволен, то уравнение (1.8) будет справедливо при а 1 = а 2 = а = 1. В этом случае это уравнение можно переписать в виде
Здесь m – значение правой части уравнения (1.9) без сомножителя Разделяя переменные и интегрируя данное уравнение, найдем Этот вывод справедлив для любой размерной величины, зависящей от нескольких основных величин, если меняется только один масштаб. Очевидно, если меняются масштабы a, β, γ трех основных величин, то функция φ будет иметь вид φ(a, β, γ) = am β n γ t.
Рассмотренное доказательство представления уравнения в виде произведения степенных сомножителей дано в общем виде. Приведем доказательства этого положения на основе конкретного примера определения размерности силы. Два тела одинаковой массы в течение некоторого времени подвергаются действию разных сил F 1 и F 2. Начальные скорости обоих тел равны нулю. Тела проходят разные расстояния l 1 и l 2. Так как массы тел и время движения в обоих случаях одинаковы, то силы и пройденные расстояния будут функционально связаны. Принимаем единицу длины в качестве основной, а единицу силы – производной, т. е. зависящей от единицы длины. Зависимости сил от пройденного расстояния можно записать в общем виде: F 1 = f (l 1) и F 2 = f (l 2). Из условия абсолютного значения относительных количеств вытекает, что отношение F 1/ F 2 = f (l 1)/ f (l 2) не зависит от выбора единицы длины. Единицу длины можно изменять (уменьшать или увеличивать) в любое число раз. Если ее уменьшить в x раз, то численные значения измеренных расстояний пройденных телами, увеличатся в x раз, т. е. F 1/ F 2 = f (x l 1)/ f (x l 2) = f (l 1)/ f (l 2). Это уравнение можно переписать в таком виде: f (xl 1) = [ f (l 1)/ f (l 2)] f (xl 2). Продифференцируем обе части этого уравнения по x:
l 1 Так как число x выбрано произвольно, то уравнение (1.10) должно быть справедливым и при x = 1. Тогда это уравнение можно переписать в следующем виде:
Это равенство должно выполняться при любых l. Поэтому
Можно изменить условие задачи и определить численные значения двух сил, под действием которых два тела разной массы за одно и тоже время пройдут одинаковые расстояния. Повторив предыдущие рассуждения, приходим к результату f (m) = K 2 mb. Точно так же для двух тел равной массы, прошедших равные расстояния за разные промежутки времени, получим f (t) = K 2 tc. Общую зависимость можно представить в виде f (l, m, t) = K lambtc, (1.11) здесь коэффициент K является числом, не зависящим от выбора единиц физических величин. Этим доказывается, что формулы размерности физических величин должны иметь вид степенных сомножителей. Следует отметить, что закономерности, связывающие между собой физические величины, могут выражаться неалгебраическими функциями: тригонометрическими, показательными, логарифмическими, эвольвентными и другими неалгебраическими уравнениями. Из соотношения (1.11) следует, что изменение единиц измерения величин, входящих в аргументы соответствующих функций, не должно изменять единиц измерения зависимых величин. Это возможно при условии образования ими безразмерных комбинаций, которые не изменяются при любом изменении единиц измерения величин, принятых в качестве основных при образовании систем измерения. Например зависимость силы тока I разряда конденсатора емкостью С от времени t имеет экспоненциальный характер:
I = Для того чтобы это равенство сохранялось при любом выборе единиц измерения физических величин, следует показатель степени (– t / RC) представить безразмерным. Это ведет к необходимости представления произведения RC (сопротивления и емкости) в знаменателе с размерностью времени. В физике это произведение получило название «постоянная времени контура. Если единицу емкости и сопротивления рассматривать в качестве основных (независимых) единиц измерения, то в показатель степени кроме указанных величин должна войти размерная постоянная величина. Подобное имеет место в формуле, выражающей зависимость барометрического давления p от высоты точки измерения:
p = p 0 где p 0 – давление на уровне поверхности моря; m – масса молекулы; g – ускорение свободного падения; kБ – постоянная Больцмана; T – температура.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.233.150 (0.011 с.) |
 ; x
; x  ;..., x
;..., x  . Числовое значение y, а также y 1, зависит от единицы измерения длины, принятой для линейных величин (длин) x 1, x 2 ,..., xn. Изменим эту единицу измерения или масштаб длин в α раз. То числовые значения y, соответствующие этим линейным величинам, изменятся также в α раз. Согласно сформулированному выше условию должно иметь место равенство соотношений
. Числовое значение y, а также y 1, зависит от единицы измерения длины, принятой для линейных величин (длин) x 1, x 2 ,..., xn. Изменим эту единицу измерения или масштаб длин в α раз. То числовые значения y, соответствующие этим линейным величинам, изменятся также в α раз. Согласно сформулированному выше условию должно иметь место равенство соотношений =
=  (1.1)
(1.1) . (1.2)
. (1.2) (1.3)
(1.3) ,
,  , то отсюда следует
, то отсюда следует , (1.4)
, (1.4) = x 1
= x 1  , x
, x  = x 2 a 2,..., x
= x 2 a 2,..., x  (1.5)
(1.5) (1.6)
(1.6) = φ(a 2)
= φ(a 2) 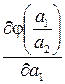
 . (1.8)
. (1.8) =
= 
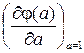 =
=  · m. (1.9)
· m. (1.9) . Так как при
. Так как при  имеем
имеем  , то постоянная интегрирования С = 1; следовательно,
, то постоянная интегрирования С = 1; следовательно,  .
. =
=  l 2
l 2  . (1.10)
. (1.10) =
=  .
. = а, где а – некоторая постоянная величина. Разделяя переменные и интегрируя, получим f (l) = K 1 la .
= а, где а – некоторая постоянная величина. Разделяя переменные и интегрируя, получим f (l) = K 1 la . .
. ,
,


