
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрологические возможности эффекта МессбауэраСодержание книги
Поиск на нашем сайте
Как известно, радиоактивный распад ядер сопровождается тремя видами излучения (α-излучение, β-излучение, γ-излучение), которые имеют разную природу. Эффект Мессбауэра связан с γ-излучением, представляющем собой коротковолновое электромагнитное излучение с длиной волны λ < 10–10м. Вследствие малой длины волны данный вид излучения рассматривается в виде потока квантов энергии. Дискретность (квантованность) энергии излучения обусловливает линейчатый характер его спектра. Прохождение γ-излучения через вещества сопровождается целым рядом физических эффектов: фотоэффектом, комптоновским рассеянием излучения с изменением длины волны, образованием электронно-позитронных пар в электрическом поле и другими физическими явлениями. Волновой характер излучения обусловливает возможность возникновения резонансных эффектов. Ядро вещества, находящееся в основном состоянии, поглощает γ-квант энергии и переходит в возбужденное состояние. В возбужденном состоянии ядро находится недолго и переходит вновь в основное, испуская γ-квант энергии. Для стадий испускания и поглощения γ-квантов энергии требуется точное соответствие по их величине, т.е. попадание поглощаемого γ-кванта энергии в резонанс с энергетическим состоянием ядра. Так как излучаемые ядром кванты энергии распространяются в любом направлении, двухстадийный процесс поглощения-излучения носит название резонансного рассеивания γ-излучения. Такая картина резонансного поглощения γ-квантов представлялась только теоретической, так как при излучении γ-кванта имеет место динамическая отдача ядра, связанная с поглощением некоторой энергии. В результате величины поглощаемого и излучаемого γ-квантов неодинаковы: E γ = E ур – E я, где Eγ – энергия излученного γ-кванта; E ур – энергия ядра в возбужденном состоянии после поглощения γ-кванта (энергию основного состояния ядра условно можно считать равной нулю); E я – кинетическая энергия отдачи ядра. Из-за явления отдачи ядра считалось, что резонансное рассеяние γ-квантов практически не может наблюдаться. При возбуждении ядра, находящегося в основном состоянии, энергия поглощенного кванта должна иметь величину E погл = E γ – E я = E ур – 2 E я < E ур. Вместе с тем точного равенства между E погл и E ур в соответствии с принципом соотношения неопределенностей Гейзенберга не требуется. Неопределенность E ур, т.е. некоторый разброс в уровне энергии ∆ E, называемый шириной уровня и обозначаемый буквой Г, равен Г ≈ h/τ. Такой разброс в величине энергии допускается как при поглощении, так и при испускании γ-квантов для наблюдения у них эффекта резонансного рассеяния. Например, возбужденное состояние ядра изотопа иридия 191Ir имеет энергию Еур = 129 кэВ в течение τ ≈ 10–10 с. Отсюда следует, что Г ≈ 4 · 10–5 эВ. Энергия отдачи ядра в соответствии с законом сохранения импульса энергии равна Е я = р я2/2 m я = р γ2/2 m я = Е γ2/2 m я с 2 ≈ Е 2/2 m я с 2 ≈ 0,05 эВ. Энергия отдачи ядра на три порядка больше ширины уровня Г. Из этого следует, что резонансное рассеяние γ-квантов на спектре поглощения наблюдать практически невозможно. В действительности следует учитывать дополнительные явления. Ядра участвуют в тепловом движении, колеблясь около положения равновесия. Направление испускания γ-квантов может совпадать с направлением колебаний, а может быть противоположным ему. Такое явление, известное в оптике и акустике, называется эффектом Доплера. Этот эффект способствует разбросу энергий испускаемых и поглощаемых γ-квантов около среднего значения. Этот интервал разброса энергий может значительно превышать ширину уровня Г. Расширение линии D спектра энергий поглощения или испускания за счет эффекта Доплера при комнатной температуре достигает 0,07 эВ. Это значение сравнимо с энергией отдачи ядра ЕЯ. Поэтому кривые распределения вероятностей энергий испускания и поглощения γ-квантов частично перекрываются, в результате чего часть γ-квантов может испытывать резонансное рассеяние (рис. 5.25). На рис. 5.25 пунктирные кривые соответствуют теоретическим распределениям значений энергий возбужденного ядра (кривая 1), поглощенного γ-кванта (кривая 2) и испускаемого γ-кванта (кривая 3) в отсутствие эффекта Доплера. На кривой 2 учтена энергия отдачи ядра при поглощении γ-кванта, а на кривой 3 учтены энергии отдачи ядра при поглощении и испускании γ-кванта. Из-за эффекта Доплера области под кривыми расширяются и частично перекрывают друг друга. Отношение этой общей площади к площади под одной из кривых соответствует доле γ-квантов, которые могут испытать резонансное рассеяние. Мессбауэр в своих исследованиях охлаждением источника γ-квантов и их рассеивателя решил устранить влияние эффекта Доплера и сократить число резонансно-рассеянных γ-квантов. Эффект оказался противоположным, так как число резонансно-рассеянных γ-квантов значительно увеличилось. Объяснение этому явлению Мессбауэр связал с тем, что импульс и энергия отдачи при низкой температуре передаются не отдельному ядру, а всей кристаллической решетке в целом. Так как микрообъем кристалла имеет гораздо большую массу по сравнению с массой ядра, то энергия отдачи конечного объема кристалла в соответствии с формулой Е 2/2 m я с 2 будет пренебрежимо малой. Процессы поглощения и испускания γ-квантов атомными ядрами происходят практически без потерь энергии, т.е. идеально упруго. Явление упругого испускания или поглощения γ-квантов атомными ядрами твердого тела без изменения его внутренней энергии называется эффектом Мессбауэра. Правильность объяснения данного явления была подтверждена другим экспериментом, схема которого представлена на рис.5.26. В этом опыте источник γ-квантов мог изменять скорость своего перемещения относительно рассеивателя методом кругового вращения. При окружной скорости 0,02–0,03 м/с из-за эффекта Доплера резонансное рассеивание исчезало. При такой скорости движения изменение энергии γ-квантов составило 5 · 10–6 эВ. Таким образом, в этом эксперименте была непосредственно измерена ширина энергетического уровня ядра, которая составляет 1/ 25 000 000 000 часть энергии перехода ядра в возбужденное состояние (E ур = 129 кэВ). На основании эффекта Мессбауэра экспериментальная физика приобрела метод измерений физических величин с чрезвычайно высокой точностью. Например, частота излучения квантов может быть измерена с точностью Г /Е = 10 –15 – 10–17. Высокая точность измерения частоты позволила скорость света в вакууме принять в качестве фундаментальной физической константы.
Эффект Ааронова–Бома
Эффект по своей физической сущности представляет собой интерференционный квантовомеханический эффект непрямого действия поля на заряженную частицу. Он наблюдается при воздействии внешнего электромагнитного поля на заряженную частицу, траектория которой находится вне области сосредоточения данного поля. Данная схема действия магнитного поля на движущийся электрический заряд отличается от классического взаимодействия поля и заряда с возникновением силы Лоренца. В эффекте Ааронова–Бома сила Лоренца не возникает и не может рассматриваться из-за отсутствия локального контакта поля и заряда. Впервые на возможность такого эффекта указали У. Эренберг и Р. Сайди в 1949 г. Независимо друг от друга подробное теоретическое обоснование эффекта проведено в 1959 г. Я. Аароновым и Д. Бомом. Они раскрыли тесную связь этого явления с фундаментальными положениями квантовой теории электромагнитного излучения на основе свойств электромагнитных потенциалов поля. Эксперимент Ааронова–Бома (рис.5.27) был задуман для того, чтобы доказать влияние магнитного потенциала на электронную интерференцию при отсутствии магнитного поля. Эксперимент заключался в установке магнитной нити или тонкого соленоида между электронными траекториями, идущими из двух виртуальных когерентных источников. Продольная ось нити или соленоида была перпендикулярна к проекциям траекторий на линию, соединяющую источник излучения частиц и фокус их схождения (S, F). Длина нити или соленоида была достаточной для того, чтобы магнитное поле, исходящее от их концов, не могло изменять электронные траектории. Раздвоенные с помощью бипризмы Френеля–Меленстеда и экрана когерентные потоки заряженных частиц обтекали магнитную нить или соленоид радиусом R с двух сторон и сходились в фокусе F. Возможность эффекта формально обусловлена тем, что в уравнение Шредингера для волновой функции заряженной частицы во внешнем электромагнитном поле входит выражение для магнитного потенциала этого поля. Волновой вектор электрона в магнитном потенциале А, даже если магнитное поле равно нулю, описывается формулой де Бройля:
здесь h – постоянная Планка; λ – длина волны де Бройля; m – масса заряженной частицы; n – целое число; ν – частота колебаний; e – множитель; Магнитный потенциал определяет фазу волновой функции и при правильном выборе геометрических параметров и точной настройке опытной установки приводит к наблюдаемому интерференционному эффекту даже при отсутствии прямого силового воздействия поля на частицу. Этот эффект не зависит от выбора калибровки потенциалов для определения начала отсчета при проведении измерений и обусловлен разницей фаз вдоль различных возможных путей распространения частицы. Огибающие соленоид потоки заряженных частиц испытывают сдвиг фаз в противоположных направлениях. Он существует как для скалярного, так и для векторного потенциала электромагнитного поля. Для того чтобы магнитный поток Ф был сосредоточен внутри нити или соленоида, линии магнитной индукции должны быть бесконечно длинными, это предполагается в теоретических вычислениях. Но на практике длина нити или соленоида может быть равна нескольким миллиметрам, так как их поперечные размеры находятся в пределах нескольких микрометров. Соленоид (или магнитная нить) окружен непроницаемым для частиц цилиндрическим экраном радиуса R 0 > R. В этом случае волновая функция частицы целиком сосредоточена в области, где магнитное поле отсутствует и только векторный потенциал A отличен от нуля на основании теоремы Стокса (интеграл берется по контуру L, охватывающему соленоид). Поэтому сила Лоренца на заряженную частицу не действует, но амплитуда расходящейся цилиндрической волны оказывается зависящей от потока магнитного поля. Она содержит два члена, один из которых, описывающий амплитуду рассеяния заряженных частиц на экранирующей поверхности, исчезает в предельном рассмотрении. Второй член, не зависящий от R 0, определяет амплитуду рассеяния заряженных частиц в эффекте Ааронова–Бома. Этой же формулой описывается амплитуда рассеяния заряженных частиц на соленоиде без защитного экрана для предельного случая изменения его диаметра (R = 0) с заданным магнитным потоком Ф. Формула не точна в области малых углов расхождения потоков частиц. Точный расчет свидетельствует о появлении тени за рассеивателем, причем коэффициент ослабления амплитуды падающей плоской волны равен Х. Особенностью рассеяния в эффекте Ааронова–Бома является исчезновение рассеянной волны, если магнитный поток в соленоиде равен целому числу (n) квантов потока (Ф = n Ф0). В этом случае точная волновая функция отличается от волновой функции свободной частицы лишь калибровочным множителем, и такое магнитное поле не влияет на квантовое состояние частицы. Условие отсутствия рассеяния в эффекте Ааронова–Бома совпадает с условием квантования Дирака для магнитных зарядов. Эксперименты по наблюдению эффекта Ааронова – Бома при рассеянии электронов магнитным полем проводились начиная с 60-х гг. XX в. Пучок монохроматических электронов разделялся на два когерентных потока, обтекавших рассеиватель – тонкую нить (диаметром до 1 мкм) из магнитного материала или миниатюрный соленоид (диаметром равным ~ 14 мкм), магнитным потоком которого можно было управлять. Затем когерентные пучки вновь соединялись, образуя интерференционную картину, зависящую от величины охватываемого магнитного потока, в достаточном согласии с теоретическим расчетом эффекта Аaронова–Бома. Экспериментальная схема эффекта Ааронова-Бома, представленная на Однако при анализе этих экспериментов необходимо учитывать искажения интерференционной картины, вызванные рассеянным магнитным полем, возникающим из-за неоднородного намагничивания нити и конечных продольных размеров рассеивателя. Современные эксперименты с тороидальными магнитами, а также со сверхпроводящими квантовыми интерферометрами, свободными от этих недостатков, надежно подтверждают существование эффекта Аaронова–Бома. Перспективы широкого применения эффекта Ааронова–Бома в метрологии достаточно высокие при создании надежных стандартных приборов и инструментов.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.29 (0.009 с.) |

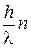 = hk = mv + eA,
= hk = mv + eA,


