
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Релятивистская физическая картина мира
Теория Максвелла, основанная на системе математических уравнений в интегральной и дифференциальной форме, предполагает, что все величины в пространстве и времени изменяются непрерывно. Этими величинами являются электрические заряды и токи. Теория позволила объяснить не только известные результаты экспериментов, но и предсказать новые явления. Таким выводом явилось предположение о существовании токов смещения, единственным свойством которых является, в отличие от токов проводимости, создание в окружающем пространстве магнитного поля. Создание магнитного поля током проводимости связано с движением в проводнике электрических зарядов. Создание магнитного поля током смещения связано только с изменением электрического поля во времени. Название «ток смещения» является данью истории науки, так как по сути это изменяющееся во времени электрическое поле. Предвидение наличия магнитного поля у токов смещения позволило Максвеллу предсказать существование переменного электромагнитного поля, т.е. электромагнитных волн, распространяющихся в пространстве с определенной скоростью. Как было установлено позднее, скорость свободного распространения электромагнитных волн в вакууме равна скорости света С и составляет 3 · 108 м/с. Этот результат и теоретический анализ свойств электромагнитных волн привели к созданию электромагнитной теории света. Экспериментально электромагнитная природа света была подтверждена Г. Герцем. Однако создание Максвеллом своей теории вызвало появление несоответствия ее выводов механической картине мира. Классическая механика, базирующаяся на первом законе Ньютона, в Евклидовом пространстве (с прямоугольной системой координат) допускала инвариантность преобразования координат при переходе из одной системы (X, Y, Z) в другую (x ', y ', z '). Например, преобразования координат x ' = x – vt; y ' = y; z ' = z не ведут к изменению формы уравнений движения по отношению к этим преобразованиям. Инвариантность уравнений движения в отношении к этим преобразованиям называют принципом Галилея. Преобразования Галилея, описывающие переход от одной инерциальной системы отсчета S к другой S ' и наоборот, имеют следующий вид: S
Схема преобразований представлена на рис. 3.1.
Уравнения Максвелла относительно преобразований Галилея оказались неинвариантны, т.е. к электромагнитным процессам галилеевский принцип относительности не может быть применен. Здесь потребовалось новая механика, которая представляла бы классическую механику как предельный случай для малых скоростей движения материальной точки (v << c). Это было создано в теории относительности на основе работ А.Пуанкаре, Г. Лоренца, А.Эйнштейна, Кэли и других физиков с привлечением аппарата неевклидовой геометрии. Теорию относительности современные физики называют теорией инвариантов четырехмерной области пространства–времени относительно некоторой группы преобразований. Простейшим является преобразование Галилея. Ниже будет раскрыто содержание преобразования Лоренца для электромагнитной теории. Теория относительности соответствует определенной проективной системе координат при изучении обобщенной геометрии взаимодействия физических объектов. В основе специальной теории относительности лежат постулаты Эйнштейна: – все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой (никакие опыты не дают возможности обнаружить покой или равномерное прямолинейное движение системы отсчета); – скорость света в вакууме инвариантна во всех инерциальных системах отсчета. Эйнштейн показал, что в теории относительности преобразования Галилея, описывающие переход от одной инерциальной системы отсчета S к другой S 1 и наоборот, заменяются преобразованиями Лоренца, которые имеют следующий вид: S
где β = v/ c. Здесь S и S' – инерционные системы отсчета; x, y, z и x ', y ', z ' – координаты в системах отсчета; v – скорость движения систем отсчета относительно друг друга; t и t ' – время в системах отсчета; с – скорость света; β– соотношение скоростей движения инерциальной системы С относительно системы С ' и света. Из преобразования Лоренца вытекают очень важные для метрологии выводы: 1. В движущейся инерциальной системе время замедляется по сравнению с неподвижной системой (эффект замедления хода часов подтвержден экспериментально).
2. В движущейся инерциальной системе линейные размеры сокращаются тем больше, чем больше скорость движения, в соответствии с формулой
где 3. Скорость света в вакууме есть предельная скорость, которую невозможно превысить. В дальнейшем, используя результаты работ О. Хэвисайда, Г. А. Лоренца, А.Пуанкаре и других физиков, А. Эйнштейн сделал достоянием научной общественности физическую зависимость между полной энергией движущегося тела Е и его массой m: E = m c2 = В правой части данного выражения в числителе дана энергия покоя тела массой m 0. В классической механике энергия покоя практически равна нулю и не учитывается, так как для небольших скоростей соотношение v 2 / c2 имеет пренебрежимо малое значение. Однако при больших скоростях это соотношение следует учитывать, что важно для современной метрологии. Неевклидовы геометрии При создании общей теории относительности Эйнштейн использовал неевклидовы геометрии, т.е. геометрии пространств, имеющих в отличие от евклидового пространства кривизну. Первооткрывателями неевклидовой геометрии следует назвать профессора Казанского университета Н.И. Лобачевского и немецкого математика Г.Ф. Римана. Основные идеи новой неевклидовой геометрии Лобачевский изложил на заседании физико-математического отделения Казанского университета 23 февраля 1826 г. Результаты развития этих идей он опубликовал в 1829 г. в «Казанском вестнике» в статье «О началах геометрии». В 1835 г. в «Ученых записках Казанского университета» были представлены основные положения его новой теории под названием «Воображаемая геометрия». В этом же году эта работа была издана в Германии. Почти такие же результаты были изложены венгерским математиком Яношем Бойяи в 1832 г. Геометрия Римана была представлена позднее почти на 30 лет. Евклидова геометрия основывается на одном из главных постулатов: из точки вне прямой можно провести только одну прямую, параллельную данной. Из него логически вытекает вывод равенства суммы углов треугольника 180°, или двум прямым углам, теорема Пифагора (квадрат гипотенузы равен сумме квадратов катетов) и ряд других геометрических теорем. В геометрии Лобачевского через точку вне данной прямой можно провести множество прямых, не пересекающихся с данной прямой, а сумма углов треугольника меньше суммы двух прямых углов. В геометрии Римана через точку вне прямой нельзя провести ни одной не пересекающейся с ней прямой, а сумма углов треугольника больше двух прямых углов. Кроме того, перпендикуляры к одной и той же прямой сходятся (в геометрии Лобачевского они расходятся). Таким образом, в этих геометриях имеет место иное определение мер (метрика), чем в геометрии Евклида. Нетрудно показать, если плоскость искривляется и становится поверхностью сферы, то теоремы Евклида переходят в теоремы геометрии Римана. Евклидова геометрия поверхности при более сложном искривлении плоскости переходит в геометрию Лобачевского. Понять сущность геометрий Римана и Лобачевского можно, обращаясь к их моделям, хотя и не совсем точным. Геометрия Римана представляет собой эллиптическое пространство, которое для наглядности удобнее рассмотреть на сферической модели, например Земного шара (рис. 3.2). На сфере меридианы перпендикулярны к экватору. В евклидовой геометрии две прямые линии, перпендикулярные к рассматриваемой, будут параллельными, но на сфере такие линии (меридианы) пересекаются на Северном и Южном полюсах. Неевклидовы геометрии различаются по сумме углов треугольника. Отклонения суммы углов треугольника от 180°.
Эти отклонения наглядно можно показать с помощью модели поверхности сферы. На рис.3.2 треугольник NAB образован дугами двух меридианов и экватором. Два угла у экватора содержат по 90°. Добавление угла у Северного полюса делает сумму углов больше, чем 180°. Если передвинуть меридианы так, чтобы они пересекались под прямым углом, то сумма всех углов составит 270°, так как каждый из них равен 90°. Следует отметить различие между сферической моделью и римановым пространством. В римановом пространстве две прямые линии на плоскости имеют только одну общую точку, в то время как линии на сфере, которые соответствуют прямым линиям (наибольшие окружности), всегда пересекаются в двух точках. Сферическая модель будет соответствовать римановой плоскости только тогда, когда рассматривается только часть поверхности сферы, которая не содержит точек, подобных Северному и Южному полюсам, т.е. пары противоположных точек. С помощью сферической модели можно легко увидеть, что в римановом пространстве отношение длины окружности к ее диаметру всегда меньше π (рис.3.3). На рис.3.3 показан сегмент сферы (Земли) с вершиной N (Северным полюсом) и с центром основания С. Сегмент соответствует поверхности в римановом пространстве. В качестве радиуса сегмента можно рассматривать не отрезок СВ, так как он не лежит на сферической поверхности, а дугу NB. В качестве диаметра следует рассматривать дугу ANB. Отношение длины окружности на срезе сегмента к длине дуги ANB будет меньше значения π, так как длина дуги ANB (диаметр в римановом пространстве) меньше длины отрезка AСB (диаметр в евклидовом пространстве). Пространство Лобачевского в сравнении с римановым пространством имеет обратную кривизну. Модель поверхности в пространстве Лобачевского (рис.3.4) наглядно можно представить в виде седловины между двумя горными вершинами (переносицы носа, поясницы лошади и т.д.). Окружность в евклидовом пространстве будет соответствовать замкнутой волнистой линии в пространстве Лобачевского, которая образуется наложением на седловину круга определенного диаметра из легко растягивающейся ткани. На рис.3.4 длина каждой из кривых GCE и FCD будут равна диаметру окружности круга в евклидовом пространстве.
Для того чтобы достигнуть плотного прилегания ткани к поверхности седловины на четырех участках волнистой линии, образуемой кромками круга, эту ткань следует растянуть. Другими словами, увеличить длину волнистой линии в сравнении с длиной окружности круга в евклидовом пространстве. Отсюда следует, что отношение длины волнистой линии к длине диаметра FCD будет больше значения π. Более точная модель в пространстве Лобачевского (рис. 3.5) может быть построена вращением некоторой кривой AB – трактрисывокруг оси CD (лат. tractus – вытянутый). Эта кривая обладает тем свойством, что отрезок ее касательной в любой точке от точки касания до определенной прямой имеет одну и ту же длину. Трактриса иначе называется кривой погони. Любой треугольник на этой вогнутой поверхности будет иметь в отличие от плоского треугольника сумму углов меньше 180°. Все поверхности, как евклидовы, так и неевклидовы имеют в любой их точке свойство, называемое кривизной этой поверхности в данной точке. Геометрия Лобачевского характеризуется тем, что любая точка ее поверхности имеет отрицательную кривизну с постоянным значением. Существует бесконечное множество геометрий Лобачевского, поверхности каждой из которых характеризуются фиксированным параметром свойства – отрицательным числом, мерой кривизны. Для евклидовой геометрии кривизну плоскости можно представить как дугу с бесконечным радиусом. Следует иметь в виду следующее обстоятельство. Точка поверхности образуется пересечением двух прямых, кривизна каждой из которых может быть разной и с противоположным знаком. В этом случае кривизна поверхности рассматривается как обратная величина произведения радиусов кривых. В седловине (геометрия Лобачевского) один радиус будет положительный, а другой отрицательный и соответственно значение кривизны поверхности будет оставаться отрицательным. Для поверхностей Евклида кривизна поверхности равна нулю. Для геометрии Римана кривизна сферической (эллиптической) поверхности всегда будет положительной, независимо от того, с какой стороны она будет рассматриваться, так как произведение отрицательных радиусов имеет положительное значение. Из анализа параметров поверхностей неевклидовых геометрий вытекает, что кривизна как свойство отличается от общепринятого термина «кривизна» в евклидовом пространстве, так как обе стороны неевклидовой поверхности равнозначны. Позднее Риман разработал обобщенную неевклидову геометрию, в которой геометрии Евклида, Римана и Лобачевского представляют ее частные случаи. Для наглядности отдельные параметры названных геометрий приведены в табл. 3.1. Среди этих пространств находится и пространство Эйнштейна, принимаемое в его общей теории относительности. Таблица 3.1
|
||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.01 с.) |
 S ' S '
S ' S '  S
S
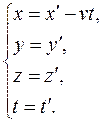
 S 1
S 1 
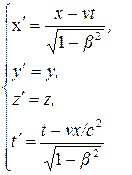

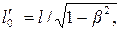
 – линейный размер тела в движущейся системе; l – линейный размер тела в неподвижной системе.
– линейный размер тела в движущейся системе; l – линейный размер тела в неподвижной системе.



