
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результативность производстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание темы
1. Эволюция теоретических подходов к понятию «производственная функция» 2. Производственная функция «Кобба-Дугласа» 3. Линейная производственная функция 4. Производственная функция Леонтьева
1. Эволюция теоретических подходов к понятию «производственная функция»
Считается, что современная теория производства сложилась в конце XIX – начале XX вв. В 1890 г. производственная функция как зависимость выпуска от количества применяемых ресурсов в явном виде была представлена английским математиком А. Берри, который помогал А. Маршаллу при подготовке математического приложения к его «Принципам экономической науки».[1] Первые попытки установить зависимость выпуска от количества применяемых ресурсов и дать ей какое-то аналитическое выражение имели место еще до нашей эры. Например, в трактате «О земледелии» известный римский писатель и государственный деятель Марк Порций Катон (234-149 гг. до н. э.) описывает две образцовые виллы: оливковую виллу и винодельческое хозяйство. Среди множества рекомендаций по их обустройству есть и такие: для обработки оливковой рощи в 240 югеров (1 югер равен примерно 3 тыс. м2) Катон определяет необходимое число рабов в 13 человек, включая вилика (управляющего) и вилику (ключницу), а для обработки виноградника в 100 югеров это число составляет 16 человек. Нормы, предложенные Катоном, вызвали возражение у Марка Теренция Варрона (116 – 27 гг. до н. э.) и отражены в его трактате «О сельском хозяйстве». Варрон не соглашается, что между площадью участка и числом рабов, необходимых для его обработки, существует прямая пропорциональная зависимость. Варрон отмечал, что в общее число рабов Катон не должен был включать вилика и вилику, т.е. расходы по управлению, т.к. эти расходы постоянны и не зависят от площади участка. Варрон пришел к выводу, что количество рабов будет зависеть и от естественных условий отдельных участков. Кроме того, он, по сути дела, говорил о необходимости сопоставления затрат и выпуска как приращений соответствующих переменных. Определенный вклад в развитие понятия производственных функций внес и Н.Г. Чернышевский. Он так определил задачу экономической науки: «Разложив продукт на доли, соответствующие разным элементам производства, она должна искать, какое сочетание этих элементов и долей дает наивыгоднейший практический результат. В чем тут состоит задача – понятно каждому: надобно отыскать, при каком сочетании элементов производства данное количество производительных сил дает наибольший продукт».[2] Н.Г. Чернышевский предложил производственную функцию,[3] показывающую зависимость производства от двух факторов: А ∙ В = С, где А – «производительные орудия»; В – «работник»; С – «количество продукта известных качеств, производимого дневным трудом этого работника посредством этих орудий». Коэффициенты при А, В и С характеризуют, соответственно, «степень достоинства» орудий и работника и «успешность производства». К. Маркс, в свою очередь, взаимосвязь между количествами применяемых ресурсов и объемом выпуска называл техническим строением капитала. Он писал, что техническое строение капитала «покоится на техническом базисе и на известной ступени развития производительных сил может рассматриваться как данное. Требуется определенная масса рабочей силы, представленная определенным числом рабочих, чтобы произвести определенную массу продукта, например, в течение одного дня, и, следовательно, - что уже при этом, само собой разумеется, - привести в движение, потребить производительно определенную массу средств производства, машин, сырья и т.д. Отношение это очень различно в различных отраслях производства, часто даже в различных подразделениях одной и той же отрасли промышленности, хотя, с другой стороны, в очень отдаленных друг от друга отраслях промышленности оно случайно может быть совершенно или почти одинаковым».[4] В 1871 г. в Санкт-Петербурге вышла небольшая книга Н. Огроновича, в которой была сформулирована идея производственной функции. Автор пишет: «Труд мой «Наука о концентрировании атомов, индивидов, ферм»… будет по преимуществу не социальный, а политико-экономический, ибо в основу войдет математическая функция, найденная для определения производства; из этой функции мы можем определить maximum и minimum функции, или наибольшее и наименьшее производство всякого организма индивидуального, всякого организма фермы и всякого другого организма. Потом будет определена ценность из этой функции всякой производительной силы, которая есть не что иное, как прибыль или как d -л производства этой производительной силы, помноженной на то число, какое будет показывать, сколько раз производительная сила участвовала в производстве общем в данный момент производства». [5] Таким образом, Н. Огронович задолго до работ П. Дугласа пришел к идее производственной функции.
2. Производственная функция «Кобба-Дугласа»
Существует широкий выбор формул, которые можно использовать для представления производственных функций. Производственная функция показывает зависимость между количеством используемых факторов производства и максимально возможным при этом выпуском продукции. 1. Наиболее популярна производственная функция Кобба – Дугласа. Макроэкономическая производственная функция описывает статистически значимую связь между совокупным выпуском (доходом) Y и различными видами затрат или объемами используемых ресурсов. Простейшая производственная функция Кобба – Дугласа, примененная в анализе экономики США в 20-30-х гг. прошлого века, имеет вид:
где A – коэффициент, характеризующий эффективность производства, α и β – коэффициенты эластичности по капиталу (K) и труду (L) соответственно, которые согласно классической теории отражают роль каждого фактора производства в приросте конечного продукта или долю дохода соответствующего фактора в единице совокупного дохода. В результате расчёта с помощью метода наименьших квадратов при условии, что а+ß = 1, было установлено, что за исследуемый период значение А равно 1,01, a - ¼, ß - ¾, отсюда функция приняла следующий вид:
Для графического представления производственной функции длинного периода в двухмерном пространстве используют семейство линий равного выпуска. Линия равного выпуска, или изокванта, представляет множество различных сочетаний объемов труда и капитала, при которых достигается один и тот же объем выпуска. Рисунок 1.1 – Изокванта
Дальнейшее развитие этой функции пошло в направлении введения фактора времени, отражающего процесс перехода от статической модели Кобба – Дугласа типа Y =F(K, L) к динамической функции Y =F(K, L, t) с учётом влияния технического прогресса на объём производимой продукции. В итоге функция Кобба - Дугласа приобрела следующий обобщённый вид:
где ert – фактор, отражающий влияние качественных изменений в производстве, в т. ч. технического прогресса. Особенность этой функции в том, что r выступает в ней как комплексный показатель роста совокупной экономической эффективности всех факторов производства. Этот показатель помимо изменений в технике отражает улучшение качества и повышение эффективности использования овеществлённого или живого труда, а также ряд других факторов. Так, Я. Тинберген, изучив динамику объёма производства, капитала, занятых и технических изменений для четырёх стран - Германии, Великобритании, Франции и США - за 1870-1914 гг., получил следующие результаты (при том условии, что в качестве параметров α и ß были взяты доли капитала и труда в национальном доходе – соответственно, ¼ и ¾): в Германии экстенсивные факторы - увеличение затрат капитала и труда - обеспечили 60 % роста, технический прогресс - 40 %; в Великобритании - соответственно 80 и 20 %; в США - 73 и 27 %. Для оценки влияния экономических факторов на макроэкономическую динамику мы поставили перед собой задачу построения производственной функции для России. Для этого были собраны следующие данные: объем ВВП (Y), инвестиции в основной капитал (K), начисленная заработная плата всех занятых в экономике России (L) за период 2001 – I квартал 2008 годов. В качестве переменной Y взят ВВП, в качестве L – среднемесячная заработная плата всех занятых в экономике России. Заработная плата в России до сих пор остается главной составляющей в структуре доходов и ее динамика отражает структурные изменения в потреблении. В качестве K рассматриваются инвестиции в основной капитал, являющиеся важным показателем сферы накопления. При оценке производственной функции по имеющимся данным необходимо использовать метод последовательных разностей для устранения тенденции и сглаживания сезонных колебаний. Можно ожидать, что отдача от масштаба этой функции будет возрастающей. Для построения производственной функции использовалась модель с нейтральным НТП (1), так как она отражает выявленные связи между показателями и позволяет исследовать влияние НТП на прирост ВВП (Y). Производственная функция России (в приростах за квартал) за период 2001 – 2008 годов по нашим расчетам имеет следующий вид (1.3) в приростах за квартал:
при этом R2=0,925 – коэффициент детерминации, DW=2,35 – статистика Дарбина-Уотсона. Последние годы влияние инвестиций в основной капитал и оплаты труда на макроэкономическую динамику России несколько изменилось. Динамика ВВП по-прежнему зависит от изменения инвестиций с лагом 1 год, но влияние капитала стало более существенным, чем в период 1996 – 2005 годов. Большее влияние на макроэкономическую динамику России оказывает оплата труда с лагом 1 квартал и 3 квартала. Влияние НТП остается несущественным.
3. Линейная производственная функция
Линейная производственная функция имеет вид:
т.е. это коэффициенты, представляющие предельную производительность факторов. Изокванта для линейной производственной функции будет иметь следующий вид: Рисунок 1.2 – Изокванта для линейной производственной функции Прямая изокванта иллюстрирует случай совершенной взаимозаменяемости факторов производства, когда для замены единицы капитала требуется 1,4 ед. труда независимо от количества используемого труда и капитала.
4. Производственная функция Леонтьева
Производственная функция, отображающая технологию с использованием взаимодополняемых факторов производства, называется производственной функцией Леонтьева. Она имеет следующий вид:
Изокванта для производственной функции Леонтьева будет иметь следующий вид: Рисунок 1.3 – Изокванта для функции Леонтьева
Прямоугольная изокванта Y=20 представляет технологию с жестко взаимодополняемыми факторами: при уменьшении труда или капитала на единицу 20 ед. продукции уже произвести нельзя, как ни увеличивай объем использования второго фактора. С другой стороны, сколько ни добавляй труда к объему капитала, выпуск не увеличивается В современном обществе важную роль играет система образования, внедрение современных информационных технологий, развитие средств транспорта и связи, углубление специализации, совершенствование управления предприятиями. Конкурентоспособность страны на мировом рынке определяется уже не столько дешевизной рабочей силы, сколько качеством труда, уровнем образования работников, их способностью осваивать новые технологические процессы, качеством менеджмента. Современные экономисты неоклассического направления, используя аппарат производственных функций в сочетании с другими методами моделирования, эконометрики и статистики, делают попытку оценить влияние всех перечисленных факторов на экономический рост, повышение производительности труда.
5. Предельная норма технического замещения
Предельная норма технического замещения одного фактора другим, например капитала трудом (MRTSl,K), показывает на какую величину следует изменить количество одного фактора (капитала, ΔK) при изменении количества другого фактора (труда) на одну единицу (ΔL), чтобы размеры выпуска не изменились. Иными словами, Или в дифференциальной форме:
Чтобы при изменении количества используемых факторов производства выпуск оставался неизменным, количества труда и капитала должны изменяться в разных направлениях. Если количество капитала сокращается ΔK <0, то количество труда должно увеличиваться ΔL>0. Поэтому отношение ΔK/ ΔL(Qconst) всегда отрицательное. Между тем, предельная норма технического замещения представляет собой просто пропорцию, в которой один фактор производства может быть замещен другим, и является величиной положительной (MRTSl,K>0). Отсюда следует, что MRTSl,K равна соотношению ΔK/ ΔL(Qconst), взятому с обратным знаком. MRTSl,K определяется соотношением предельных продуктов труда MPL и капитала MPK. Вспомним, что предельный продукт фактора производства характеризует изменение выпуска при изменении количества данного фактора на одну единицу и при неизменном количестве других факторов. Соответственно, MPL = ΔQ/ ΔL; MPK = ΔQ/ΔK или в дифференциальной форме: MPL = dQ/dL; MPK = dQ/dK. Можно доказать, что MRTSl,K = MPL/ MPK. (1) Когда мы изменяем затраты труда на ΔL, выпуск изменяется ΔL· MPL, когда же изменяем затраты капитала на ΔK, выпуск изменяется на ΔK· MPK. Поскольку определение MRTS предполагает, что общий выпуск при изменении затрат труда и капитала остается неизменным, можно записать: ΔL· MPL + ΔK· MPK = 0, отсюда ΔK· MPK = - ΔL· MPL или – ΔK/ ΔL = MPL/ MPK, что и доказывает справедливость выражения (1). MRTS может быть интерпретирована как численное выражение тангенса угла наклона изокванты ΔK/ ΔL. Величина и динамика MRTS характеризуют степень взаимозаменяемости факторов производства. Важной характеристикой производственной функции является показатель эластичности замещения. Коэффициент эластичности δ показывает, насколько процентов должна измениться капиталовооруженность труда, т.е. соотношение между капиталом и трудом, чтобы при неизменном выпуске предельная норма технического замещения изменилась на один процент:
или в дифференциальной форме:
Поскольку вдоль каждой изокванты отношения K/L и MRTS меняются в одном и том же направлении, снижаются при увеличении количества труда в способах производства и возрастают при увеличении капитала, показатель δ всегда положителен. Он может варьироваться от бесконечности (для линейной производственной функции) до нуля (для леонтьевской функции). Данный коэффициент позволяет соизмерять степень взаимозаменяемости ресурсов для различных производственных процессов.
Контрольные вопросы
1. Способы описания технологий: производственное множество, производственная функция и множество необходимых факторов производства. 2. Свойства производственных множеств. 3. Агрегирование в теории производства. 4. Виды производственных функций, используемых в экономическом анализе и прогнозировании и их свойства. 5. Понятие эластичности замены одного ресурса другим. 6. Производственная функция с постоянной эластичностью замены ресурсов и ее связь с производственной функцией Кобба-Дугласа, линейной и производственной функцией Леонтьева. 7. Учет в производственной функции научно-технического прогресса в экзогенной и эндогенной формах. Задачи к теме 1 Задача 1 Необходимо определить предельную производительность капитала и труда и предельную норму технологического замещения капитала трудом, если технология характеризуется линейной производственной функцией следующего вида: y = 5*K + 7*L. Решение MPK = MPL = MRTSKL =
Задача 2 Конкурентная фирма имеет общие затраты TC = Q2 + 20Q + 800. Она получает в краткосрочном периоде максимально возможную прибыль, равную 800. Необходимо определить цену на рынке и объем выпуска данной фирмы.
Задача 3 Необходимо определить предельную производительность капитала и труда и предельную норму технологического замещения труда капиталом и капитала трудом, если технология характеризуется линейной производственной функцией следующего вида: y = 2*K + 5*L.
Задача 4 Функция общих издержек конкурентной фирмы описывается уравнением ТС = 0,5Q3 – 20Q2 + 1600Q + 2000. При каком уровне цены фирма прекратит производство и уйдет с рынка?
Задача 5 Конкурентная фирма имеет общие затраты TC = 2Q2 + 40Q + 800. Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000. Необходимо определить цену на рынке и объем выпуска данной фирмы.
Задача 6 Производственная функция конкурентной максимизирующей прибыль фирмы задана выражением Q = 10K0,5L0,5. Цена единицы труда равна цене единицы капитала и составляет 4 тыс. руб. Определите цену единицы выпуска.
Задача 7 Производственная функция конкурентной фирмы имеет вид а) определите комбинацию ресурсов (K*;L*), максимизирующую выпуск фирмы при лимите затрат на ресурсы; б) определите объем максимального выпуска ymax(K*;L*); в) напишите уравнение изокванты, проходящей через точку (K*;L*); г) постройте точку (K*;L*) на графике. Постройте по трем точкам изокосту; д) постройте по трем точкам изокванту.
Задача 8 Производственная функция конкурентной фирмы имеет вид вид а) определите комбинацию ресурсов (K*;L*), минимизирующую издержки фирмы при фиксированном объеме выпуска y0 = 4; б) определите минимальные издержки фирмы Cmin(K*;L*); в) напишите уравнение изокосты; г) постройте точку (K*;L*) на графике. Постройте по трем точкам изокосту; д) постройте по трем точкам изокванту. Тесты к теме 1
1. Взаимосвязь между всеми возможными вариантами сочетаний факторов производства и объемом выпускаемой продукции выражается при помощи: а) кривой производственных возможностей б) производственной функции в) эластичности предложения г) кривой общих затрат
2. Предельную норму технологического замещения капитала трудом (MRTSKL) можно определить по формуле: а)
б)
в)
г) 3. Если фирма увеличивает затраты на ресурсы на 10%, а объем производства при этом возрастает на 15%, то в этом случае: а) наблюдается отрицательный эффект масштаба б) наблюдается положительный эффект масштаба в) действует закон убывающей производительности г) кривая АТС сдвигается вверх
4. Если технология описывается производственной функцией Леонтьева, то ресурсы (капитал и труд) в ней: а) совершенно взаимозаменяемы б) взаимозаменяемы, но не совершенно (с убывающей предельной нормой технологического замещения) в) жестко взаимодополняемы г) нет верного ответа
5. Какая из следующих кривых никогда не принимает U – образной формы: а) AVC б) MC в) AFC г) ATC
6. В долгосрочном периоде: а) переменные издержки растут быстрее, чем постоянные б) все издержки являются переменными в) все издержки являются постоянными г) постоянные издержки растут быстрее, чем переменные
7. Постоянные издержки – это: а) затраты на зарплату управляющего персонала, охраны, % по кредитам, амортизацию оборудования б) затраты на зарплату рабочих, охраны, стоимость сырья и оборудования в) затраты на оплату труда работников, амортизацию оборудования, рентные платежи г) затраты на сырье, электроэнергию, ренту, % по кредиту
8. Общие экономические издержки на всю массу производимой продукции (ТС) зависят от объема выпуска следующим образом: TC = 0,1Q3 – 4Q2 + 50Q + 100. Тогда функция средних переменных издержек (AVC) имеет вид: а) AVC = 100 б) AVC = 0,3Q2 – 8Q + 50 в) AVC = 0,1Q2 – 4Q + 50 г) AVC = 0,1Q3 – 4Q2 + 50Q
9. Средние общие издержки производства продукции (АТС) достигают минимума при том объеме выпуска, когда: а) AVC = FC б) P = MC в) MC = AVC г) MC = ATC
10. В краткосрочном периоде фирма производит 500 единиц продукции. Средние переменные издержки (AVC) составляют 2 руб., средние постоянные издержки (ATC) равны 0,5 руб. Общие издержки (ТС) составят: а) 2,5 руб. б) 1250 руб. в) 750 руб. г) невозможно определить на основе имеющихся данных
11. В производственной функции Кобба-Дугласа (Y = AKtα Ltβ), коэффициенты α и β обозначают: а) предельную производительность капитала и труда б) среднюю производительность капитала и труда в) эластичность выпуска по капиталу и труду г) предельную норму технологического замещения капитала трудом и наоборот
12. Множество различных сочетаний объемов труда и капитала, при которых достигается один и тот же объем выпуска, отображается на графике: а) изоквантой б) изокостой в) изобарой г) изопрофитой
13. Технология, для которой характерна совершенная взаимозаменяемость факторов производства, описывается: а) производственной функцией Кобба – Дугласа б) производственной функцией Леонтьева в) линейной производственной функцией г) вообще не может быть описана производственной функцией
14. Эластичность замещения труда капиталом характеризует: а) отдачу от использования труда б) отдачу от использования капитала в) взаимозаменяемость труда и капитала в производственном процессе г) отдачу от масштаба
15. Для производственной функции Кобба – Дугласа вида: Y = 1,01 Kt0,25 Lt0,75 характерен: а) положительный (растущий) эффект масштаба б) отрицательный (снижающийся) эффект масштаба в) постоянный эффект маштаба г) недостаточно данных для ответа на вопрос
16. В производственной функции Леонтьева вида: Y = min {a1 K; a2 L}, коэффициенты a1 и a2 обозначают: а) предельную производительность капитала и труда б) среднюю производительность капитала и труда в) эластичность выпуска по капиталу и труду г) предельную норму технологического замещения капитала трудом и наоборот
17. Для линейной производственной функции вида: Y = 4K + 5L предельная производительность капитала равна: а) 4 б) 5 в) 4/5 г) 5/4
18. Для линейной производственной функции вида: Y = 4K + 5L предельная норма технологического замещения капитала трудом равна: а) 4 б) 9 в) 4/5 г) 5/4
19. Современные экономисты – неоклассики используют аппарат производственных функций: а) для централизованного планирования объемов производства в национальной экономике б) для расчета ВВП и других показателей СНС в) для оценки влияния различных факторов на экономический рост г) все перечисленные выше ответы верны
20. Для какой производственной функции (ПФ) характерна изокванта следующего вида:
а) ПФ Кобба – Дугласа б) ПФ Леонтьева в) линейной ПФ г) изокванта не может иметь такой вид
21. Функция Кобба – Дугласа вида Y = AKtα Ltβ ert, в отличие от функции вида Y = AKtα Ltβ: а) является нелинейной б) не может быть рассчитана на реальных статистических данных в) учитывает влияние научно-технического прогресса на динамику ВВП г) не учитывает влияние капитала на динамику ВВП
22. В краткосрочном периоде фирма-совершенный конкурент будет получать положительную прибыль, если: а) Цена продукта выше минимума средних общих издержек. б) Цена продукта ниже переменных издержек. в) Цена продукта ниже минимума средних переменных издержек. г) Цена продукта ниже предельных издержек.
23. Если технология производства характеризуется производственной функцией Леонтьева вида Y = min {4K; 5L}, и фирма использует 20 ед. капитала и 10 ед. труда, то объем выпуска фирмы составит: а) 80 ед. б) 50 ед. в) 130 ед. г) 30 ед.
24. Задача вида: Y = Kα Lβ → max rK + wL = C0 K,L ≥ 0 предполагает: а) максимизацию выпуска при фиксированном уровне затрат на факторы производства б) максимизацию затрат на производство при фиксированном уровне выпуска в) минимизацию выпуска при фиксированном уровне затрат на производство г) минимизацию затрат на производство при фиксированном уровне выпуска
25. Какие из следующих издержек не принимаются во внимание при выработке решений об оптимальном объеме производства фирмы? а) средние переменные издержки б) неявные издержки в) средние постоянные издержки г) предельные издержки 26. Современная теория производства сложилась а) в конце XVIII – начале XIX вв. б) в конце XIX – начале XX вв. в) в конце XX в. г) нет верного ответа. 27. Производственная функция – это: а) зависимость между количеством труда и капитала, используемым для производства фиксированного количества продукции; б) зависимость между количеством используемых факторов производства и максимально возможным при этом выпуском продукции; в) зависимость между количеством используемых факторов производства и выпуском продукции, позволяющим получить максимальную прибыль; г) зависимость между количеством используемых факторов производства и затратами фирмы на них.
28. Соотнесите графики изоквант и названия типов производственных функций (ПФ).
а) ПФ Кобба-Дугласа; б) ПФ Леонтьева; в) Линейная ПФ.
29. Простейшая производственная функция Кобба – Дугласа имеет вид:
а) коэффициенты, характеризующие эффективность производства; б) коэффициенты эластичности по капиталу и труду; в) предельные производительности капитала и труда; г) предельные нормы технологического замещения труда капиталом и капитала трудом.
30. Линейная производственная функция отражает: а) совершенную взаимозаменяемость факторов производства; б) жесткую взаимодополняемость факторов производства; в) недостаток факторов производства; г) избыток факторов производства.
31. Линейная производственная функция имеет вид: а) коэффициенты, характеризующие эффективность производства; б) коэффициенты эластичности по капиталу и труду; в) предельные производительности капитала и труда; г) предельные нормы технологического замещения труда капиталом и капитала трудом.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.0.67 (0.028 с.) |

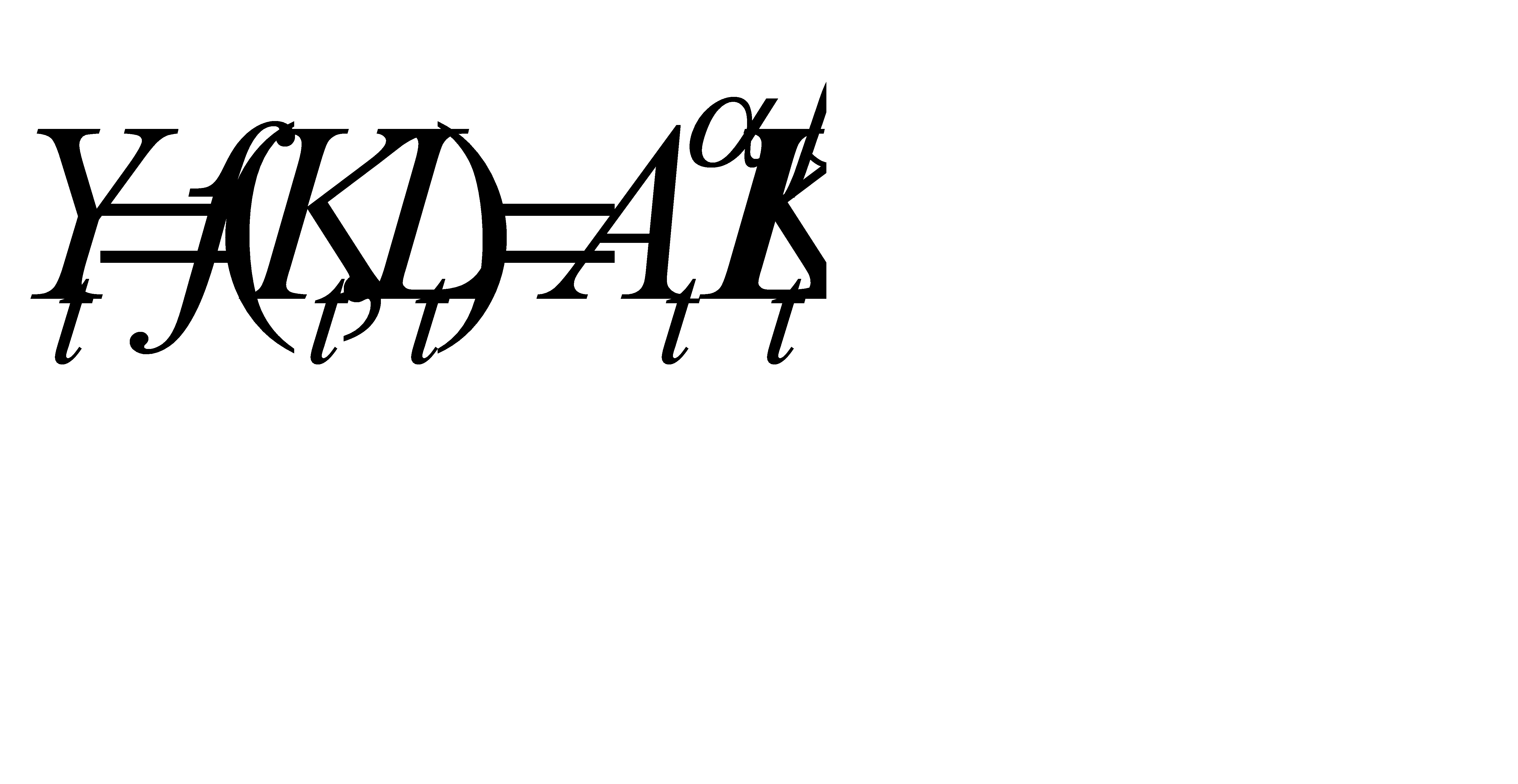 , (1.1)
, (1.1) . Из неё следует, что самым важным фактором производства является труд, т. к. созданная им доля составила 3/4 всего объёма производства и 1 % увеличения затрат труда расширяет объём производства в 3 раза больше, чем 1 % прироста капитала. Функция показывает также, что прирост объёма производства происходит медленнее, чем прирост затрат каждого из факторов: при росте на 1 % затрат труда объём производства практически возрастёт на ¾, а при увеличении на 1 % затрат капитала – на ¼.
. Из неё следует, что самым важным фактором производства является труд, т. к. созданная им доля составила 3/4 всего объёма производства и 1 % увеличения затрат труда расширяет объём производства в 3 раза больше, чем 1 % прироста капитала. Функция показывает также, что прирост объёма производства происходит медленнее, чем прирост затрат каждого из факторов: при росте на 1 % затрат труда объём производства практически возрастёт на ¾, а при увеличении на 1 % затрат капитала – на ¼. ;
; 
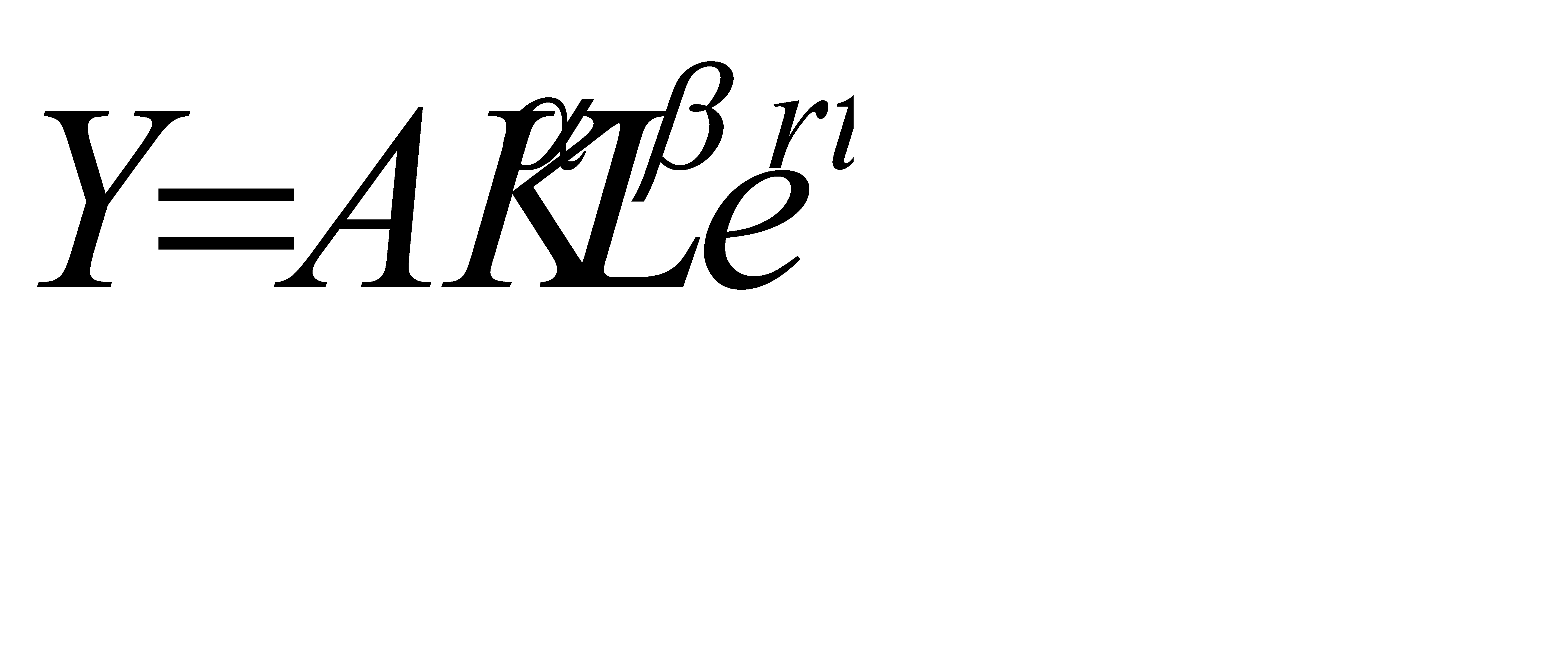 , (1.2)
, (1.2) , (1.3)
, (1.3)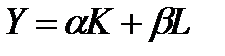 , где
, где  ,
,  , (1.4)
, (1.4) , где
, где 

 (1.5)
(1.5) (1.6)
(1.6)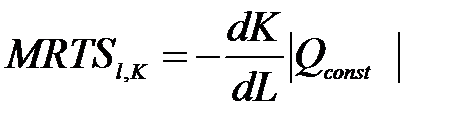 (1.7)
(1.7) (1.8)
(1.8)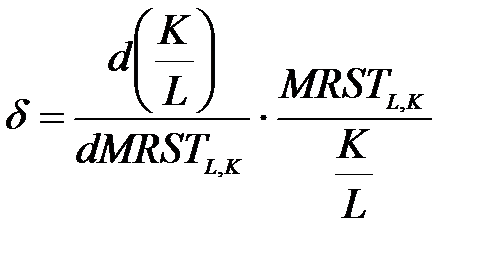 (1.9)
(1.9)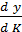 = 5 – предельная производительность капитала;
= 5 – предельная производительность капитала;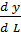 = 7 – предельная производительность труда;
= 7 – предельная производительность труда;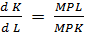 =
=  = 1,4 - предельная норма технологического замещения капитала трудом.
= 1,4 - предельная норма технологического замещения капитала трудом. (K – количество капитала, L – количество труда). Цены капитала и труда соответственно равны r = 4 и w = 5. Лимит затрат на ресурсы равен C0 = 120:
(K – количество капитала, L – количество труда). Цены капитала и труда соответственно равны r = 4 и w = 5. Лимит затрат на ресурсы равен C0 = 120: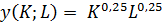 (K – количество капитала, L – количество труда). Фиксированный выпуск фирмы y0 = 4. Цены на капитал и труд соответственно равны r = 16 и w = 4:
(K – количество капитала, L – количество труда). Фиксированный выпуск фирмы y0 = 4. Цены на капитал и труд соответственно равны r = 16 и w = 4: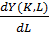

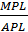

 , где α и β – это:
, где α и β – это:


