Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Теория поведения потребителяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание темы
1. Потребительские предпочтения 2. Максимизация функции полезности при бюджетном ограничении методом Лагранжа
1. Потребительские предпочтения
Теория потребления изучает поведение потребителя на рынке. Потребитель характеризуется функцией полезности и доходом, который он готов потратить на приобретение продуктов. А рынок – потребительскими наборами и ценами (ценой на единицу каждого продукта). Все величины имеют одну и ту же временную «привязку». Они постоянны в течение некоторого фиксированного периода времени (само время предполагается дискретным). Относительно способности индивида количественно оценивать, хотя бы только для себя, полезность приобретаемых им благ высказывается сомнение. В связи с этим была разработана модель поведения потребителя, основанная на гипотезах порядкового измерения полезности (удовлетворенности) индивида. Имеются следующие гипотезы в отношении потребительских предпочтений: 1. Гипотеза ненасыщения При прочих равных условиях потребитель предпочитает большее количество данного блага меньшему его количеству. 2. Гипотеза полной упорядоченности При наличии двух различных наборов благ потребитель всегда предпочитает один из них другому или признает их равноценными (одинаково предпочтительными). 3. Гипотеза транзитивности Если потребитель предпочитает набор A набору B, а набор B набору C, то он предпочитает набор A набору C. Соответственно, если набор A для потребителя равнозначен набору B и набор B равнозначен набору C, то наборы A и C тоже для него равнозначны. Гипотеза транзитивности позволяет однозначно расставить в определенной последовательности (проранжировать) всевозможные сочетания благ независимо от очередности их попарного сравнения. 4. Гипотеза рефлексивности При наличии двух одинаковых наборов благ потребитель считает, что любой из них не хуже другого. Потребительские предпочтения удобно описывать, используя кривые безразличия. Кривая безразличия – совокупность точек в пространстве двух благ, представляющих равнозначные для потребителя комбинации различных количеств обоих благ. Одна из проблем использования кривых безразличия для описания предпочтений состоит в том, что указанные кривые показывают лишь наборы, которые потребитель воспринимает как безразличные друг другу, не показывая при этом, какие наборы лучше, а какие хуже. Свойства кривых безразличия 1. Кривые безразличия имеют отрицательный наклон
Рисунок 2.1 – Кривая безразличия
1. Любой набор товаров из квадранта I предпочтительнее набора A. 2. Набор A предпочтительнее любого набора из квадранта III. 3. Все наборы товаров, имеющие равный с набором A уровень полезности должны лежать в квадрантах II и IV, т.е. кривая безразличия имеет отрицательный наклон. 2. Две кривые безразличия не могут пересекаться.
Рисунок 2.2 – Пересечение кривых безразличия
Если бы они пересекались, то наборы A, B и C были бы безразличны друг другу, а, следовательно, не могли бы лежать на отличных друг от друга кривых безразличия. Предельная норма замещения Наличие множества равнозначных для потребителя сочетаний различных количеств двух благ означает, что для него эти блага в определенной мере взаимозаменяемы. Количественной характеристикой такой взаимозаменяемости является предельная норма замещения. Предельная норма замещения блага Y благом X (MRSXY) показывает, насколько можно сократить потребление блага Y при увеличении потребления блага X на единицу, не изменяя степень удовлетворения потребителя.
Кривые безразличия для «совершенных субститутов» характеризуются тем, что MRS постоянна и равна –1. Случай «безразличных благ» – тем, что MRS везде бесконечна. Предпочтения для случая «совершенных комплементов» - тем, что MRS равна либо нулю, либо бесконечности, но не принимает никаких промежуточных значений. Для строго выпуклых кривых безразличия MRS – наклон кривой безразличия – по мере увеличения X убывает (по абсолютной величине). Таким образом, кривые безразличия демонстрируют убывание предельной нормы замещения. Это означает, что норма, по которой индивид готов заместить Y на X понижается по мере увеличения количества X.
2. Максимизация функции полезности при бюджетном ограничении методом Лагранжа
Рассмотрим задачу 1. Потребитель ведет себя рационально, если он максимизирует функцию полезности при бюджетном ограничении. Поведение потребителя может быть описано в: - вербальной форме (максимизация полезности, если хватит содержимого кошелька); - в аналитической форме (в виде задачи на условный максимум):
и в геометрической форме:
Рисунок 2.3 – Максимизация функции полезности при бюджетном ограничении
Рассмотрим линии безразличия L1 и L2, которые имеют общие точки с бюджетной прямой. Двигаясь по линиям безразличия вправо вверх, выбираем линию безразличия L2, которая имеет с бюджетной прямой точку касания (X1*, X2*). Это означает, что потребитель выбирает потребительский набор (X1*, X2*), который называется локальным рыночным равновесием потребителя. При этом функция полезности U(X1,X2) достигает своего условного максимума U*. При этом рис. 2.1 демонстрирует, что U(X1*, X2*)> U(X1',X2'), где (X1',X2') – любая точка бюджетной прямой, отличная от точки (X1*, X2*). Представленные на рис. 2.1 линии безразличия являются строго выпуклыми к точке О, это значит, что точка (X1*, X2*) ее касания с бюджетной прямой является единственной. Рассмотрим задачу 2. Потребитель достиг определенного уровня полезности U(X1,X2)=U*. Как выйти на этот уровень полезности с наименьшими расходами? (Вербальная форма задачи минимизации расхода при фиксированном уровне полезности). Аналитическая форма задачи минимизации расхода потребителя при фиксированном уровне полезности имеет вид задачи на условный минимум:
Геометрическая форма задачи минимизации расхода потребителя при фиксированном уровне полезности представлена на рис. 2.4.
Рисунок 2.4 - Минимизации расходов при фиксированном уровне полезности
По бюджетным линиям следует идти вниз до упора. Упор будет в точке касания (X1*, X2*) бюджетной прямой и линии безразличия L1. Задачи 1 и 2 называют совместными. Их можно обобщить в виде пары задач. Задача 1:
Задача 2:
Для задач 1 и 2 на условный экстремум функция Лагранжа имеет следующий вид:
Выпишем условия первого порядка локального экстремума функции:
Получили систему из трех уравнений с тремя неизвестными X1,X2,λ. Решение системы называется критической точкой функции Лагранжа (X1*,X2*, λ*). Контрольные вопросы 1. Понятие предпочтений и полезности. 2. Аксиомы выявленных предпочтений. 3. Содержание прямой и обратной задачи оптимизации индивидуального спроса. 4. Понятие двойственности в теории потребителя. 5. Характеристика взаимосвязи функций полезности, потребительских расходов и косвенной функции полезности. 6. Измерение изменений в благосостоянии потребителя: компенсирующая вариация, эквивалентная вариация и потребительский излишек. 7. Проблема агрегирования: от индивидуального выбора к совокупному спросу. Агрегированная функция спроса по группе потребителей и по группе благ.
Задачи к теме 2
Задача 1 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=2x0,5y0,5, где х, у— объемы благ. Цены благ: Рx = 4, Рy = 5, доход потребителя I = 80. Решение Имеем задачу математического программирования:
Решим ее методом Лагранжа. Построим функцию Лагранжа:
Найдем частные производные функции Лагранжа по всем переменным и приравняем их к нулю.
Решим полученную систему уравнений. Из уравнений (1) и (2) выразим
Так как левые части уравнений (1) и (2) одинаковы, значит, их правые части равны. Приравняем:
Домножим обе части уравнения на
Полученное выражение (4) подставим вместо y в уравнение (3).
Из (4) найдем y. Отсюда решение:
оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода. Задача 2 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=2x0,1y0,5, где х, у — объемы благ. Цены благ: Рx = 2, Рy = 5, доход потребителя
Задача 3 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=2x0,5y0,5, где х, у — объемы благ. Цены благ: Рx = 2, Рy = 5, доход потребителя I = 40.
Задача 4 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,5y0,5, где х, у — объемы благ. Цены благ: Рx = 5, Рy = 5, доход потребителя I = 50.
Задача 5 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,5y0,1, где х, у — объемы благ. Цены благ: Рx = 2, Рy = 1, доход потребителя I = 120.
Задача 6 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,2y0,4, где х, у — объемы благ. Цены благ: Рx = 5, Рy = 5, доход потребителя I = 90.
Задача 7 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,1y0,1, где х, у — объемы благ. Цены благ: Рx = 2, Рy = 1, доход потребителя I = 100.
Задача 8 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,1y0,1, где х, у — объемы благ. Цены благ: Рx = 1, Рy = 1, доход потребителя I = 30.
Задача 9 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,2y0,2, где х, у — объемы благ. Цены благ: Рx = 1, Рy = 1, доход потребителя I = 40.
Задача 10 Необходимо найти оптимальный выбор потребителя, максимизирующего общую полезность при фиксированном уровне дохода, методом Лагранжа. Дана функция полезности: U=x0,5y0,5, где х, у — объемы благ. Цены благ: Рx = 1, Рy = 1, доход потребителя I = 60. Задача 11 Необходимо найти оптимальный выбор потребителя, минимизирующего затраты при фиксированном уровне полезности (благосостояния), методом Лагранжа. Дана функция полезности: U=2xy, где х, у— объемы благ. Цены благ: Рx = 4, Рy = 5, уровень полезности (благосостояния) U0 = 40.
Тесты к теме 2
1. Среди следующих утверждений одно является неправильным. Укажите на него: а) Каждая точка на кривой безразличия означает различную комбинацию двух благ. б) Каждая точка на бюджетной линии означает различную комбинацию двух благ. в) Все точки на бюджетной линии означают одинаковый уровень денежного дохода. г) Все точки на кривой безразличия означают одинаковый уровень денежного дохода. д) Все точки на кривой безразличия означают одинаковый уровень удовлетворения потребностей.
2. Снижение дохода потребителя графически выражается в: а) Изменении наклона бюджетной линии. б) Параллельном сдвиге бюджетной линии вправо. в) Параллельном сдвиге бюджетной линии влево. г) Параллельном сдвиге кривой безразличия вправо. д) Параллельном сдвиге кривой безразличия влево.
3. Какой из следующих перечней значений общей полезности иллюстрирует закон убывающей предельной полезности? а) 200, 300, 400, 500. б) 200, 450, 750, 1100. в) 200, 300, 350, 380. г) 200, 400, 1600, 9600. д) 200, 350, 450, 600.
4. Цена товара Х составляет 1,5 руб. Цена товара Y составляет 1 руб. Если потребитель оценивает предельную полезность товара Y в 20 ютилей и максимизирует удовлетворение от покупки товаров X и Y, тогда предельная полезность товара X должна составлять: а) 15 ютилей. б) 20 ютилей. в) 30 ютилей. г) 45 ютилей. д) В условии недостаточно информации для ответа на вопрос.
5. Положение и наклон бюджетной линии для отдельного потребителя объясняется: а) Его предпочтениями и размерами дохода. б) Только ценами покупаемых товаров. в) Предпочтениями, размерами дохода и ценами покупаемых товаров. г) Только его предпочтениями. д) Ценами покупаемых товаров и размерами дохода.
6. Предположим, что потребитель имеет доход в 10 долл. Цена товара А равна 1 долл., а цена товара В – 0,5 долл. Какая из следующих комбинаций товаров находится на бюджетной линии? а) 8А и 1В. б) 7А и 1В. в) 6А и 6В. г) 5А и 6В. д) 4А и 12В.
7. Закон убывающей предельной полезности означает, что: а) Отношение предельных полезностей к ценам на предметы роскоши меньше, чем на товары первой необходимости. б) Отношение предельных полезностей к ценам одинаково для всех товаров. в) Полезность, приносимая каждой последующей единицей товара, убывает по мере увеличения количества приобретаемых товаров. г) Полезность приобретаемых товаров убывает по мере увеличения дохода потребителя. д) Ни один из ответов не является верным.
8. Общая полезность достигает максимального значения, когда предельная полезность: а) Уменьшается. б) Увеличивается. в) Равна нулю. г) Является величиной положительной. д) Является величиной отрицательной.
9. Теория потребительского поведения предполагает, что потребитель стремится максимизировать: а) Разницу между общей и предельной полезностью. б) Среднюю полезность. в) Предельную полезность. г) Общую полезность. д) Каждую из перечисленных величин.
10. Потребительское равновесие на карте безразличия – это: а) Любое пересечение бюджетной линии и кривой безразличия. б) Та точка, в которой наклон бюджетной линии равен наклону касательной к ней кривой безразличия. в) Любая точка на самой высокой из кривых безразличия. г) Любая точка, расположенная на бюджетной линии. д) Любая точка, расположенная на пространстве, ограниченном бюджетной линией.
11. Совместите следующие карты кривых безразличия со словесными описаниями предпочтений потребителя:
11.1 11.2 11.3 а) Товары X и Y совершенно взаимозаменяемые для потребителя. б) Товары X и Y жестко взаимодополняемые для потребителя. в) Потребитель предпочитает товар X и равнодушен к товару Y. г) Потребитель предпочитает товар Y и равнодушен к товару X.
12. Функция полезности потребителя имеет вид: U(X;Y) = 3X + 5Y. Предельная норма замещения (MRS) товара Y товаром X составит: а) 3/5. б) 5/3. в) 3X + 5Y. г) 8. д) 3X.
13. Увеличение дохода потребителя графически выражается в: а) Изменении наклона бюджетной линии. б) Параллельном сдвиге бюджетной линии вправо. в) Параллельном сдвиге бюджетной линии влево. г) Параллельном сдвиге кривой безразличия вправо. д) Параллельном сдвиге кривой безразличия влево.
14. Эффект дохода имеет место в следующем случае: а) Если доходы людей падают, они покупают меньше данного продукта. б) Удешевление товаров приводит к тому, что потребитель может купить больше данного товара, не сокращая объема приобретения других товаров. в) Объем покупок некоторых товаров сокращается по мере увеличения доходов людей. г) По мере того, как доходы людей растут, они сберегают увеличивающуюся часть дохода. д) Во всех перечисленных случаях.
15. Потребитель расходует 20 долл. в неделю на покупку товаров А и В.
Чтобы получить максимальное удовлетворение, потребитель должен: а) Покупать меньше товара А и больше товара В. б) Покупать прежнее количество товара А и больше товара В. в) Покупать больше товара А и меньше товара В. г) Покупать больше товара А и прежнее количество товара В. д) Не изменять структуру покупок, так как он уже получает максимальное удовлетворение.
16. Эффект замены – это рост спроса на товар, вызванный: а) Изменением общего уровня цен на все товары. б) Изменением во вкусах потребителя, предпочитающего покупать товары-заменители. в) Изменением в реальном доходе, вызванном снижением цен на потребляемые товары. г) Предложением новых заменителей товара. д) Ни один из предыдущих ответов не является верным.
17. Общая полезность растет, когда предельная полезность: а) Уменьшается. б) Увеличивается. в) Равна нулю. г) Является величиной положительной. д) Является величиной отрицательной.
18. Предельная норма замещения товара А товаром В означает: а) Сколько единиц товара А потребитель приобретает, когда цена товара В уменьшается на 1 руб. б) В какой степени увеличивается предельная полезность, если потребление товаров А и В увеличивается на 1 единицу. в) Сколько единиц товара В потребитель покупает, когда его доход возрастает, а потребление товара А остается прежним. г) От какого количества единиц товара А потребитель готов отказаться в обмен на получение одной единицы товара В, чтобы общая полезность осталась неизменной. д) Ни один из ответов не является верным.
19. Чтобы оказаться в положении равновесия (т.е. максимизировать полезность) потребитель должен: а) Не покупать некачественных товаров. б) Быть уверенным, что цены всех приобретаемых им товаров пропорциональны общим полезностям. в) Уравновешивать предельные полезности последних единиц приобретаемых товаров. г) Быть уверенным, что цена каждого товара равна предельной полезности денег. д) Распределять доход таким образом, чтобы последний рубль, истраченный на покупку какого-либо товара, приносил такой же прирост полезности, как и рубль, истраченный на покупку другого товара.
20. Если потребитель выбирает комбинацию двух благ, представленную точкой, лежащей на плоскости, ограниченной бюджетной линией, то он: а) Максимизирует полезность. б) Желает купить больше товаров, чем позволяет его бюджет. в) Не полностью использует свой бюджет. г) Находится в положении потребительского равновесия. д) Ни один из ответов не является верным.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 862; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.136.190 (0.009 с.) |



 (2.1)
(2.1) (2.2)
(2.2)
 (2.3)
(2.3)
 (2.4)
(2.4)
 (2.5)
(2.5) (2.6)
(2.6)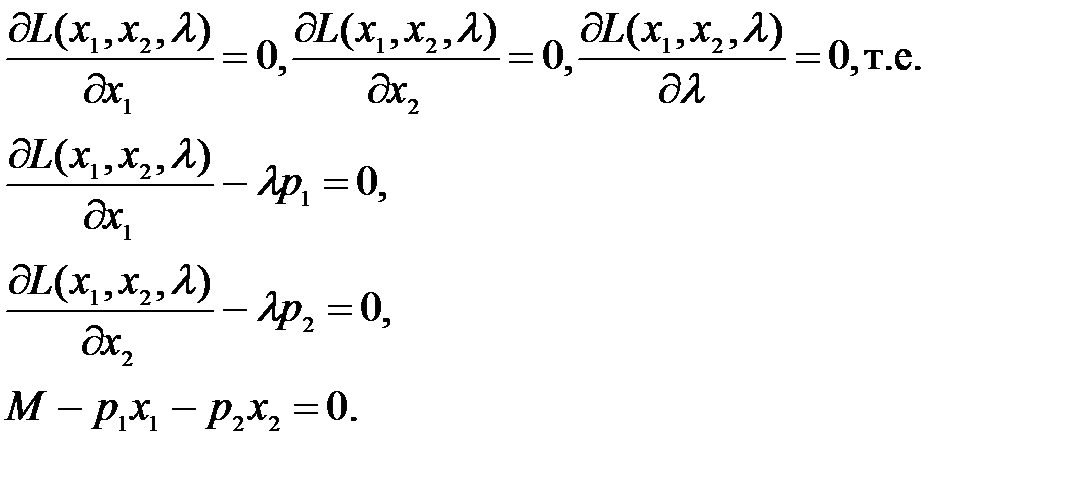 (2.7)
(2.7)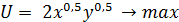
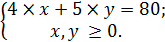

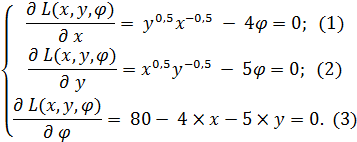
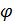 . Получим:
. Получим:
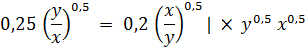
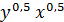 и выполним преобразования. Получим:
и выполним преобразования. Получим: