
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Общее равновесие и общественное благосостояниеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание темы
1.Понятие общего экономического равновесия 2.Простой обмен в двухсубъектной двухпродуктовой экономике 3. Коробка Эджуорта и контрактная линия
1. Понятие общего экономического равновесия
В микроэкономике используются модели двух типов – оптимизационные, для изучения отдельных экономических субъектов (потребителей, производителей, собственников ресурсов) и равновесные, для изучения взаимоотношений между экономическими субъектами (или группами их). В свою очередь равновесные модели подразделяются на модели частичного, многорынкового (англ. multimarket) и общего равновесия. Модели частичного равновесия используются для анализа отдельных, мысленно изолированных друг от друга рынков конкретных, как правило, однородных, благ и факторов производства. При этом предполагается, что на всех остальные рынки распространяется принцип «прочих равных условий». Так, можно исследовать рынок пшеницы, абстрагируясь от того, что происходит на рынках других зерновых, сельхозтехники, удобрений и т.п., или рынок услуг врачей терапевтов, абстрагируясь от того, что происходит на рынках услуг врачей других специальностей, медсестер, медицинской техники, лекарств и т.п. Во многих случаях такой подход с точки зрения частичного равновесия оказывается полезным. В случаях многорынкового равновесия целесообразно исследование рынков неоднородной продукции или ресурсов, например рынка сельхозпродукции или труда в целом. В модели общего равновесия рассматривается взаимосвязь и взаимозависимость всех образующих частей экономической системы. Рынки всех товаров и всех производственных факторов в действительности взаимосвязаны. Проблема, которую пытается разрешить теория общего равновесия, заключается в том, может ли, и каким образом, многосубъектная децентрализованная экономическая система, предполагающая свободу действий каждого индивида, обеспечить такое поведение участников, при котором окажется возможным эффективное распределение ресурсов. Общее экономическое равновесие определяется как такое состояние экономики, когда все рынки одновременно находятся в равновесии, а каждый субъект максимизирует свою целевую функцию. Теория общего равновесия обязана своим становлением Леону Вальрасу (1834-1910), который показал, что общее равновесие совместимо с такой экономической системой, в которой на каждом рынке выполняются условия совершенной конкуренции (модель общего конкурентного равновесия). Это значит, что если все покупатели и продавцы являются ценополучателями, можно найти такую систему цен, при которой все рынки будут находиться одновременно в состоянии равновесия и каждый их субъект максимизирует свою целевую функцию при данных ограничениях. В модели Вальраса общее равновесие – результат решения системы уравнений, неизвестными в которых являются цены всех благ и факторов производства и их количества, покупаемые и продаваемые каждым потребителем и производителем. Уравнения отражают максимизирующее поведение потребителей и производителей. Часть их (поведенческие уравнения) представляет функции спроса и предложения всех покупателей на всех рынках, а часть – уравнения «расчистки» рынков, т.е. их равновесия. В принципе такая система уравнений имеет решение, если количество независимых уравнений равно числу неизвестных в системе. Но это лишь необходимое условие, но не достаточное. Доказательство существования общего равновесия достаточно сложная задача, решить которую не удалось ни самому Вальрасу, ни его последователям. В реальном мире преобладают отнюдь не совершенно конкурентные рынки. Тем не менее, теория общего равновесия – весьма важный раздел микроэкономики, поскольку пытается решить задачу эффективного размещения ресурсов в экономике. Мы рассмотрим лишь наиболее простые модели общего экономического равновесия, описывающих взаимосвязь рынков в условиях совершенной конкуренции, т.е. при предположении, что потребители и производители воспринимают рыночные цены, по которым могут купить или продать любое количество благ, в качестве экзогенных (заданных извне) параметров. 2. Простой обмен в двухсубъектной двухпродуктовой экономике Представим экономику, в которой нет производства, состоящую из двух субъектов, A и B, изначально наделенных комбинациями двух благ, X и Y, в количествах ( Индексы соответствуют субъектам A, B, а 0 означает изначальные количества благ, которыми они наделены. Предположим также, что предпочтения субъектов A и B отвечают аксиомам рационального потребителя. Это значит, что для A и B существуют карты безразличия, удовлетворяющие известным условиям: гладкие и непрерывные кривые безразличия, убывающие нормы предельного замещения и т.д. Оба субъекта преследуют цель максимизации индивидуальной полезности. Задача заключается в том, чтобы определить условия, при которых этой цели достигает каждый субъект.
Рисунок 4.1- Изначальный набор благ X и Y у субъекта A
На рисунке 4.1 точка SA представляет изначальное положение (статус-кво) A, наделенного X0A единицами блага X и Y0A единицами блага Y. При отсутствии обмена A должен будет довольствоваться уровнем полезности, соответствующим кривой безразличия U0A, к которой принадлежит точка SA. Если субъекты A и B могут обмениваться благами, у каждого из них появляется возможность увеличить уровень своего удовлетворения (или полезности), перейдя на более высокую кривую безразличия. А эта возможность зависит от норм обмена благами X и Y. Известно, что оптимум потребителя достигается в точке касания его бюджетной прямой и кривой безразличия. Однако наша модель представляет экономику простого обмена, или бартерную экономику, в которой не существует денег. Значит, и нормы обмена благ X и Y не являются их денежными ценами. Кривая предложения Рассмотрение модели начнем с построения кривой предложения, которая имеет здесь специфическое значение, как предложение из запаса. Введем понятие ценности набора благ X и Y. Если принять их цены за P0X и P0Y, то ценность изначального набора составит: M0= P0XX0A+ P0YY0A (4.1) где M0 можно интерпретировать как бюджет субъекта A. Если же цены благ X и Y будут P1X и P1Y, его бюджет составит M1= P1XX0A+ P1YY0A, так что M1 >= M0, или наоборот. Бюджетное уравнение может быть представлено и в виде После подстановки (1) в (2) и упрощения получим
Это значит, что YA=Y0A, если XA=X0A, и что наклон бюджетной прямой – P0X/P0Y. Соответственно при ценах P1X и P1Y уравнение бюджетной прямой имеет вид И вновь изначальный набор субъекта A оказывается принадлежащим бюджетной прямой. Изменился лишь наклон этой прямой, он стал теперь (по абсолютной величине) равен соотношению цен P1X/P1Y вместо P0X/P0Y. Таким образом, бюджетная прямая в любом случае проходит через точку, представляющую изначальное наделение благамиX и Y субъекта A, и что при разном соотношении цен наклон бюджетной прямой окажется разным. Чем «дороже» («дешевле») X относительноY, тем более крут (полог) наклон бюджетной прямой. Наклон бюджетной прямой характеризует соотношение относительных цен, а не их абсолютные значения. Если абсолютные цены обоих благ будут удвоены (или вдвое уменьшены), наклон бюджетной линии не изменится. Две из множества бюджетных прямых показаны на рис. 4.2
Рисунок 4.2 – Бюджетные прямые
Обе они проходят через точку SA, характеризующую изначальное наделение субъекта A благами X и Y. Взаимное расположение линий M0 и M1 отражает то, что соотношение цен P0X/P0Y по абсолютной величине выше соотношения P1X/P1Y. Теперь, когда мы представляем карту безразличия субъекта A, изначально наделенного набором благ (X0A,Y0A), и пучок бюджетных прямых, обеспечивающих неизменную ценность этого набора при разных относительных ценах благ, можем построить его кривую предложения благ к обмену. Обратимся к рис. 4.3, на котором представлено семейство кривых безразличия субъекта A (U0A,…U3A).
Рисунок 4.3 – Семейство кривых безразличия
Изначальное наличие благ представлено точкой SA, лежащей на кривой безразличия U0A. Если относительные цены благ характеризуются бюджетной прямой M0A, которая касается кривой безразличия именно в точке SA, то последняя и будет характеризовать оптимум субъекта A. В этом случае он откажется от обмена со вторым субъектом, поскольку такой обмен ухудшит его положение. Если же относительная цена блага X окажется ниже, так что соотношение цен X и Y будет отображаться бюджетной прямой M1A (вместо M0A), касающейся более высокой кривой безразличия U1A в точке A, наш субъект согласится обменять Y0AY1A единиц блага Y на X0AX1A блага X. Это позволит ему получить большую полезность в точке A, чем в точке SA. Если цена X относительно Y будет и далее снижаться, так, что бюджетная прямая будет поворачиваться вокруг точки SA от M1A до M3A, субъект A сможет достигать все более высоких кривых безразличия, а его оптимум будет смещаться из A в B и затем в C. Множество точек (SA, A, B, C,…) касания кривых безразличия и бюджетных прямых, проходящих через точку SA и имеющих разный наклон, образуют кривую предложения OCA блага Y из его начального запаса Y0A к обмену на благо X. Важно отметить, что в двухпродуктовой экономике кривая предложения блага Y, есть в то же время и кривая спроса субъекта A на благо X. Это прямо свидетельствует из того, что она представляет множество оптимальных для субъекта A наборов благ X и Y при снижении цены товара X относительно Y. 3. Коробка Эджуорта и контрактная линия
Коробка Эджуорта представляет совмещенные карты безразличия двух субъектов, A и B, причем карта безразличия B повернута на 180°, так что начала координат каждой из двух карт безразличия становятся противолежащими вершинами прямоугольника – коробки (A, B). Вместе с координатными осями карты безразличия B на 180° поворачивается и все семейство его кривых безразличия, так что кривые безразличия субъекта B выпуклы вправо вверх, тогда как кривые безразличия A остаются выпуклыми, как обычно, влево вниз.
Рисунок 4.4 – Коробка Эджуорта
На нижней горизонтальной оси AXA, откладывается количество блага X, которым располагает A, на верхней оси BXB, - количество того же блага X, которым располагает B. Аналогично на левой вертикальной оси, AYA, откладывается количество блага Y, которым располагает A, а на правой оси, BYB, - количество блага Y, которым располагает B. Границы коробки Эджуорта соответствуют фиксированным количествам благ X и Y, находящимся в распоряжении субъектов A и B, так что AL=BK=XA+XB и AK=BL=YA+YB. (4.5) Количества благ X и Y фиксированы, потому что в рассматриваемой нами экономике нет производства. Любая точка в пределах коробки Эджуорта характеризует некоторое распределение двух благ X и Y между двумя субъектами A и B. Пусть точка S0 будет точкой изначального распределения благ между субъектами. Тогда субъект A получит набор S0A(X0A, Y0A), а субъект B – набор S0B(X0B,Y0B). При этом все наличное количество благ X и Y будет без остатка распределено между ними, так что AX0A+BX0B=AL=BK (4.6) AY0A+BY0B=AK=BL. (4.7) Заметим, что изначальное распределение благ S0 субъекты A и B сочтут неудовлетворительным, ведь в точке S0 наклоны пересекающихся здесь кривых безразличия A и B (U0A и U0B) неодинаковы, что означает и неравенство в этой точке предельных норм замены благ X и Y. У обоих субъектов возникнет желание улучшить свое положение посредством взаимного обмена некоторыми количествами благ X и Y. Это желание улучшить свое положение посредством обмена исчезнет тогда, когда такое улучшение станет невозможным. Склонность к обмену исчезнет только тогда, когда конечное, достигнутое в ходе обмена распределение благ X и Y между субъектами окажется таким, что точка, отображающая его в коробке Эджуорта, будет точкой касания кривых безразличия обоих субъектов. Поскольку карта безразличия каждого субъекта содержит бесконечное множество его кривых безразличия, коробка Эджуорта будет вмещать и бесконечное множество точек касания кривых безразличия двух субъектов. Это множество образует так называемую контрактную линию AB. Она представляет все множество взаимоприемлемых результатов обмена двух субъектов. Однако не все обмены будут одинаково выгодны обоим. При изначальном распределении S0 ни одна точка на контрактной линии AB, лежащая ниже и левее F или выше и правее G, не может характеризовать результатов добровольного и взаимоприемлемого обмена благами X и Y между субъектами A и B. Все точки контрактной линии ниже и левее F принадлежат кривым безразличия A, более низким, чем U0A, а все ее точки, расположенные выше и правее G, принадлежат кривым безразличия B, более низким, чем U0B. Таким образом, взаимоприемлемый обмен возможен в интервале FG контрактной кривой AB. При обмене каждый субъект движется вдоль своей кривой предложения, максимизируя свою функцию полезности при меняющихся относительных ценах благ. Максимальное удовлетворение (полезность) для обоих субъектов возможно лишь в том случае, когда конечное распределение благ соответствует точке пересечения обеих кривых предложения в коробке Эджуорта. Каждая точка максимума благосостояния есть распределение, эффективное по Парето, и каждое распределение, эффективное по Парето, есть точка максимума благосостояния. Выводы: 1. Если в точке, характеризующей в коробке Эджуорта изначальное распределение двух благ, кривые безразличия двух индивидов пересекаются (а не касаются одна другой), обмен благами может способствовать достижению каждым субъектом более высокого уровня удовлетворения (полезности). 2. Конечное распределение двух благ между двумя индивидами соответствует точке пересечения их кривых предложения, которая в то же время является и точкой касания их кривых безразличия и лежит на контрактной прямой. 3. В этой точке достигнутого в процессе обмена равновесия предельные нормы замены двух благ для обоих субъектов одинаковы и равны соотношению цен:
или
Контрольные вопросы 1. Распределение ресурсов эффективное по Парето. 2. Эффективность потребления, эффективность производства и эффективность производимого набора товаров. 3. Эффективность, единственность и устойчивость общего равновесия. 4. Что демонстрирует коробка Эджуорта? 5. Что представляет собой контрактная линия?
Задачи к теме 4 Задача 1 Пусть экономика состоит из двух индивидов, потребляющих два блага (X и Y). Функции полезности индивидов 1 и 2 1. Если изначальное размещение благ X1 = 2, Y1 = 2; X2 = 8, Y2 = 8, то каковы полезности индивидов 1 и 2? Постройте коробку Эджуорта, контрактную кривую и отметьте точку изначального размещения. 2. «Секретарь рынка» решил, что полезность индивида 1 (U1) должна равняться 5 единицам, и полезность индивида 2 – 5 единицам. Покажите в коробке Эджуорта возможные варианты перераспределения благ, которые при неизменных равновесных ценах обеспечат желаемое «секретарем рынка» распределение полезностей. Задача 2 Пусть в экономике имеется 1 000 единиц блага X и 1 000 единиц блага Y, а также два индивида (индивид 1 и индивид 2), потребляющих эти блага. Изначально индивид 1 обладает 300 единиц X и 700 единиц Y, а индивид 2 – 700 единиц X и 300 единиц Y. Функции полезности индивидов соответственно
1. Нарисуйте коробку Эджуорта, соответствующую этой экономике. 2. Каковы уравнения кривых безразличия, проходящих через точку изначального размещения благ между индивидами? Изобразите их в коробке Эджуорта. Вы можете воспользоваться следующими таблицами точек, предварительно заполнив их:
3. Заштрихуйте область, представляющую Парето-улучшение по отношению к изначальному размещению благ между индивидами. 4. Каково уравнение контрактной кривой в данной экономике? Изобразите ее в коробке Эджуорта. 5. Предположим, что некий «секретарь рынка» объявил цены благ. Цена X PX = 1 ден. ед. и цена Y PY = 2 ден. ед. Более того, он изъял блага у каждого индивида и заменил их деньгами в соответствии со стоимостью. Затем «секретарь рынка» предложил каждому заказать у него желаемое количество благ (такое количество, которое максимизирует его полезность при данном бюджетном ограничении). Какое количество благ X и Y закажут индивиды 1 и 2? Будет ли заказанная комбинация благ эффективной? Сможет ли «секретарь рынка» удовлетворить их заявки? 6. «Секретарь рынка» поднял цену блага X PX = 2 ден. ед., соблюдая все прежние условия. Сможет ли он удовлетворить заявки? Будет ли полученное размещение благ эффективным? 7. Постройте в коробке Эджуорта кривые безразличия, проходящие через решение пункта 6. Вы можете воспользоваться следующими таблицами точек, предварительно заполнив их:
Постройте в коробке Эджуорта бюджетную линию пункта 6.
Задача 3 Пусть экономика состоит из двух индивидов, потребляющих два блага (X и Y). Функции полезности индивидов 1 и 2 1. Если изначальное размещение благ X1 = 2, Y1 = 2; X2 = 8, Y2 = 8, то каковы полезности индивидов 1 и 2? Постройте коробку Эджуорта, контрактную кривую и отметьте точку изначального размещения. 2. «Секретарь рынка» решил, что полезность индивида 1 (U1) должна равняться 5 единицам, и полезность индивида 2 – 5 единицам. Покажите в коробке Эджуорта возможные варианты перераспределения благ, которые при неизменных равновесных ценах обеспечат желаемое «секретарем рынка» распределение полезностей. Задача 4 Пусть имеется экономика с двумя индивидами А и В. Их предпочтения представлены функциями полезности: Рассчитайте равновесные цены (относительные) и равновесное размещение благ между индивидами.
Задача 5 Функция полезности индивида А: Индивид А изначально располагает 10 единицами блага Y и ни одной единицей блага X. Индивид В изначально располагает 20 единицами блага X и 5 единицами блага Y. Рассчитайте равновесные цены (относительные) и равновесное размещение благ между индивидами.
Задача 6 Рассмотрим экономику обмена с двумя индивидами, чьи функции полезности заданы как Рассчитайте равновесные цены (относительные) и равновесное размещение благ между индивидами Задача 7 Изобразите графически коробку Эджуорта, контрактную линию, произвольную точку оптимального размещения благ между потребителями, кривые безразличия, проходящие через эту точку, бюджетную линию. Опишите экономический смысл элементов графика.
Тест по теме 4
1. Равновесные модели в микроэкономике используются: а) для изучения поведения отдельных экономических субъектов; б) для изучения взаимодействия экономических субъектов; в) для изучения макроэкономической динамики; г) нет верного ответа.
2. Если на каждом из рынков выполняются условия совершенной конкуренции, то: а) общее экономическое равновесие невозможно; б) общее экономическое равновесие будет наблюдаться при любых условиях; в) общее экономическое равновесие может существовать при определенной системе цен; г) общее экономическое равновесие может существовать, если экономические субъекты ведут себя как ценоискатели.
3. Если абсолютные цены в двухпродуктовой экономике обмена вырастут в n раз, то: а) угол наклона бюджетной линии увеличится; б) угол наклона бюджетной линии уменьшится; в) угол наклона бюджетной линии не изменится; г) бюджетная линия сдвинется параллельно.
4. На диаграмме Эджуорта (рис. 4.1) представлена контрактная кривая. Начальный запас индивидов А и В характеризуется точкой S0. Можно утверждать, что в этой ситуации: а) только индивид А желает принять участие в обмене; б) только индивид В желает принять участие в обмене; в) индивиды А и В находятся в равновесии и не желают обмениваться благами; г) и индивид А, и индивид В желают принять участие в обмене благами.
рис. 4.1. Коробка Эджуорта
5. На диаграмме Эджуорта (рис. 4.1) представлена контрактная кривая. Начальный запас индивидов А и В характеризуется точкой S0. Общее равновесие может быть достигнуто: а) в любой точке на контрактной линии; б) в любой точке на контрактной линии на интервале CD; в) либо в точке С, либо в точке D; г) только в точке E.
6. На диаграмме Эджуорта (рис. 4.1) представлена контрактная кривая. Начальный запас индивидов А и В характеризуется точкой S0. Точкой, представляющей Парето-улучшение распределения благ между индивидами по сравнению с первоначальным распределением является: а) точка F; б) точки C, D и Е; в) точка E; г) все ответы верны.
7. На диаграмме Эджуорта (рис. 4.1) представлена контрактная кривая. Начальный запас индивидов А и В характеризуется точкой S0. Наиболее выгодное для индивида В равновесное распределение благ представлено точкой: а) D; б) Е; в) С; г) F.
8. В коробке Эджуорта контрактная линия – это: а) множество точек касания кривых безразличия индивидов А и В; б) множество возможных положений общего экономического равновесия в зависимости от первоначального распределения благ между индивидами; в) множество эффективных по Парето распределений благ между индивидами; г) все ответы верны.
9. Если за счет перераспределения благ между индивидами А выигрывает больше, чем теряет В, можно утверждать, что: а) исходное распределение благ было неэффективным по Парето; б) итоговое распределение благ представляет собой Парето-улучшение по сравнению с исходным состоянием; в) итоговое распределение эффективно по Парето; г) нет верного ответа.
10. Субъекты в двухпродуктовой экономике обмена вступают в обмен с целью: а) победить в конкурентной борьбе друг с другом; б) достичь более справедливого распределения благ; в) повысить уровень своего удовлетворения (полезности); г) все ответы верны.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.75 (0.01 с.) |

 ) и соответственно (
) и соответственно ( ).
).
 (4.2)
(4.2) . (4.3)
. (4.3)
 . (4.4)
. (4.4)


 , (4.8)
, (4.8) . (4.9)
. (4.9) и
и  соответственно. Экономика располагает 10 единицами блага X и 10 единицами блага Y.
соответственно. Экономика располагает 10 единицами блага X и 10 единицами блага Y. и
и  .
. и
и  . Индивид А изначально располагает 2 единицами блага X и ни одной единицей блага Y. Индивид В изначально располагает 3 единицами блага Y и ни одной единицей блага X.
. Индивид А изначально располагает 2 единицами блага X и ни одной единицей блага Y. Индивид В изначально располагает 3 единицами блага Y и ни одной единицей блага X. . Функция полезности индивида В:
. Функция полезности индивида В: 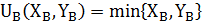 .
. и
и  , где
, где  . В изначальном наделении индивид 1 располагает единицей блага Y, а индивид 2 – единицей блага X.
. В изначальном наделении индивид 1 располагает единицей блага Y, а индивид 2 – единицей блага X.


