
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гармонические функции. Для простоты изложения ограничимся трехмерным евклидовым пространством В плоском случае Выделим ограниченную связную область Опр1. Функция
Рассмотрим аналитическую функцию Получим частные решения уравнения (2):
Умножив
которое называется фундаментальным решением уравнения Лапласа на плоскости Заметим, что функция (3) удовлетворяет уравнению (2) во всех точках плоскости за исключением точки В случае трехмерного пространства где Для проверки вычислим производные
После подстановки в уравнение (1) получим тождество. Заметим, что функция (4) удовлетворяет уравнению (1) во всех точках пространства
1. Предмет дифференциальных уравнений с частными производными. Историческое развитие исследований уравнений с частными производными, их использование в методах математического моделирования реальности. Современное состояние науки. 2. Основные понятия об уравнениях с частными производными. Классические решения простейших уравнений с частными производными. Общее решение гиперболических уравнений второго порядка с двумя переменными. 3. Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными. 4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик. 5. Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными. 6. Классификация уравнений второго порядка со многими независимыми переменными. 7. Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами. Исключение младших производных в уравнениях. 8. Постановка задачи Коши. Теорема Коши-Ковалевской. 9. Метод характеристик. Формула Даламбера для решения задачи Коши для уравнения колебаний струны. 10. Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши. 11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений. 12. Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности. 13. Пространство основных функций. Обобщенные функции и их свойства. 14. Сингулярные обобщенные функции, дельта-функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными. 15. Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова. 16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация. 17. Задача Шт - Л для ОДУ второго порядка. Свойства собственных функций и собственных значений задачи Ш - Л. 18. Метод разделения переменных при решении смешанных задач для уравнения колебаний струны. Решение первой смешанной задачи, обоснование решения. 19. Постановка смешанных задач для уравнения теплопроводности, физическая интерпретация. 20. Решение смешанных задач для уравнения теплопроводности методом разделения переменных. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи. 21. Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа. 22. Формулы Грина для оператора Лапласа. Интегральная формула Грина для гармонических функций. 23. Свойства гармонических функций. Принцип максимума и минимума для гармонических функций, следствия. 24. Краевые задачи Дирихле, Неймана и третьего рода для эллиптических уравнений. Спектральная задача для оператора Лапласа. Корректность внутренних и внешних краевых задач для уравнения Лапласа и Пуассона. 25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона. 26. Динамические модели денежных накоплений семьи с использованием стохастических дифференциальных уравнений. 27. Одномерные марковские стохастические процессы в моделировании случайных денежных накоплений. Условная плотность вероятностей стохастического процесса и ее свойства. 28. Параболические уравнения Колмогорова. Вывод параболического уравнения денежных накоплений ансамбля семей. 29. Постановка задач для уравнения денежных накоплений, смешанные задачи с нелокальными граничными условиями. 30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито. 31. Связь задачи Коши для стохастического уравнения с задачей Коши для уравнения Колмогорова. 32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито. 33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений. 34. Уравнение для плотности распределения акций в пространстве цен и смешанная задача для него. 35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.68 (0.006 с.) |

 с декартовой системой координат
с декартовой системой координат  . В пространстве
. В пространстве 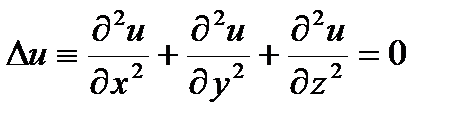 . (1)
. (1) имеем уравнение
имеем уравнение  .(2):
.(2): . Пусть граница
. Пусть граница  области
области  представляет собой поверхность без самопересечений,
представляет собой поверхность без самопересечений,  .
. называется гармонической в области
называется гармонической в области  , если
, если  и удовлетворяет уравнению Лапласа (4.1) в области
и удовлетворяет уравнению Лапласа (4.1) в области  ,
,  . Запишем комплексное число
. Запишем комплексное число  в виде
в виде  , где
, где 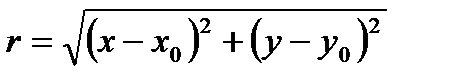 ,
,  , тогда
, тогда 
 .
. ,
,  .
.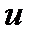 на числовой множитель
на числовой множитель  , получим решение
, получим решение , (3)
, (3) .
.
 для уравнения Лапласа
для уравнения Лапласа  (1) решение вида
(1) решение вида  , (4)
, (4) - координаты фиксированной точки
- координаты фиксированной точки  , называется фундаментальным решением уравнения Лапласа в
, называется фундаментальным решением уравнения Лапласа в  .
. ,
,  ,
, , где
, где 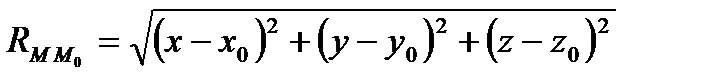 .
. .
.


