
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация уравнений второго порядка со многими независимыми переменными.Содержание книги
Поиск на нашем сайте
Рассм. линейные ур-ния 2-го порядка n независимых переменных:
Опр. Выражение По главной части ур-ния(19) построим полином P(t;x): P(t;x) = Опр. Поверхность Г заданная ур-нием(22) наз-ся характеристической поверхностью ур-ния(19), если во всех точках поверхности Г ф-ция Опр. Ур-ние(19) Опр. Ур-ние (19) наз-ся ур-нием гиперболического типа в т. Опр. Ур-ние (19) в т. Опр. Ур-ние (19) в т. Опр. Ур-ние (19) Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши. Учитывая общую постановку з.Коши, сформулируем з.Коши для ур-ия второго порядка с двумя независимыми переменными, т.е в пр-ве R2: L(u)
где D-плоская область в R2; Г-линия внутри области D, Г Для строгой матем.постановки задачи Коши необходимо ввести след.прост-ва ф-ий: V1(Г)-прос-ва начальных ф-ий Опр. З.Коши поставлена корректно в прос-вах V1, V2, V, если выполнены три условия корректности: 1)для любых нач.ф-ий Если не выполнено хотя бы одно из условий корректности, то задача называется некорректно поставленной. Если же не выполнено третье условие корректности, то задача Коши наз-ся неустойчивой по нач.данным. Процедура построения решения задачи Коши для ур.колебания струны показывает, что любое классическое решение з.Коши для ур.колебания струны представимо формулой Даламбера Пример Адамара. На плоскости R2 рассмотрим эллиптическое ур-ие Лапласа, для которого поставим з.Коши с нач.усл. на линии Г(у=0):
где n-фиксированный положит.параметр. Решения данных задач определяются выражениями u1=0, u2=
Очевидно, что нер-во (6) не выполнено при дост. Больших значениях пар-ра n, т.к. 11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений. Рассм. з.Коши для однор. параб. ур-ия с пост.коэф.:
F[ F[
G(x,y,t)= Непосредственно вычисляя интеграл, получим: = u(t,x)= ф-ия G, введенная по правилу(3) наз-ся фундамент. решением ур-ия (1). С помощью него, решение з.Коши записывается в виде(4). Аналогично происходит применение интегральных преобразований к другим задачам мат.физики.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (19), где x= (
(19), где x= ( ) точка обл-ти Ω
) точка обл-ти Ω  ,
,  =
=  (коэф. симметричны).
(коэф. симметричны). наз-ся главной частью ур-ния (19).
наз-ся главной частью ур-ния (19). (21). Полином (21) наз-ся характерестическим полиномом ур-ния с частными производ. (19)(УЧП). Он представляет собой квадратичную форму с переменными коэф. Зафиксируем некот. точку
(21). Полином (21) наз-ся характерестическим полиномом ур-ния с частными производ. (19)(УЧП). Он представляет собой квадратичную форму с переменными коэф. Зафиксируем некот. точку  тогда многочлен P(t;
тогда многочлен P(t;  ) представляет собой квадратичную форму с постоянными коэф. Рассм. некоторую поверхность Г<Ω кот. задаётся ур-нием:
) представляет собой квадратичную форму с постоянными коэф. Рассм. некоторую поверхность Г<Ω кот. задаётся ур-нием:  где
где  - дважды непрерывно-диф. на обл-ти
- дважды непрерывно-диф. на обл-ти  (
( ).
). (23). Ур-ние (23) наз-ся ур-нием характеристик дляУЧП (19). Классификацию ур-ния (19) в т.
(23). Ур-ние (23) наз-ся ур-нием характеристик дляУЧП (19). Классификацию ур-ния (19) в т.  к эллиптическому типу в т.
к эллиптическому типу в т.  если в этой точке квадратич. форма(21) P(t;
если в этой точке квадратич. форма(21) P(t;  ) знакоопределённая, т.е при приведении её к сумме квадратов все коэф.равны либо 1, либо -1.
) знакоопределённая, т.е при приведении её к сумме квадратов все коэф.равны либо 1, либо -1. после приведения квадратичной формы P(t;
после приведения квадратичной формы P(t;  +b
+b  в D, (1)
в D, (1) (2)
(2) С2;
С2; 
 ; V(D)-прос-во ф-ий u, в котором отыскивается решение задачи Коши. Для классических решений V(D)
; V(D)-прос-во ф-ий u, в котором отыскивается решение задачи Коши. Для классических решений V(D)  C2(D).
C2(D). сущ.решение задачи u
сущ.решение задачи u  ; 2) для любых нач.ф-ий
; 2) для любых нач.ф-ий  (
( +
+  . Отсюда следует существование и единственность решения задачи в прос-ве V.
. Отсюда следует существование и единственность решения задачи в прос-ве V. в области D=
в области D=  , (3)
, (3) (4). Ур-ие (3) явл-ся ур-ем типа Ковалевской, поэтому в случае аналитических ф-ий
(4). Ур-ие (3) явл-ся ур-ем типа Ковалевской, поэтому в случае аналитических ф-ий  на основании теоремы Ковалевской заключаем, что задача (3),(4) имеет единтств. аналитическое решение в некоторой достаточно малой окрестности линии Г. Т.о, первые два условия корректности выполнены. Исследуем третье условие корректности, т.е условие о непрерывной зависимости от начальных ф-ий. Для этого рассмотрим две задачи Коши с различными нач.усл. специального вида:
на основании теоремы Ковалевской заключаем, что задача (3),(4) имеет единтств. аналитическое решение в некоторой достаточно малой окрестности линии Г. Т.о, первые два условия корректности выполнены. Исследуем третье условие корректности, т.е условие о непрерывной зависимости от начальных ф-ий. Для этого рассмотрим две задачи Коши с различными нач.усл. специального вида:

 ,
,  (5)
(5)

 Введем прост-ва ф-ий V1=V2=C0A(R1), V= C0A(D), где C0A- прос-во ограниченных аналитических ф-ий.
Введем прост-ва ф-ий V1=V2=C0A(R1), V= C0A(D), где C0A- прос-во ограниченных аналитических ф-ий. (u1,u2)=
(u1,u2)= 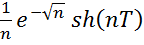 <
<  (6)
(6) Т.о., з.Коши для эллиптического ур-ия (3), (4) поставлена некорректно, т.к. не выполнено третье условие корректности из определения.
Т.о., з.Коши для эллиптического ур-ия (3), (4) поставлена некорректно, т.к. не выполнено третье условие корректности из определения. +
+  (1)
(1) (2). с нач.усл.(2), где ф-ия
(2). с нач.усл.(2), где ф-ия  -ограничена и непрерывна на
-ограничена и непрерывна на  . Решим з.Коши методом интегральных преобр.. Применим преобр. Фурье по аргументу х: U(t)=F[u]. Формально изображение U зависит не только от аргумента t, но и переменной
. Решим з.Коши методом интегральных преобр.. Применим преобр. Фурье по аргументу х: U(t)=F[u]. Формально изображение U зависит не только от аргумента t, но и переменной  . Однако эту переменную будем считать пар-ром и не вкл.ее в число аргументов ф-ии U. Используя св-ва преобр. Фурье:
. Однако эту переменную будем считать пар-ром и не вкл.ее в число аргументов ф-ии U. Используя св-ва преобр. Фурье: ]=
]= 
 ]=
]= 
 -образ ф-ии
-образ ф-ии  =(
=( )U, U(0)=
)U, U(0)=  . Получим з.Коши для обыкн. ДУ с разделяющимися перем. U(t)=
. Получим з.Коши для обыкн. ДУ с разделяющимися перем. U(t)=  -решение ДУ. Возвращаясь к з.Коши (1),(2) получим: u(t,x)=
-решение ДУ. Возвращаясь к з.Коши (1),(2) получим: u(t,x)= 
 (3)
(3)
 (4)
(4)


