
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параболические уравнения КолмогороваСодержание книги
Поиск на нашем сайте
Одномерные уравнения Колмогорова. Рассмотрим марковский стохастический процесс c переходной функцией плотности вероятностей Теорема 5.1. Пусть: 1) для переходной функции плотности вероятностей 2) плотность 3) функции 4) производные Тогда плотность
Постановка задач для уравнения денежных накоплений ансамбля семей. Как было ранее показано, если динамика денежных накоплений отдельной семьи подчиняется стохастическому уравнению (6.13), где
7.Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами. Исключение младших производных в уравнениях. Уравнение характеристик. Рассмотрим класс линейных уравнений второго порядка с где коэффициенты Опр. Поверхность
Уравнение (7) называется уравнением характеристик Приведение к каноническому виду уравнений с постоянными коэффициентами. Рассмотрим уравнение (1) с постоянными коэффициентами
Приведем его к каноническому виду с помощью замены независимых переменных. Для этого в уравнении (8) перейдем от переменных Вычислим производные
После подстановки в (8) получим уравнение в новых переменных:
где
8. Постановка задачи Коши. Теорема Коши-Ковалевской. Рассмотрим
с достаточно гладкими коэффициентами. Тип уравнения (1) может быть любым. В пространстве На поверхности
Условия (3) называются начальными условиями. Задача Коши 1(классическая постановка)
Теорема Ковалевской. Если коэффициенты уравнения (*)
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.007 с.) |

 . Выведем два уравнения с частными производными, которым удовлетворяет переходная функция по двум парам переменных, соответственно по
. Выведем два уравнения с частными производными, которым удовлетворяет переходная функция по двум парам переменных, соответственно по 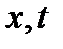 и по
и по  . Вывод уравнений оформим в виде двух теорем.
. Вывод уравнений оформим в виде двух теорем. выполнены свойства А;
выполнены свойства А; при фиксированных
при фиксированных  и
и 
 ограничена, то есть
ограничена, то есть  , где
, где  не зависит от
не зависит от  и
и  ;
;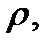


 , непрерывны, как функции двух переменных
, непрерывны, как функции двух переменных  и
и  на множестве
на множестве 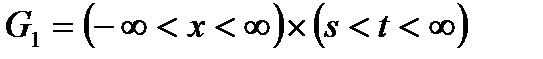 ;
; 


 .
. удовлетворяет параболическому уравнению с частными производными по переменным
удовлетворяет параболическому уравнению с частными производными по переменным  :
: 
 .
. - марковский стохастический процесс с переходной функцией пло-тности вероятностей
- марковский стохастический процесс с переходной функцией пло-тности вероятностей  (5.10), тогда плотность
(5.10), тогда плотность 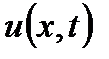 ансамбля семей в пространстве накоплений N
ансамбля семей в пространстве накоплений N  удовлетворяет параболическому уравнению (6.30):
удовлетворяет параболическому уравнению (6.30):  , (6.56),где
, (6.56),где 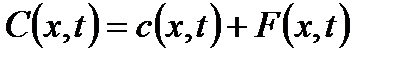 . Из множества решений уравнения (6.56) необходимо найти единственное решение, которое адекватно описывает динамику накоплений выделенного множества семей, схожих по своей экономической деятельности. Для выделения единственного решения на искомую функцию
. Из множества решений уравнения (6.56) необходимо найти единственное решение, которое адекватно описывает динамику накоплений выделенного множества семей, схожих по своей экономической деятельности. Для выделения единственного решения на искомую функцию  необходимо наложить некоторые дополнительные условия, возникающие в зависимости от дополнительной информации, которой обладает исследователь. Сформулируем краевые задачи для уравнения (6.56) по аналогии с краевыми задачами математической физики.
необходимо наложить некоторые дополнительные условия, возникающие в зависимости от дополнительной информации, которой обладает исследователь. Сформулируем краевые задачи для уравнения (6.56) по аналогии с краевыми задачами математической физики. независимыми переменными:
независимыми переменными:  , (1)
, (1) определены в области
определены в области  .Выделим главную часть уравнения
.Выделим главную часть уравнения  . (2) Рассмотрим
. (2) Рассмотрим  и поставим в соответствие производным функции
и поставим в соответствие производным функции  числовые выражения по следующему правилу
числовые выражения по следующему правилу  ,(3) тогда главной части (3) соответствует полином по переменным
,(3) тогда главной части (3) соответствует полином по переменным 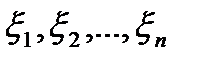 :
:  . (4) Полином (4) по переменным
. (4) Полином (4) по переменным  называется характеристическим полиномом. Зафиксируем точку
называется характеристическим полиномом. Зафиксируем точку  , получим квадратичную форму с постоянными коэффициентами
, получим квадратичную форму с постоянными коэффициентами  . (5) Рассмотрим поверхность
. (5) Рассмотрим поверхность  , принадлежащую области
, принадлежащую области  , которую зададим уравнением
, которую зададим уравнением  ,(6), где
,(6), где  .
. удовлетворяет ур.
удовлетворяет ур.
 (8)
(8) к новым переменным
к новым переменным  , производя замену
, производя замену  , (9) Причем преобразование (9) не вырожденное det(
, (9) Причем преобразование (9) не вырожденное det( )
) 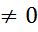
 ,
, .
.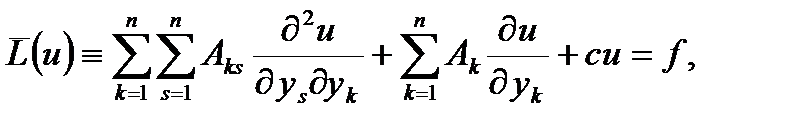
 , тогда уравнение (8) с помощью преобразования (9) приводится к каноническому виду
, тогда уравнение (8) с помощью преобразования (9) приводится к каноническому виду  .
. . Пусть
. Пусть  - связная область в пространстве
- связная область в пространстве  , точка
, точка  . В области
. В области  зададим уравнение с частными производными второго порядка
зададим уравнение с частными производными второго порядка (1)
(1) зададим незамкнутую без самопересечений поверхность
зададим незамкнутую без самопересечений поверхность  с помощью уравнения
с помощью уравнения  (2) где функция
(2) где функция  является дважды непрерывно дифференцируемой функцией, то есть
является дважды непрерывно дифференцируемой функцией, то есть  , а
, а 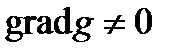 в любой точке
в любой точке  .
. 
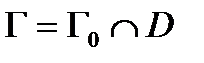 часть поверхности, лежащей внутри области
часть поверхности, лежащей внутри области  . Будем предполагать, что область
. Будем предполагать, что область  представима в виде
представима в виде  , где
, где  0
0  ,
, 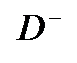 не имеют общих точек с поверхностью
не имеют общих точек с поверхностью  :
:  ,
, 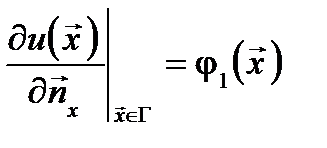 , (3) где
, (3) где  ,
, 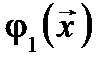 - заданные функции на поверхности
- заданные функции на поверхности  - единичная нормаль к поверхности
- единичная нормаль к поверхности  ;
;  - производная по направлению нормали
- производная по направлению нормали  , которая определяется выражением
, которая определяется выражением ,
,  . (4)
. (4) в области
в области  ,
,  . (6)
. (6) , которая удовлетворяет уравнению (5) в области
, которая удовлетворяет уравнению (5) в области  , которая удовлетворяет указанным требованиям, называется классическим решением задачи Коши.
, которая удовлетворяет указанным требованиям, называется классическим решением задачи Коши. и нач. фу-ии (**)
и нач. фу-ии (**) 
 , являются аналитическими функциями, тогда для любой точки y0 кривой Г(t-0) существует окрестность этой точки, целиком лежащей в обл.
, являются аналитическими функциями, тогда для любой точки y0 кривой Г(t-0) существует окрестность этой точки, целиком лежащей в обл.  в кот. реш. з.Коши (*), (**) единственной в пространстве аналитических функций.
в кот. реш. з.Коши (*), (**) единственной в пространстве аналитических функций.


