
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.Стр 1 из 9Следующая ⇒
Предмет дифференциальных уравнений с частными производными. Историческое развитие исследований уравнений с частными производными, их использование в методах математического моделирования реальности. Современное состояние науки. При математ. моделировании различных явлений получ-ся ДУ, в кот. входит неизвестная ф-ция, зависящая от многих независимых переменных и, следоват., ур-ние, поскольку оно явл-ся ДУ, содержит частные производные от неизвестной ф-ции. Т.к. почти все физич. явления описыв-ся ДУвЧП, то часто в тех случаях, когда ДУ описывает физич. процесс, эти ур-ния наз-ся ур-ниями мат. физики. Однако надо иметь в виду, что ДУвЧП опис-ся не только физич., но и химич.,биологич. и экономич. процессы и явления. Типичный пример – ур-ние теплопроводности. Большой вклад в развитие ДУвЧП внесли многие математики мира. Для решения задач ДУвЧП были созданы новые разделы: функциональный анализ, теория обобщенных ф-ций, теория новых функциональных простр-в. Отметим самые известные имена в истории развития ДУвЧП. И.Г.Петровский положил начало развития общей теории линейных систем в частных производных, а также их классификацию. С.Л.Соболев ввел новое понятие – обобщенное решение дифф. ур-ния; им были введены и изучены новые функциональные пространства. Исследования в области ДУвЧП идут в двух направлениях. С одной стороны: создается общая теория ДУвЧП, т.е. для общих ур-ний и граничных условий изучаются вопрося существования решений, их единственность и устойчивость. С другой стороны: существует много ДУвЧП, описывающих те или иные физические или биологические явления, решения которых нужно изучить при различных граничных условиях, в том числе изучить качественные свойства этих решений.
2.Основные понятия об уравнениях с частными производными. Классические решения простейших уравнений с частными производными. Общее решение гиперболических уравнений второго порядка с двумя переменными. Рассмотр. n-мерное евклидово простр-во Опр. Множ-во ф-ций
Рассмотр произв ф-цию F(x1,..,xn,z1,…,zn) Опр. Диффер ур-нием с частн производн относит ф-ции u=u(x) будем назыв рав-во: F(x,u, C помощью ф-ции F введем диффер оператор L он действует на ф-цию u: L[u]= F(x,u, Опр. Классическим решением ур-ния(1)на обл Ω назыв такую ф-цию u Из записи (1) Ур-ние (1) иногда можно записать в виде: L[u]=f(x).Такое ур-ние назывюлинейным ур-нием с частнами производнами, если для оператора L выполнены условия линейности: L[αu]=αL[u], α L[u1+u2]=L[u1]+L[u2] (3) Утвержд. Любое линейн ур-ние с частн производн порядка m имеет вид:
Т.е.L[u]= Если в ур-нии (4) ф-ция f(x)=0, то такое ур-ние наз-ся однородным, в противн случ неоднородным.
Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши. Учитывая общую постановку з.Коши, сформулируем з.Коши для ур-ия второго порядка с двумя независимыми переменными, т.е в пр-ве R2: L(u)
где D-плоская область в R2; Г-линия внутри области D, Г Для строгой матем.постановки задачи Коши необходимо ввести след.прост-ва ф-ий: V1(Г)-прос-ва начальных ф-ий Опр. З.Коши поставлена корректно в прос-вах V1, V2, V, если выполнены три условия корректности: 1)для любых нач.ф-ий Если не выполнено хотя бы одно из условий корректности, то задача называется некорректно поставленной. Если же не выполнено третье условие корректности, то задача Коши наз-ся неустойчивой по нач.данным.
Процедура построения решения задачи Коши для ур.колебания струны показывает, что любое классическое решение з.Коши для ур.колебания струны представимо формулой Даламбера Пример Адамара. На плоскости R2 рассмотрим эллиптическое ур-ие Лапласа, для которого поставим з.Коши с нач.усл. на линии Г(у=0):
где n-фиксированный положит.параметр. Решения данных задач определяются выражениями u1=0, u2=
Очевидно, что нер-во (6) не выполнено при дост. Больших значениях пар-ра n, т.к. 11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений. Рассм. з.Коши для однор. параб. ур-ия с пост.коэф.:
F[ F[
G(x,y,t)= Непосредственно вычисляя интеграл, получим: = u(t,x)= ф-ия G, введенная по правилу(3) наз-ся фундамент. решением ур-ия (1). С помощью него, решение з.Коши записывается в виде(4). Аналогично происходит применение интегральных преобразований к другим задачам мат.физики.
Первая смешанная задача.
При заданных функциях Третья смешанная задача.
Первая смешанная задача.
При заданных функциях Условия согласования: Задача (2)-(4) описывает процесс распространения тепла в тонком стержне длины
Вторая смешанная задача.
При заданных функциях Условия согласования: Граничные условия (7) означают, что в торцах стержня Третья смешанная задача.
При заданных функциях Условия согласования: Граничные условия (10) моделируют теплообмен стержня через торцы Заметим, что для существования классических решений сформулированных задач необходимо на начальные и граничные функции и на правую часть уравнения теплопроводности накладывать некоторые дополнительные условия. Предмет дифференциальных уравнений с частными производными. Историческое развитие исследований уравнений с частными производными, их использование в методах математического моделирования реальности. Современное состояние науки. При математ. моделировании различных явлений получ-ся ДУ, в кот. входит неизвестная ф-ция, зависящая от многих независимых переменных и, следоват., ур-ние, поскольку оно явл-ся ДУ, содержит частные производные от неизвестной ф-ции. Т.к. почти все физич. явления описыв-ся ДУвЧП, то часто в тех случаях, когда ДУ описывает физич. процесс, эти ур-ния наз-ся ур-ниями мат. физики. Однако надо иметь в виду, что ДУвЧП опис-ся не только физич., но и химич.,биологич. и экономич. процессы и явления. Типичный пример – ур-ние теплопроводности. Большой вклад в развитие ДУвЧП внесли многие математики мира. Для решения задач ДУвЧП были созданы новые разделы: функциональный анализ, теория обобщенных ф-ций, теория новых функциональных простр-в. Отметим самые известные имена в истории развития ДУвЧП. И.Г.Петровский положил начало развития общей теории линейных систем в частных производных, а также их классификацию. С.Л.Соболев ввел новое понятие – обобщенное решение дифф. ур-ния; им были введены и изучены новые функциональные пространства. Исследования в области ДУвЧП идут в двух направлениях. С одной стороны: создается общая теория ДУвЧП, т.е. для общих ур-ний и граничных условий изучаются вопрося существования решений, их единственность и устойчивость. С другой стороны: существует много ДУвЧП, описывающих те или иные физические или биологические явления, решения которых нужно изучить при различных граничных условиях, в том числе изучить качественные свойства этих решений.
2.Основные понятия об уравнениях с частными производными. Классические решения простейших уравнений с частными производными. Общее решение гиперболических уравнений второго порядка с двумя переменными. Рассмотр. n-мерное евклидово простр-во Опр. Множ-во ф-ций Рассмотр произв ф-цию F(x1,..,xn,z1,…,zn) Опр. Диффер ур-нием с частн производн относит ф-ции u=u(x) будем назыв рав-во: F(x,u, C помощью ф-ции F введем диффер оператор L он действует на ф-цию u: L[u]= F(x,u, Опр. Классическим решением ур-ния(1)на обл Ω назыв такую ф-цию u Из записи (1) Ур-ние (1) иногда можно записать в виде: L[u]=f(x).Такое ур-ние назывюлинейным ур-нием с частнами производнами, если для оператора L выполнены условия линейности: L[αu]=αL[u], α L[u1+u2]=L[u1]+L[u2] (3) Утвержд. Любое линейн ур-ние с частн производн порядка m имеет вид:
Т.е.L[u]= Если в ур-нии (4) ф-ция f(x)=0, то такое ур-ние наз-ся однородным, в противн случ неоднородным.
Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными. L[u]= Для классификации ур-ний введем в рассмотрение вспомогат ф-цию:D(x,y)= Опр. В зависимости от дискриминанта ур-ние (6) наз-ся: 1)гиперболическим в т.( 2)параболическим в т.( 3) эллиптическим в т.( Графически ур-ние D( Пример: 1)ур-ние колебаний струны:
2)одномерное ур-ние теплопроводности:
3)ур-ние Пуассона:
Системы. Рассмотр kнеизвестных ф-ций Опр. Системой ДУ с частными производными относит kнеизвестных ф-ций
… (1.9)
Сис-ма ур-ний (1,9) линейная, если
Классификация систем проводится аналогично как классификация уравнений.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.199.50 (0.065 с.) |
 если x
если x  , то она имеет координаты x=x(x1,…,xn). Пусть
, то она имеет координаты x=x(x1,…,xn). Пусть  . В этой обл. рассмотрим ф-цию u=u(x)=u(x1, …xn).
. В этой обл. рассмотрим ф-цию u=u(x)=u(x1, …xn). (
( наз-ся простр-вом m раз непрер-диффер ф-ций на обл Ω, т.е. u
наз-ся простр-вом m раз непрер-диффер ф-ций на обл Ω, т.е. u  (
( имеем простр-во любое число раз непрер-диффер ф-ций.
имеем простр-во любое число раз непрер-диффер ф-ций. .Будем предполагать, что существ и непрер частн производн:
.Будем предполагать, что существ и непрер частн производн:  ≠0.
≠0. .(1)
.(1) .Т.о. в результате действия оператора L на ф-цию u получаем непрерывную ф-цию.Тогда ур-ние (1)можем записать в виде: L[u]=0.
.Т.о. в результате действия оператора L на ф-цию u получаем непрерывную ф-цию.Тогда ур-ние (1)можем записать в виде: L[u]=0. что в ур-ние (1) входит производная со старшим порядком m. Поэтому будем говорить, что порядок ур-ния равен m, или степень оператора L равна m.
что в ур-ние (1) входит производная со старшим порядком m. Поэтому будем говорить, что порядок ур-ния равен m, или степень оператора L равна m. u
u  =f(x) (4)
=f(x) (4) , k-мультииндекс с координ k=(k1,k2,…,kn); |k|=k1+k1+…+kn.
, k-мультииндекс с координ k=(k1,k2,…,kn); |k|=k1+k1+…+kn. 
 +b
+b  в D, (1)
в D, (1) (2)
(2) С2;
С2; 
 ; V(D)-прос-во ф-ий u, в котором отыскивается решение задачи Коши. Для классических решений V(D)
; V(D)-прос-во ф-ий u, в котором отыскивается решение задачи Коши. Для классических решений V(D)  C2(D).
C2(D). сущ.решение задачи u
сущ.решение задачи u  ; 2) для любых нач.ф-ий
; 2) для любых нач.ф-ий  (
( +
+  . Отсюда следует существование и единственность решения задачи в прос-ве V.
. Отсюда следует существование и единственность решения задачи в прос-ве V. в области D=
в области D=  , (3)
, (3) (4). Ур-ие (3) явл-ся ур-ем типа Ковалевской, поэтому в случае аналитических ф-ий
(4). Ур-ие (3) явл-ся ур-ем типа Ковалевской, поэтому в случае аналитических ф-ий  на основании теоремы Ковалевской заключаем, что задача (3),(4) имеет единтств. аналитическое решение в некоторой достаточно малой окрестности линии Г. Т.о, первые два условия корректности выполнены. Исследуем третье условие корректности, т.е условие о непрерывной зависимости от начальных ф-ий. Для этого рассмотрим две задачи Коши с различными нач.усл. специального вида:
на основании теоремы Ковалевской заключаем, что задача (3),(4) имеет единтств. аналитическое решение в некоторой достаточно малой окрестности линии Г. Т.о, первые два условия корректности выполнены. Исследуем третье условие корректности, т.е условие о непрерывной зависимости от начальных ф-ий. Для этого рассмотрим две задачи Коши с различными нач.усл. специального вида:

 ,
,  (5)
(5)

 Введем прост-ва ф-ий V1=V2=C0A(R1), V= C0A(D), где C0A- прос-во ограниченных аналитических ф-ий.
Введем прост-ва ф-ий V1=V2=C0A(R1), V= C0A(D), где C0A- прос-во ограниченных аналитических ф-ий. (u1,u2)=
(u1,u2)= 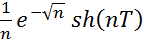 <
<  (6)
(6) Т.о., з.Коши для эллиптического ур-ия (3), (4) поставлена некорректно, т.к. не выполнено третье условие корректности из определения.
Т.о., з.Коши для эллиптического ур-ия (3), (4) поставлена некорректно, т.к. не выполнено третье условие корректности из определения. +
+  (1)
(1) (2). с нач.усл.(2), где ф-ия
(2). с нач.усл.(2), где ф-ия  -ограничена и непрерывна на
-ограничена и непрерывна на  . Решим з.Коши методом интегральных преобр.. Применим преобр. Фурье по аргументу х: U(t)=F[u]. Формально изображение U зависит не только от аргумента t, но и переменной
. Решим з.Коши методом интегральных преобр.. Применим преобр. Фурье по аргументу х: U(t)=F[u]. Формально изображение U зависит не только от аргумента t, но и переменной  . Однако эту переменную будем считать пар-ром и не вкл.ее в число аргументов ф-ии U. Используя св-ва преобр. Фурье:
. Однако эту переменную будем считать пар-ром и не вкл.ее в число аргументов ф-ии U. Используя св-ва преобр. Фурье: ]=
]= 
 ]=
]= 
 -образ ф-ии
-образ ф-ии  =(
=( )U, U(0)=
)U, U(0)=  . Получим з.Коши для обыкн. ДУ с разделяющимися перем. U(t)=
. Получим з.Коши для обыкн. ДУ с разделяющимися перем. U(t)=  -решение ДУ. Возвращаясь к з.Коши (1),(2) получим: u(t,x)=
-решение ДУ. Возвращаясь к з.Коши (1),(2) получим: u(t,x)= 
 (3)
(3)
 (4)
(4) в области
в области  , (3.2)
, (3.2)  ,
,  ,
,  , (3.3)
, (3.3) ,
,  ,
,  . (3.4)
. (3.4)
 требуется найти функцию
требуется найти функцию  , которая удовлетворяет уравнению (3.2) в области
, которая удовлетворяет уравнению (3.2) в области  , начальным условиям (3.3) и граничным условиям первого рода (3.4). ■
, начальным условиям (3.3) и граничным условиям первого рода (3.4). ■ , (3.10)
, (3.10)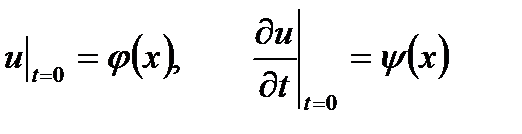 ,
,  , (3.11)
, (3.11) ,
, 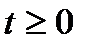 . (3.12)
. (3.12) в области
в области  , (2)
, (2)
 требуется найти функцию
требуется найти функцию  , которая удовлетворяет уравнению (2) в области
, которая удовлетворяет уравнению (2) в области  , начальному условию (3) и граничным усл первого рода (4). Функции
, начальному условию (3) и граничным усл первого рода (4). Функции  , если
, если  .
. .
. , расположенном вдоль отрезка
, расположенном вдоль отрезка  .Функция
.Функция  задает температуру стержня в сечении
задает температуру стержня в сечении  в момент времени
в момент времени  . Граничные условия (4) означают, что в торцах стержня
. Граничные условия (4) означают, что в торцах стержня  поддерживаются заданные температуры
поддерживаются заданные температуры  ,
,  . Функция
. Функция  в начальном условии (3) задает температуру стержня в каждом сечении
в начальном условии (3) задает температуру стержня в каждом сечении  в начальный момент времени
в начальный момент времени  .
. ,
,  ,
, 
 требуется найти функцию
требуется найти функцию  , которая удовлетворяет уравнению (5) в области
, которая удовлетворяет уравнению (5) в области  .
. заданы тепловые потоки.
заданы тепловые потоки. в области
в области  , (8)
, (8)
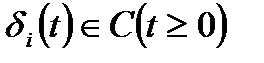 ,
,  требуется найти функцию
требуется найти функцию  , начальному условию (9) и граничным усл третьего рода (10).
, начальному условию (9) и граничным усл третьего рода (10). ,
,  .
. с окружающей средой.
с окружающей средой. +
+  +
+  +
+  +
+  +c(x,y)u=f(x,y) (6)
+c(x,y)u=f(x,y) (6) -
-  -дискриминант ур-ния (6).
-дискриминант ур-ния (6). ,
,  )
)  , если D(
, если D(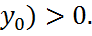

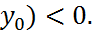
 определ некот кривую l,кот может делить обл Ω на 2 подобл
определ некот кривую l,кот может делить обл Ω на 2 подобл 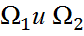 , где D>0 и D<0 соотв, тогда на
, где D>0 и D<0 соотв, тогда на  ур-ние (6) гиперболич типа, на
ур-ние (6) гиперболич типа, на  - эллиптич типа, на l –параболич типа.В этом случае будем говорить, что на всей обл Ω ур-ние (6) смешанного типа. Тогда обл
- эллиптич типа, на l –параболич типа.В этом случае будем говорить, что на всей обл Ω ур-ние (6) смешанного типа. Тогда обл  - обл эллиптичности, линия l-линияпараболичности.
- обл эллиптичности, линия l-линияпараболичности. -
-  =f(t,x)
=f(t,x) -
-  +
+  =f(t,x)
=f(t,x) ,
,  и k вспомогательных ф-ций
и k вспомогательных ф-ций 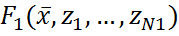 ,…,
,…,  ,обладающих св-вами аналогичными св-вам ф-ции F.
,обладающих св-вами аналогичными св-вам ф-ции F. (i=1,2,…,k) наз-ся k ур-ний:
(i=1,2,…,k) наз-ся k ур-ний: )=0
)=0 )=0
)=0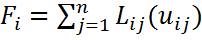 , где
, где 



