
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и ПуассонаСодержание книги
Поиск на нашем сайте
Рассмотрим ограниченную связную обл DϵRnс граничной поверхностью Г=∂D, охватывающей облD. Пусть для определенности Г Корректность задачи (19),(20),состоящей в следующем: требуется выделить пространство V граничных ф-ий φ,для котрых решение задачи Рассмотрим обл D’=R3,внешнюю по отношению к ограниченной обл D Требуется найти ф-ию u 9.Метод характеристик. Формула Даламбера для решения задачи Коши для уравнения колебаний струны. Формула Даламбера. Для отыскания решения задачи
применим метод характеристик. Метод состоит в приведении исходного уравнения (1) к каноническому виду и нахождении общего решения. Для гиперболического уравнения (1)ур. характ-к имеет вид Производя замену переменных
где Интегрируя равенство (6) по отрезку
Разрешим систему алгебраических уравнений (5), (7), тогда
После подстановки найденных функций в (4) получим формулу Даламбера для решения исходной задачи Коши:
Заметим, что найденное решение является классическим, так как В случае неоднородного уравнения колебаний струны решение задачи Коши
определяется формулой
Замечание Поставленная з. Коши опред. колебанием бесконечной струны, когда концы струны настолько удалены, что практически не влияют на процесс колебания.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.27 (0.006 с.) |

 . В обл D зададим эллиптическое ур-ие 2ого порядка с достаточно гладкими коэффициентами:L(u)=
. В обл D зададим эллиптическое ур-ие 2ого порядка с достаточно гладкими коэффициентами:L(u)= 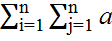 ij(
ij( +
+  i(
i( + a (
+ a ( =f(
=f( =(x1,x2,..,xn)
=(x1,x2,..,xn)  D.Потребуем, чтобы искомая ф-ия u на границе Г:u(
D.Потребуем, чтобы искомая ф-ия u на границе Г:u( =φ(
=φ( , где φ(
, где φ( , которая удовлетворяет ур-нию (17) в обл D и граничн. условию (18) на граничной поверхности Г. Задача Дирихле наз-ся также 1ой краевой задачей. Рассмотрим частный случай задачи(17),(18),когда ур-ние (17) является ур-ием Пуассона в 3-ном пространстве R3с координатами x,y,z, а обл D
, которая удовлетворяет ур-нию (17) в обл D и граничн. условию (18) на граничной поверхности Г. Задача Дирихле наз-ся также 1ой краевой задачей. Рассмотрим частный случай задачи(17),(18),когда ур-ние (17) является ур-ием Пуассона в 3-ном пространстве R3с координатами x,y,z, а обл D  R3. Внутренняя задача Дирихле. Δu
R3. Внутренняя задача Дирихле. Δu  +
+  +
+  =f(x,y,z) в обл D,(19) u(P
=f(x,y,z) в обл D,(19) u(P  =φ(P), (20) где D–ограниченная обл. Решение u(M)=u(x,y,z)
=φ(P), (20) где D–ограниченная обл. Решение u(M)=u(x,y,z) 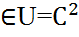 (D)
(D) 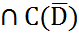 ,наз-ся классическим решением задачи (19),(20).
,наз-ся классическим решением задачи (19),(20). , единственно в пространстве U и непрерывно зависит от граничных ф-ий. Наиболее просто решаются вопросы о единственности и непрерывной зависимости. Т.1. Если решение u
, единственно в пространстве U и непрерывно зависит от граничных ф-ий. Наиболее просто решаются вопросы о единственности и непрерывной зависимости. Т.1. Если решение u  ,m≥0, a (x)≤0, граничная поверхность Г
,m≥0, a (x)≤0, граничная поверхность Г  , граничная ф-ия φ(
, граничная ф-ия φ( (Г). Пусть выполнено неравенство равномерной эллиптичности ур-ия (17):
(Г). Пусть выполнено неравенство равномерной эллиптичности ур-ия (17):  ij(
ij( ≥C
≥C 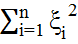 , C>0, тогда
, C>0, тогда  единственное решение задачи (17),(18) u
единственное решение задачи (17),(18) u 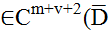 ). Из теорем следует,что в пространствах U и V задача Дирихле (19),(20) для ур-ия Пуассона поставлена корректно.
). Из теорем следует,что в пространствах U и V задача Дирихле (19),(20) для ур-ия Пуассона поставлена корректно. . Внешняя задача Дирихле в R3. Δu=f(x,y,z)(22)в облD’, u(P
. Внешняя задача Дирихле в R3. Δu=f(x,y,z)(22)в облD’, u(P  =φ(P) (23),u(M)=>0 при M->
=φ(P) (23),u(M)=>0 при M->  (D’)
(D’)  , которая удовлетворяет ур-ию (22) в облD’, граничному усл (23) и равномерно->0 на бесконечности. Задача Неймана для ур-ия Пуассона. Рассмотрим ограниченную обл D
, которая удовлетворяет ур-ию (22) в облD’, граничному усл (23) и равномерно->0 на бесконечности. Задача Неймана для ур-ия Пуассона. Рассмотрим ограниченную обл D  .Для обл D поставим краевую задачу для уравнения Пуассона, когда на поверхности Г задана производная функции u. Внутренняя задача Неймана. Δu=f(x,y,z) в D, f
.Для обл D поставим краевую задачу для уравнения Пуассона, когда на поверхности Г задана производная функции u. Внутренняя задача Неймана. Δu=f(x,y,z) в D, f  ,(25)
,(25)  ,ψ
,ψ  ,(26),где
,(26),где  -внешняя единичная нормаль к поверхности Г в точке PϵГ.
-внешняя единичная нормаль к поверхности Г в точке PϵГ. , которая удовлетвор ур-ию (25) в обл D и граничному усл(26) на граничной поверхности Г обл D.Задача Неймана называется 2ой краевой задачей. Внутр задача Неймана некорктнa,т.е. не для
, которая удовлетвор ур-ию (25) в обл D и граничному усл(26) на граничной поверхности Г обл D.Задача Неймана называется 2ой краевой задачей. Внутр задача Неймана некорктнa,т.е. не для  непрерывнх граничнх ф-ий ψ из(26)
непрерывнх граничнх ф-ий ψ из(26)  (D’)
(D’) 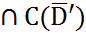 внешней задачи Неймана (29)-(31),тогда оно единственно в пространстве U.
внешней задачи Неймана (29)-(31),тогда оно единственно в пространстве U. в
в  , (1)
, (1) ,
,  , (2)
, (2) ,
,  , (3)
, (3) , а его характеристиками будут:
, а его характеристиками будут:  ,
,  .
. ,
,  ,приведем уравнение (1) к каноническому виду
,приведем уравнение (1) к каноническому виду  . Из общего решения имеем
. Из общего решения имеем  . Откуда общее решение однородного уравнения колебаний струны (1)
. Откуда общее решение однородного уравнения колебаний струны (1) . (4) Определим неизвестные функции
. (4) Определим неизвестные функции  из начальных условий. Подставив (4) в условие (2), получим соотношение
из начальных условий. Подставив (4) в условие (2), получим соотношение  . (5)Аналогично, подставляя (4) в условие (3), получаем
. (5)Аналогично, подставляя (4) в условие (3), получаем , (6)
, (6) - производные по переменной
- производные по переменной  .
.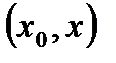 , получаем второе соотношение:
, получаем второе соотношение: (7)
(7) ,
,  .
. . (8)
. (8) для
для  .
. ,
, 
 , где
, где  .
.


