Постановка задач для уравнения денежных накоплений

Как было показано, если динамика денежных и материальных накоплений отдельной семьи подчиняется системе стохастических уравнений (6.39), где – марковский стохастический процесс с переходной функцией плотности вероятностей , которая определяется функциями , , (5.20), тогда плотность ансамбля семей в пространстве накоплений N удовлетворяет параболическому уравнению (6.54): , (6.80)где ; – эллиптический оператор. Из множества решений уравнения (6.80) необходимо найти единственное решение, которое адекватно описывает динамику накоплений выделенного множества семей (ансамбля семей), схожих по своей экономической деятельности. Для выделения единственного решения на искомую функцию необходимо наложить дополнительные условия, порождающие краевую задачу. Сформулируем некоторые краевые задачи для уравнения (6.80) по аналогии с краевыми задачами для двухмерного уравнения теплопроводности (3.26). Задача Коши на пространстве накопленийN . Предположим, что в начальный момент времени известны накопления каждой семьи. В результате с помощью соотношения (6.40) можно определить функцию плотности распределения семей на пространстве накоплений N в начальный момент времени. Получим начальное условие . (6.81)Добавив начальное условие (6.81) к уравнению (6.80), поставим задачу Коши в , (6.82) , , 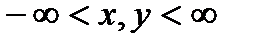(6.83) в которой требуется определить решение уравнения (6.82), удовлетворяющее условию (6.83). Смешанные задачи с нелокальными граничными условиями. Разобьем отрезок на элементарные отрезки длиной . В соответствии с формулой (6.16) на отрезке находится семей. Так как каждая семья на отрезке имеет приблизительно рублей накоплений, то в семьях на отрезке сосредоточено рублей. Суммируя по всем элементарным отрезкам, вычисляем сумму денег: , (6.72) где – сумма денег, накопленных в семьях на отрезке в момент времени . Поставим смешанную краевую задачу для уравнения денежных накоплений (6.56) на пространстве накоплений N с граничным условием (6.60) и специальным условием (6.72): в 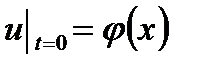, , 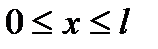, , , (6.73) где второе условие (6.73) называется нелокальным граничным условием, так как в нем задействовано не только значение функции в изолированной точке , но и значения искомой функции во всех точках отрезка . Если вместо первого условия (6.73) задано число семей в ансамбле на пространстве N в соответствии с формулой (6.17), тогда имеем задачу с двумя нелокальными граничными условиями: в , , , , , . (6.74) Заметим, что сформулированные краевые задачи требуют исследования проблемы существования и единственности решения при дополнительном условии положительности решения.