Общественный выбор в условиях прямой демократии

 

Характерные черты прямой демократии. Прямая демократия (direct democracy) — это такая политическая система, при которой каждый гражданин имеет право лич­но высказать свою точку зрения и голосовать по любому кон­кретному вопросу.

Прямая демократия сохраняется в современном обществе. Она типична для собраний коллективов предприятий и учреждений, работы клубов и творческих союзов, партийных собраний и съез­дов. В масштабе страны это проявляется в выборе депутатов пар­ламента или президента, проведении референдумов. При этом перво­степенное внимание уделяется регламенту: от того, каков принцип голосования (единогласие, простое большинство и т. д.), зависит его исход. Поэтому представителей теории общественного выбора ин­тересует основа основ — конституционный выбор, т. е. правила выбора регламента. Именно от них зависит развитие демократии. Дж. Бьюкенен и его сторонники искренне верят, что конституцион­ный регламент может сделать демократический строй более эффективным и действенным. Рассмотрим это на конкретном примере.

Модель медианного избирателя. Допустим, что жители улицы решили провести озеленение. Посадка деревьев вдоль улицы — общественное благо, для которого характерны такие свойства, как неизбирательность (неконкурент­ность) и неисключительность в потреблении.

Предположим, что вдоль улицы стоят три дома. Посадка дере­вьев, безусловно, принесет пользу всем семьям, проживающим в этих домах. Также предположим, что покупка и посадка одного дерева стоят 60 долл. Это означает, что предельные издержки в данном случае постоянны и равны 60 долл. Если они распределя­ются равномерно между всеми жильцами улицы, то каждая семья должна платить по 20 долл. Предположим, что общая выгода (TR) от посадки первого дерева составляет 180 долл., от посадки двух — 340 долл., четырех — 480 долл. и т. д. (см. табл. 14—1).

Таблица 14—1

Общая и предельная выгода от посадки деревьев (в долл.)

 

Число деревьев	Общая выгода (TR)	Предельная выгода (MR)

 

Если выгода и издержки распределяются равномерно, то будет посажено семь деревьев. Проиллюстрируем это графиком (рис. 14—1). Отложим по оси абсцисс число деревьев, а по оси ординат — пре­дельные выгоды и издержки. Функция предельных затрат посто­янна и равна 60 долл. Функция предельной выгоды убывает, она представлена прямой с отрицательным наклоном. Оптимальное число посаженных деревьев определяется в точке пересечения функции предельных выгод и предельных затрат (издержек). В данном слу­чае оно равно семи деревьям.

 

Рис. 14—1. Определение оптимального озеленения улицы (в условиях равномерного распределения издержек и выгод)

Допустим теперь, что затраты распределяются равномерно, а выгоды нет. Первая семья (Андреевых) получает 50% общей выго­ды, вторая семья (Борисовых) — 30%, а третья (Васильевых) —-20% (см. табл. 14—2).

 

Таблица 14—2

Распределение индивидуальной предельной выгоды (предельных издержек) между семьями

Число деревьев	Индивидуальная предельная выгода (предельные издержки)
Андреевы 50%	Борисовы 30%	Васильевы 20%

 

Если решения принимаются простым большинством голосов, то во втором случае (при неравномерном распределении выгод) будет посажено меньше деревьев, чем в первом. Дело в том, что для Ва­сильевых посадка уже шести деревьев будет убыточна (предель­ная выгода этой семьи от посадки шестого дерева равна 16 долл., а предельные затраты — 20 долл.). А против посадки седьмого дере­ва будут уже голосовать две семьи: Васильевых и Борисовых (так как для них предельная выгода составляет 12 и 18 долл. соответст­венно). Таким образом, если затраты распределяются равномер­но, а выгоды нет, будет иметь место недопроизводство общест­венных благ (см. MB₁ на рис. 14—2).

 

Рис. 14—2. Озеленение улицы в условиях неравномерного распределения затрат и выгод

Предположим теперь противоположный случай: когда выгоды распределяются равномерно, а издержки нет.

Допустим, что в табл. 14—2 представлены не предельные вы­годы, а предельные издержки: 50% предельных издержек несет семья Андреевых, 30% — семья Борисовых и лишь 20% — семья Васильевых. В этом случае Васильевы и Борисовы проголосуют за посадку восьми деревьев и лишь Андреевы будут против. Дело в том, что предельные выгоды (20 долл.) будут выше их предельных издержек (8 и 12 соответственно). Таким образом, если выгоды рас­пределяются равномерно, а издержки нет, будет иметь место перепроизводство общественных благ (см. МВ₂ на рис. 14—2).

Обратим внимание на то, что и во втором, и в третьем случае решающим при голосовании был голос семьи Борисовых, которые занимали место в центре. Такая ситуация получила в литературе название модели медианного избирателя.

Модель медианного избирателя (median voter model) — мо­дель, характеризующая существующую в рамках прямой демо­кратии тенденцию, согласно которой принятие решений осущест­вляется в соответствии с интересами избирателя-центриста (человека, занимающего место в середине шкалы интересов данного общества). Решение вопросов в пользу избирателя-центриста имеет свои плюсы и минусы. С одной стороны, оно удерживает сообщество от принятия односторонних решений, от крайностей. С другой — оно далеко не всегда гарантирует принятие оптимального решения.

Наш простой пример наглядно показал, что даже в условиях прямой демократии, когда решения принимаются большинством голосов, возможен выбор в пользу экономически неэффективного результата — например, недопроизводства или перепроизводства общественных благ. Дело в том, что такой механизм голосования не позволяет учесть всю совокупность выгод отдельного индивида. В рамках прямой демократии все решения сообщества имеют тен­денцию соответствовать интересам медианного избирателя, что да­леко не всегда экономически целесообразно.

Политическая конкуренция. Модель медианного избирателя имеет значение и представительной демократии, однако здесь процедура усложняется. Кандидат в президенты для того, чтобы добиться цели, должен как минимум дважды апел­лировать к избирателю-центристу: сначала внутри партии (для своего выдвижения от партии), а затем к медианному избирателю среди всего населения. При этом для завоевания симпатий боль­шинства приходится вносить значительные коррективы в свою первоначальную программу, а нередко и отказываться от ее фунда­ментальных принципов.

Рассмотрим в качестве примера распределение голосов изби­рателей в соответствии с их идеологическими предпочтениями. Отметим на горизонтальной оси позиции избирателей от крайне левых до крайне правых (рис. 14—3). В середине оси обозначим позицию медианного избирателя точкой М. Если позиции избирате­лей распределяются между крайностями в обществе равномерно, мы получим нормальное распределение с пиком над точкой М. Об­щая площадь, находящаяся под кривой, представляет 100% голосу­ющих. Допустим, что голосующие отдают свои голоса тем, кто им ближе по своим идеологическим воззрениям.

 

Рис. 14—3. Распределение голосов избирателей в соответствии с их идеологическими предпочтениями

 

Предположим, что имеются всего два кандидата. Если один из кандидатов выбирает срединную позицию (например, в точке М), то тогда он получит по крайней мере 50% голосов. Если же канди­дат занимает позицию А, то он получит меньше 50% голосов. Если один кандидат занимает позицию в точке А, а другой — в точке М, то кандидат в точке А получит голоса избирателей, находящихся левее линии а (а — срединная позиция между А и М), т. е. мень­шинство голосов. Кандидат, занимающий позицию М, сможет полу­чить голоса избирателей, находящихся правее линии а, т. е. боль­шинство. Лучшей для кандидата будет стратегия, максимально при­ближенная к позиции медианного избирателя, так как она обеспе­чит ему большинство голосов на выборах. Аналогичная ситуация сложится, если один из кандидатов будет правее другого (займет позицию в точке В). И в этом случае победа достанется тому, кто лучше отразит позицию избирателя-центриста. Проблема заклю­чается, однако, в точном определении (идентификации) интересов и чаяний медианного избирателя.

Что произойдет, если в борьбу вступит третий кандидат? Напри­мер, один кандидат занимает позицию В, а два других — позицию М. Тогда первый получит голоса, находящиеся под кривой распределе­ния правее линии b, а каждый из двух других — половину голосов, лежащих левее этой линии. Поэтому большинство голосов выиграет первый кандидат. Если один из двух кандидатов принял бы позицию А, то кандидат, занимающий позицию М, получил бы очень незначи­тельный процент голосов, равный площади, находящейся под кривой распределения между линиями а и b. Поэтому у кандидата М есть стимул выйти из сегмента АВ, тем самым он ставит одного из двух других кандидатов в затруднительное положение. Процесс продвиже­ния может долго продолжаться, но он имеет свои границы. Пока пик распределения находится в точке М, любой кандидат может повысить свои шансы, двигаясь по направлению к М.

В условиях жесткого противостояния двух различных пар­тий распределение голосов может приобрести бимодальную фор­му (рис. 14—4). В реальной действительности бимодальное распределение может иметь как симметричную (как на рис. 14—4), так и асимметричную форму (что встречается гораздо чаще).

 

 

Рис. 14—4. Бимодальное распределение голосов избирателей

 

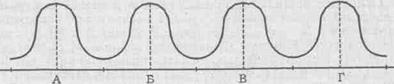
Наконец, в обществе, где отсутствует четкая поляризация инте­ресов, может встретиться и полимодальною распределение голосов избирателей. Если в таком обществе действуют четыре партии, то распределение голосов может приобрести (в идеале) такую форму, которая показана на рис. 14—5. На рисунксе изображено равномер­ное распределение голосов между партиями. Однако это частный случай. Здесь также возможен асимметричный сдвиг вправо или влево.

 

Рис. 14—5. Полимодальное распределению голосов избирателей

 

Представленные модели политической конкуренции довольно абстрактны, но они все-таки позволяют шрояснить факторы, дви­жущие политическим поведением кандидатов.