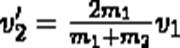Применение законов сохранения К абсолютно неупругому удару. Энергия идущая на деформацию. Применение неупругого удара.

Удар абсолютно упругих и неупругих тел является примером применения законов сохранения импульса и энергии при решении физической задачи.

Соударение тел – столкновение двух или более тел, при которых взаимодействие длится очень короткое время.

При ударе тела испытывают деформацию. Понятие удара подрузамевает, что кинетическая энергия относительного движения ударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Опыты показывают, что относительная скорость тел после соударения не достигает своего значения до соударения. Это объясняется тем, что не бывает идеально упругих тел и идеально гладких поверхностей. Отношение нормальной составляющей относительной скорости тел после удара к нормальной составляющей относительной скорости тел до удара называется коэффициентом восстановления ε: ε = νn'/νn

Если для соударяющихся тел ε=0, то такие тела называются абсолютно неупругими, если ε=1 - абсолютно упругими. На практике для всех тел 0<ε<1 (например, для шаров из слоновой кости ε=0,89; для стальных шаров ε=0,56, для свинца ε≈0). Но в некоторых случаях тела можно с большой степенью точности рассматривать либо как абсолютно неупругие, либо как абсолютно упругие.

Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай).

Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса.

Абсолютно неупругий удар - соударение двух тел, в результате которого тела соединяются, двигаясь дальше как единое целое. Абсолютно неупругий удар можно продемонстрировать с помощью шаров из пластилина (глины), которые движутся навстречу друг другу

Вследствие деформации происходит уменьшение кинетической энергии, которая переходит в тепловую или другие формы энергии. Это уменьшение можно определить по разности кинетической энергии тел до и после удара

 

13 вопрос

Применение законов сохранения к абсолютно упругому удару. Частные случаи (m1=m2; m2>>m1) и их конкретные проявления.

Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай).

Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса.

Обозначим скорости шаров массами m1 и m2 до удара через ν1 и ν2, после удара - через ν1' и ν2' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.

При указанных допущениях законы сохранения имеют вид

 

1. При ν2=0

Проанализируем выражения (8) в (9) для двух шаров различных масс:

а) m1=m2. Если второй шар до удара висел неподвижно (ν2=0) (рис. 2), то после удара остановится первый шар (ν1'=0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (ν2'=ν1);

m2>>m1 (например, столкновение шара со стеной). Из уравнений (8) и (9) следует, что ν1'= -ν1; ν2' ≈ 2m1ν2'/m2.

2. При m1=m2 выражения (6) и (7) будут иметь вид ν1'= ν2; ν2'= ν1; т. е. шары равной массы как бы обмениваются скоростями.

 

14 вопрос