
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отступление от законов идеального газа. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РЕА́ЛЬНЫЙ ГАЗ - газ, свойства которого существенно зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная энергия взаимодействия молекул много меньше их средней кинетической энергии, свойства реальных газов незначительно отличаются от свойств идеального газа и к реальным газам применимы законы, установленные для идеального газа. Отличие свойств реального газа от свойств идеального становится особенно значительным при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты.
В модели идеального газа не учитывается собственный объем молекул и силы межмолекулярного взаимодействия. Тщательная экспериментальная проверка газовых законов (закон Бойля —Мариотта, закон Шарля, закон Гей-Люссака) современными методами показала, что эти законы достаточно точно описывают поведение реальных газов при небольших давлениях и высоких температурах. При других условиях наблюдаются значительные отступления от этих законов. Причина заключается в том, что, во-первых, при очень сильном сжатии газов объем незанятого молекулами пространства становится сравним с объемом, занимаемым самими молекулами; а во-вторых, при низких температурах становится заметным взаимодействие между молекулами. Поэтому для описания поведения газа при достаточно больших плотностях (больших давлениях) уравнения состояния идеального газа не пригодны. Наличие сил межмолекулярного взаимодействия, а именно сил отталкивания, действующих на малых расстояниях порядка размеров молекул, и сил притяжения, приводит к сложной зависимости энергии потенциального взаимодействия молекул от расстояния.
Для описания термодинамических свойств реальных газов используются различные уравнения состояния. При малых плотностях наличие межмолекулярного взаимодействия учитывается вириальным уравнением состояния реального газа:
pV = RT[1 + B(T)/v + C(T)/v2 +...],
где p — давление, v — мольный объем, Т — абсолютная температура, R — газовая постоянная, В(Т), С(Т) и т. д. — вириальные коэффициенты, зависящие от температуры и характеризующие парные, тройные и т. д. взаимодействия частиц в газе. Качественно верно описывает основные отличия реального газа от идеального уравнение Ван-дер-Ваальса, учитывающее существование сил притяжения между молекулами, действие которых приводит к уменьшению давления газа, и сил отталкивания, препятствующих безграничному сжатию газа.
Кроме уравнения Ван-дер-Ваальса было предложено много других эмпирических уравнений состояния реальных газов. Некоторые из них дают лучшее согласие с опытом за счет большого числа входящих в них феноменологических постоянных. Однако при качественном исследовании поведения реальных газов использование уравнения Ван-дер-Ваальса более удобно, благодаря его простоте и понятному физическому смыслу.
Одной из основных характеристик реальных газов являются размеры молекул. В реальных газах их называют газокинетическими радиусами, и их размер связан с характерными расстояниями, на которых проявляются силы межатомных и межмолекулярных взаимодействий.
40 вопрос Уравнение Ван-дер-Ваальса ВАН-ДЕР-ВААЛЬСА УРАВНЕ́НИЕ, уравнение состояния, описывающее свойства реального газа. Предложено Й. Д. Ван-дер-Ваальсом в 1873 г. Широко используется для качественного анализа поведения реальных газов и жидкостей. В модели реального газа Ван-дер-Ваальса молекулы рассматриваются как абсолютно твердые слабо притягивающиеся упругие сферы определенного диаметра.
Уравнение Ван-дер-Ваальса количественно определяет свойства реальных газов лишь в небольшом интервале температур и давлений: в области относительно высоких температур и низких давлений, так как входящие в него экспериментально определяемые константы являются функциями температуры.
Для моля газа объемом V при температуре Т и давлении р, уравнение Ван-дер-Ваальса имеет вид:
(p+a/Vm 2)(Vm - b) = RT,
где: R — газовая постоянная,
a и b — экспериментальные константы, учитывающие отклонение свойств реального газа от свойств идеального газа.
Член a/V2 имеет размерность давления и учитывает притяжение между молекулами газа за счет ван-дер-ваальсовых сил. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е. рвн = a/Vm2, где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm — молярный объем.
Константа b является поправкой на собственный объем молекул газа и учитывает отталкивание молекул на близких расстояниях. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, приводит к тому, что фактически свободный объем, в котором будут двигаться молекулы реального газа, будет не Vm, а Vm-b, где b — объем, занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул.
Константы а и b обычно определяются из экспериментальных данных, и эти величины постоянны для каждого газа. Для их определения записывают уравнения для двух известных из опыта состояний газа и решают эти уравнения относительно а и b. При больших объемах V можно пренебречь обеими поправками и уравнение Ван-дер-Ваальса переходит в уравнение состояния идеального газа (см. Клапейрона уравнение).
Несмотря на то, что уравнение Ван-дер-Ваальса является приближенным и количественно описывает свойства реальных газов лишь в области высоких температур и низких давлений, качественно оно позволяет описывать поведение газа и при высоких давлениях, конденсацию газа в жидкость. Уравнение Ван-дер-Ваальса также описывает критическое и метастабильное состояние системы жидкость-пар.
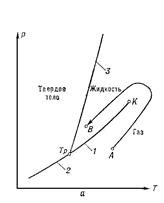
41 вопрос Сравнение изотерм Ван-дер-Ваальса с экспериментальными. Критическое состояние. Изотермы Ван-дер - Ваальса на pF - диаграмме с повышением температуры поднимаются вверх. Это сопровождается сближением объемов YI и F2 определяющих соответственно объемы жидкой и газообразной фазы. Совпадение жидкой и газообразной фазы произойдет в точке А (см. рис. 10), которая называется критической. Эта точка определяется точкой перегиба изотермы, температура которой называется критической.
Изотерма Ван-дер - Ваальса, соответствующая критической температуре Ткр вещества, имеет точку перегиба - критическую точку.
Сравнение изотерм Ван-дер - Ваальса (см. рис. 13.7) с эксперя-ментальными изотермами реальных веществ (например, с рис. 13) показывает, что изотермы Ван-дер - Ваальса охватывают не только область газообразного состояния вещества, но также области двухфазного и жидкого состояний. Жидкому состоянию соответствуют круто уходящие вверх левые участки изотерм. Однако в этой области имеется лишь качественное согласие с результатами экспериментов. Сравнение изотерм Ван-дер - Ваальса (рис. 12.7) с экспериментальными изотермами реальных веществ (например, с рис. 12.5) показывает, что изотермы Ван-дер - Ваальса охватывают не только область газообразного состояния вещества, но также области двухфазного и жидкого состояний. Жидкому состоянию соответствуют круто уходящие вверх левые участки изотерм. Однако в этой области имеется лишь качественное согласие с результатами экспериментов.
КС Критическое состояние 1) предельное состояние равновесия двухфазных систем, в котором обе сосуществующие фазы (См. Фаза) становятся тождественными по своим свойствам; 2) состояние вещества в точках фазовых переходов (См. Фазовый переход) II рода. К. с., являющееся предельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесии жидкость — газ, а в растворах — при фазовых равновесиях (См. Фазовое равновесие) газ — газ, жидкость — жидкость, жидкость — газ, твёрдое тело — твёрдое тело. На диаграммах состояния (См. Диаграмма состояния) К. с. соответствуют предельные точки на кривых равновесия фаз (рис. 1, а и б) — т. н. критические точки (См. Критическая точка). Согласно фаз правилу (См. Фаз правило) критическая точка изолирована в случае двухфазного равновесия чистого вещества, а, например, в случае бинарных (двойных) растворов (См. Растворы) критические точки образуют критическую кривую в пространстве термодинамических переменных (параметров состояния). Значения параметров состояния, соответствующие К. с., называются критическими — критическое давление рк, критическая температура Тк, критический объём Vк, критический состав хк и т. д.
С приближением к К. с. различия в плотности, составе и др. свойствах сосуществующих фаз, а также теплота фазового перехода и межфазное поверхностное натяжение уменьшаются и в критической точке равны нулю. В том случае, когда кривая сосуществования фаз заканчивается критической точкой, оказывается принципиально возможным перевести вещество из одной фазы в другую, минуя область расслоения на две фазы (например, газ превратить в жидкость, изменяя его состояние по линии AB на рис. 1, а, т. е. минуя область, где одновременно существуют газ и жидкость). Сжижение (конденсацию) газов возможно осуществить лишь после их охлаждения до температур, меньших Тк. В двухкомпонентных системах характерные для К. с. явления наблюдаются не только в критической точке равновесия жидкость — газ, но и в так называемых критических точках растворимости, где взаимная растворимость компонентов становится неограниченной. Существуют двойные жидкие системы как с одной, так и с двумя критическими точками растворимости — верхней и нижней (рис. 2, а и б). Эти точки являются температурными границами области расслаивания жидких смесей на фазы различного состава. Аналогичной способностью к расслаиванию при определённой критической температуре обладают некоторые растворы газов и Твёрдые растворы. Переход системы из однофазного состояния в двухфазное вне критической точки и изменение состояния в самой критической точке происходят существенно различным образом. В первом случае при расслоении на две фазы переход начинается с появления (или исчезновения) бесконечно малого количества второй фазы с конечным отличием её свойств от свойств первой фазы, что сопровождается выделением или поглощением теплоты фазового перехода. Поскольку возникновение такой новой фазы приводит к появлению поверхности раздела и поверхностной энергии, для её рождения требуются достаточно большие зародыши. Это означает, что при таком фазовом переходе (фазовом переходе 1 рода) возможны переохлаждение или перегрев первой фазы, обусловленные отсутствием жизнеспособных зародышей новой фазы.
Фазовые переходы в критических точках, являющихся предельными на кривых равновесия фаз, представляют собой частные случаи фазовых переходов II рода. В критической точке фазовый переход происходит в масштабах всей системы. Флуктуационно возникающая новая фаза по своим свойствам бесконечно мало отличается от свойств исходной фазы. Поэтому возникновение новой фазы не связано с поверхностной энергией, т. е. исключается перегрев или переохлаждение, и фазовый переход не сопровождается выделением или поглощением теплоты и скачком удельного объёма (фазовый переход II рода). При приближении к К. с. физические свойства вещества резко изменяются: теоретически неограниченно возрастает теплоёмкость и восприимчивость системы к внешним воздействиям (например, изотермическая сжимаемость в случае чистых жидкостей, магнитная восприимчивость у ферромагнетиков и т. д.); наблюдается целый ряд др. особенностей в поведении вещества (см. Критические явления). Эти особенности, характерные для К. с. объектов самой различной природы, объясняются тем, что свойства вещества в К. с. определяются не столько конкретными законами взаимодействия его частиц, сколько резким возрастанием в веществе флуктуаций и радиуса их корреляции. Знание особых свойств веществ в К. с. необходимо во многих областях науки и техники: при создании энергетических установок на сверхкритических параметрах, сверхпроводящих систем, установок для сжижения газов, разделения смесей и т. д.
Рис. 1. а — диаграмма состояния чистого вещества в координатах р, Т. Кривые сосуществования обозначены цифрами: 1 — равновесие жидкость — газ, 2 — твёрдое тело; 3 — твёрдое тело — жидкость; К — критическая точка, Т = Тк — критическая изотерма; б — диаграмма в координатах р, V. Цифрами обозначены области сосуществования двух фаз: 1 — жидкость — газ; 2 — твёрдое тело — газ; 3 — твёрдое тело — жидкость.
Рис. 2. а — верхняя критическая точка (Кв) жидкой смеси фенол — вода (Tк ≈ 66°С). Заштрихована область, где смесь состоит из двух фаз, имеющих различную концентрацию компонентов; б — двухкомпонентная жидкая система никотин — вода, имеющая как верхнюю критическую точку растворения (Кв с Tк = 208°С), так и нижнюю критическую точку (Кн с Тк ≈ 61° С).
42 вопрос Фазовые переходы I и II рода.Уравнение Клапейрона-Клаузиуса. Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в которой лед является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях — фазах). Переход вещества из одной фазы в другую — фазовый переход — всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую).
Различают фазовые переходы двух родов. Фазовый переход I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы I рода характеризуются постоянством температуры, изменениями энтропии и объема. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. В подобных переходах — из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние — степень беспорядка увеличивается, т. е., согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.
Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объема, называются фазовыми переходами II рода. Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Общая трактовка фазовых переходов II рода предложена академиком Л. Д. Ландау (1908—1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов II рода являются: переход ферромагнитных веществ (железа, никеля) при определенных давлении в температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия (гелия I) при Т=2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести.
Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением
43 вопрос Внутренняя энергия реального газа. Эффект Джоуля-Томсона. Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул и из потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ.
р΄=а/V2
Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, или, иными словами, против внутреннего давления, как известно из механики, идёт на увеличение потенциальной энергии системы.
Т.е. dA=p΄Vm=dП, или dП=a/V2m*dVm, откуда П=-а/Vm.
Знак минус означает, что молекулярные силы, создающие внутреннее давление р΄, являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа Um=CVT-a/Vm растёт с повышением температуры и увеличением объёма.
Если газ расширяется без теплообмена с окружающей средой и не совершает внешней работы, то на основании первого начала термодинамики получим, что U1=U2. Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется.
Эффе́ктом Джо́уля — То́мсона называется изменение температуры газа при адиабатическом дросселировании — медленном протекании газа под действием постоянного перепада давлений сквозь дроссель (пористую перегородку). Данный эффект является одним из методов получения низких температур. Изменение энергии
Изменение энергии газа в ходе этого процесса будет равно работе:
Следовательно, из определения энтальпии
следует, что процесс изоэнтальпиен. Изменение температуры
Изменение температуры при малом изменении давления (дифференциальный эффект) в результате процесса Джоуля — Томсона определяется производной
называемой коэффициентом Джоуля — Томсона. С помощью элементарных преобразований можно получить выражение для этого коэффициента:
Где
Если при протекании газа через пористую перегородку температура возрастает ( ( Применение Процесс Джоуля — Томсона используют для получения низких температур. Для этой цели обычно применяют интегральный процесс, при котором давление изменяется в широких пределах. Измерение позволяет установить уравнение состояния газа.
44 вопрос
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 679; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.015 с.) |









 теплоёмкость при постоянном давлении. Для идеального газа
теплоёмкость при постоянном давлении. Для идеального газа  а для реального газа он определяется уравнением состояния.
а для реального газа он определяется уравнением состояния. ) то эффект называют отрицательным, и наоборот, если температура убывает
) то эффект называют отрицательным, и наоборот, если температура убывает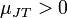 ) то процесс называют положительным. Температуру, при которой меняет знак, называют температурой инверсии.
) то процесс называют положительным. Температуру, при которой меняет знак, называют температурой инверсии.


