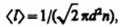Закон Больцмана для распределения частиц во внешнем потенциальном поле.

Заменив в Барометрической формуле p через nkT получим закон изменения концентрации газа с высотой:

Где n₀ – концентрация газа на высоте h=0

Преобразуем, заменив M/R равным ему отношению m₀/k

Где m₀ - масса одной молекулы, k – постоянная Больцмана

С уменьшением температуры концентрации газа на высотах отличных от нуля, убывает, обращаясь в ноль при температуре T=0

При абсолютном нуле все молекулы воздуха расположились бы на земной поверхности.

При больших температурах наоборот концентрация слабо уменьшается с высотой.

Распределение молекул газа получается в результате действия двух «конкурирующих» тенденций: 1. притяжение к земле, 2. тепловое движение

На разной высоте молекула обладает разной потенциальной энергией => распределение молекул газа по высоте, является в тоже время распределением их по значениям потенциальной энергии.

Таким образом получаем:

Из этого => что молекулы располагаются с большей концентрацией (плотностью) тела, где их потенциальная энергия меньше, и наоборот, с меньшей плотностью в местах, где их потенциальная энергия больше.

 

32 вопрос

Среднее число столкновений и средняя длина свободного пробега молекул.

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул <l>.

 

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 68). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).

 

Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости <v>, и если <z> — среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега

Для определения <z> представим себе молекулу в виде шарика диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. 69).

 

Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра:

где n — концентрация молекул, V = pd2 <v> <v> — средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом, среднее число столкновений

Расчеты показывают, что при учете движения других молекул

Тогда средняя длина свободного пробега

т. е. <l> обратно пропорциональна концентрации n молекул. С другой стороны, из (42.6) следует, что при постоянной температуре n пропорциональна давлению р. Следовательно,

 

33 вопрос