
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциального кинетического уравненияСодержание книги
Поиск на нашем сайте Определим константы дифференциального кинетического уравнения для следующей реакции: аА + bB → продукты. Зависимость скорости от концентраций выражается уравнением (4.3):
Прологарифмируем это выражение
Так как величины k, n и m для рассматриваемой реакции (при T =const) являются постоянными и не зависят от концентрации реагентов, то для их нахождения достаточно определить зависимость скорости реакции от концентрации одного из реагентов при фиксированной концентрации другого реагента. Пусть в трех опытах концентрация вещества А будет постоянной и равной [ A ]0. Тогда в уравнении (4.4) сумма ( Обозначим ее Тогда уравнение (4.4) можно переписать как
Зависимость (4.5) представляет собой в координатах ln[ B ] – По экспериментальным данным строят график зависимости
В последующих опытах определяют скорость реакции при различных исходных концентрациях вещества А и постоянной концентрации [ B ]0. Находят порядок реакции по веществу А
Из уравнения (4.3) с учетом найденных порядков реакции по веществам А и В рассчитывают константу скорости
где
Рис. 4.2. Определение порядка реакции по веществу В Зависимость концентрации реагирующих веществ От времени для реакции первого порядка. Интегральное кинетическое уравнение На практике чаще всего интересует не само значение скорости химической реакции, а то, сколько вещества израсходовано или образовалось к определенному моменту времени после начала реакции. Рассмотрим эту задачу на примере реакции первого порядка: А ® продукты. Скорость такой реакции выражается следующим уравнением:
В дифференциальном виде
Перепишем это уравнение в следующем виде:
и возьмем определенный интеграл от обеих частей уравнения от исходного состояния ([ A ]0, t 0 = 0) до текущего момента ([ A ]t, t):
Решение этого уравнения приводит к следующей зависимости:
или
Соотношения (4.8) и (4.9) являются интегральными кинетическими уравнениями реакции первого порядка. Зная исходную концентрацию вещества [ A ]0 и константу скорости реакции k, можно рассчитать концентрацию [ A ]t через любое время t после начала реакции. Если же известны исходная концентрация [ A ]0 и концентрация реагирующего вещества [ A ]t через какое-то время t после начала реакции, то можно рассчитать константу скорости этой реакции
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 .
. .
.
 ) будет тоже величиной постоянной.
) будет тоже величиной постоянной.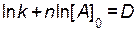 .
. .
.
 уравнение прямой линии, тангенс угла наклона которой к оси абсцисс численно равен порядку реакции по веществу В.
уравнение прямой линии, тангенс угла наклона которой к оси абсцисс численно равен порядку реакции по веществу В. .
. .
. ,
, , [ A ] i, [ B ] i – экспериментальные данные, относящиеся к одному опыту.
, [ A ] i, [ B ] i – экспериментальные данные, относящиеся к одному опыту.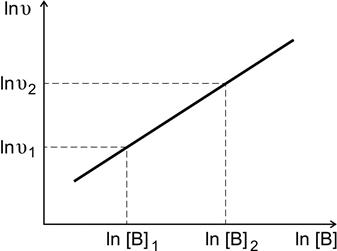
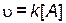 .
.
 .
.


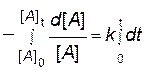 .
.
 .
.
 .
.



