
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый закон термодинамики. Понятие об энтальпииСодержание книги
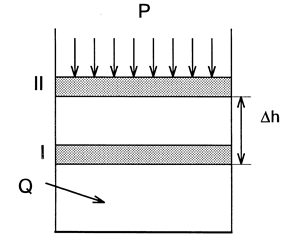
Поиск на нашем сайте Первый закон термодинамики является частным случаем закона сохранения энергии применительно к процессам, в которых выделяется, поглощается или преобразуется тепловая энергия. Рассмотрим, как изменяется внутренняя энергия ∆U при проведении процесса, в котором система (газ, находящийся при постоянном давлении р =const в цилиндре под поршнем) (рис. 3.1), получает некоторое количество тепловой энергии Q р, в результате чего газ нагревается (Т 2> T 1, U 2> U 1) и расширяется (V 2> V 1). Если положение поршня не зафиксировано, то поршень будет перемещаться до тех пор, пока внешняя сила F (F = p.s), приложенная к поршню, не уравновесит силу, действующую на поршень со стороны системы. Тогда имеем F = p.s, где p – внешнее давление, s – площадь поперечного сечения цилиндра.
Рис. 3.1. К выводу первого закона термодинамики При этом движении совершается работа против сил внешнего давления, равная A = F . ∆h, где ∆h – величина перемещения поршня. Поскольку произведение площади поперечного сечения цилиндра на величину перемещения поршня есть приращение объема системы ∆V, то можно записать
Тепловая энергия, сообщенная газу, при постоянном давлении Q р идет частично на увеличение внутренней энергии ∆U, а частично на производство работы A (при p =const): − Q p= ∆U + A = ∆U + p∆V. (3.1) Данное уравнение представляет собой термохимическую запись. Знак минус перед теплотой (− Q p) в уравнении (3,1) соответствует теплоте, подведенной к системе. Уравнение (3.1) является аналитическим выражением первого закона термодинамики: количество теплоты, сообщенное системе, расходуется на увеличение ее внутренней энергии и на совершение системой работы. Учитывая, что ∆U = U 2− U 1, а ∆V = V 2− V 1, уравнение (3.1) запишется в виде: − Q р= U 2− U 1+ р (V 2− V 1)=(U 2+ рV 2)−(U 1+ рV 1)= Н 2− Н 1= ∆Н. (3.2) Сумма внутренней энергии и произведения давления на объем (H = U + pV) получила название энтальпии (∆Н) или энергосодержания. Энтальпия является функцией состояния. Свойства энтальпии: 1. Разность энтальпий системы в конечном и начальном состояниях не зависит от пути перехода системы из одного состояния в другое. 2. Энтальпия системы равна сумме энтальпий частей, составляющих систему, т.е. энтальпия − величина аддитивная. 3. Абсолютное значение энтальпии системы является принципиально неопределяемым. Поэтому обычно пользуются относительными значениями энтальпий ∆Н, причем за точку отсчета принимают значение энтальпии образования простых веществ при 298 К (25оС), давлении 101,3 кПа (1атм), если они при этих условиях, называемых стандартными, находятся в устойчивом состоянии. Стандартные энтальпии образования всех простых веществ, устойчивых в стандартном состоянии, равны нулю. Например, ∆Н о298,Н2(газ)=0 кДж/моль. Энтальпия сложного вещества − стандартная энтальпия образования, которая равна количеству теплоты с обратным знаком, выделяющейся или поглощающейся при образовании одного моля вещества из простых веществ, находящихся в устойчивых агрегатных состояниях в стандартных условиях. Стандартные энтальпии образования определены для большого числа веществ и сведены в таблицы термодинамических величин (см. Прил. Табл. 2), измеряются в кДж/моль. Для расчета энтальпий в нестандартных условиях (например, р =101,3 кПа, Т В пределах одного фазового состояния (газового, жидкого и т.д.) изменение энтальпии при изменении температуры невелико, но при фазовых переходах изменение энтальпии происходит скачкообразно на величину соответственно теплоты плавления ∆Н пл или парообразования (кипения) ∆Н кип, взятых с обратным знаком. Уравнение температурной зависимости энтальпии моля вещества в пределах одного фазового состояния:
где Сp – мольная теплоемкость при постоянном давлении, которая равна количеству теплоты, необходимому для нагревания 1 моля вещества на один градус.
Рис. 3.2. Зависимость энтальпии образования вещества от температуры Ср зависит от природы и агрегатного состояния вещества, а также от температуры. Однако в небольшом температурном интервале зависимостью Ср от температуры можно пренебречь и считать, что ∆Н = Ср · ∆Т. С помощью этого соотношения можно рассчитать энтальпии веществ для различных температур (в пределах одного агрегатного состояния).
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.005 с.) |

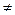 298 К) используют зависимость энтальпии от температуры (рис. 3.2).
298 К) используют зависимость энтальпии от температуры (рис. 3.2).




