
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Керченский государственный морской технологическийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ (ФГБОУ ВО «КГМТУ») Морскойфакультет Кафедра «Судовождение и промышленное рыболовство»
МАТЕМАТИЧЕСКИЕ ОСНОВЫ СУДОВОЖДЕНИЯ
КОНСПЕКТ ЛЕКЦИЙ ДЛЯ КУРСАНТОВ СПЕЦИАЛЬНОСТИ 26.05.05 «СУДОВОЖДЕНИЕ» ОЧНОЙ И ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Керчь, 2016 г.
СОДЕРЖАНИЕ
Стр. Введение 5 РАЗДЕЛ 1 ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ ВОЖДЕНИЯ МОРСКОГО СУДНА 7 1.1 Навигационный сигнал как носитель навигационной информации 7 1.2 Навигационное пространство и элементы движения судна 22 1.3 Навигационные параметры, их измерения, классификация методов и средств 24
РАЗДЕЛ 2 ГЕОМЕТРИЯ ЗЕМНОГО СФЕРОИДА 38 2.1 Геоид, апиоид, референц-эллипсоиды 38 2.2 Системы координат и направлений 41 2.3 Главные радиусы кривизны, длины дуг 46 2.4 Геодезическая линия и локсодромия 52 2.5 Прямая и обратная геодезические задачи 56
РАЗДЕЛ 3 МАТЕМАТИЧЕСКАЯ КАРТОГРАФИЯ 64 3.1 Основные понятия и определения 64 3.2 Элементы общей теории искажений 66 3.3 Картографические проекции 68 3.4 Равноугольная цилиндрическая проекция 71 3.5 Построение промыслово-навигационного планшета в меркаторской проекции. 73
РАЗДЕЛ 4 ТЕОРИЯ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА С ОЦЕНКОЙ ТОЧНОСТИ 77 4.1 Способы определения места судна 77 4.2 Графоаналитический метод 82 4.3 Влияние случайных ошибок измерений на точность определяемого по двум ЛП места 86 4.4 Графические методы отыскание вероятнейшего места судна при избыточном числе линий положения. 90 4.5 Общий случай построения эллипса погрешностей 98 4.6 Аналитическое определение места судна с оценкой точности 100
РАЗДЕЛ 5 ИСПОЛЬЗОВАНИЕ РАЗНОВРЕМЕННЫХ ЛП 107 5.1 Общий случай решения основной задачи судовождения 107 5.2 Метод исправленного крюйс-пеленга 110 5.3 Общий случай СЛП 113 5.4 Частные случаи применения СЛП 116 РАСЧЕТЫ БЕЗОПАСНОСТИ МОРЕПЛАВАНИЯ 118 6.1. Особенности проблемы 118 6.2. Основные способы определения вероятности безаварийной работы судов 121 6.3. Количественная оценка безопасности плавания судна вблизи навигационной опасности 124 6.4. Влияние технического состояния навигационных приборов судна на безопасность плавания 129
6.5. Выводы 136 Литература 138
ВВЕДЕНИЕ
Эффективное управление современными крупнотоннажными промысловыми и транспортными судами возможно лишь специалистами, которые прошли хорошую морскую школу и в совершенстве владеют новейшими методами и средствами судовождения. Поэтому современный инженер-судоводитель должен владеть глубокими теоретическими знаниями в избранной специальности и иметь хорошую математическую подготовку. «Математические основы судовождения» являются теоретической базой для ряда специальных дисциплин: навигации, лоции, мореходной астрономии, автоматизации судовождения. Данный курс предполагает углубленное изучение теоретических основ выбора пути и определения места судна, а также знакомство с некоторыми общими подходами к решению штурманских задач. Предмет “Математические основы судовождения” не исключает основные профилирующие дисциплины, а, наоборот, предполагает развитие и углубление излагаемых в нем вопросов на основе знаний практически всех специальных дисциплин. Современное судовождение немыслимо без знания основ теории вероятностей, поскольку особенности проявления случайных событий и величин являются основой практической работы судоводителя. Он должен владеть методикой обработки наблюдений с оценкой их точности. Более того, с появлением комплексных навигационных систем, необходимо знать методы приведения результатов измерений в формальное согласие, т.е. методы уравнивания измерений. Широко применяемый в аналитических расчетах метод наименьших квадратов позволяет решать основную задачу судовождения - определение места судна аналитическим путем и с оценкой точности. Внедрение на судах вычислительной техники и автоматизированных средств судовождения требует от судоводителей глубоких знаний не только теории движения судна, но и математического описания этих процессов на поверхности земли, имеющей сложную форму. Основной задачей курса является подготовка судоводителя к решению специальных задач судовождения на высоком теоретическом уровне с использованием достижений современной науки и вычислительной техники в соответствии с требованиями правила А-II/2 Кодекса ПДМНВ.
В конспект лекций включен минимальный круг вопросов, предусмотренный программой курса по следующим разделам: «Способы и приемы штурманских вычислений», «Сферическая тригонометрия», «Геометрия земного сфероида на плоскости». Данный конспект лекций не заменяет существующего учебника (Кожухов В.П., Григорьев В.В., Лукин С.М. «Математические основы судовождения» - М.: Транспорт, 1987.-208 с.), а лишь служат дополнительным пособием, в котором предложены другие способы доказательства ряда формул и материал изложен более кратко. С целью сокращения объема пособия в нем не приводятся числовые примеры решения задач. Они подробно рассмотрены в Методических указаниях к проведению практических занятий по данной дисциплине и в названном выше учебнике. Цели и задачи курса, а также необходимые знания и умения студентов, приобретенные после изучения этой дисциплины, приведены в рабочей программе дисциплины «Математические основы судовождения».
РАЗДЕЛ 1 Общие положения
Трудно переоценить значение современного судовождения в решении задач по выполнению планов современной экономики, в обеспечении безопасных и экономичных переходов судов между пунктами на земной поверхности, в той огромной ответственности судоводителя за сохранность человеческиз жизней и материальных ценностей, которые возлагаются него как на специалиста. Чтобы в полной мере ответить на эти вопросы, следует обобщенно рассмотреть весь цикл наук «Судовождение» и указать круг задач, решаемых этим циклом; затем выделить такие науки, как навигация, лоция и промысловая навигация, управление судном и маневрирование, мореходная астрономия, технические средства судовождения, автоматизация процессов судовождения, навигационная гидрометеорология и картография. Любую из этих учебных и научных дисциплін нужно рассматривать, указывая и мотивировано учитывая круг задач любой из них. Все эти дисциплины являються базой математияческих основ судовождения, которая обобщает и систематизирует реальне факты и математические положення, лежащие в основе наук судоводительского цикла, и призвана воспитывать у будущих специалистов необходимый кругозор и широту навигационного мышления, диалектического единства методов судовождения и общность их теоретического фундамента. Базируясь на всех дисциплинах судоводительского цыкла, математические основы судовождения формируют понятия навигационного пространства в виде сфероидической, сферической и плоской модели Земли; систем координат, кото
рые строяться на этих моделях; геодезических задач, решаемых с помощью систем координат; навигационных задач, к которым сводятся геодезические, то есть рассмотреть геодезическую основу судовождения. Затем в общем виде рассматриваются вопросы вождения подвижных обьектов с указанем навигационнх элементов их движения; навигационных параметров, не зависящих от движения удна и составляющих основу обсерваций; навигацонных изолиний и методов их расчета; картографических проекцій, особо выделив меркаторскую; обобщенного метода линий положення – основного в современной практике метода косвенной обработки навигационных параметров; прямих аналитических методов обработки навигационных параметров, позволяющих использовать вычислительную технику, общие вопросов оценки точности счисления и обсерваций, полученных по измерениям любого числа независимых навигационных параметров.
Современная литература по судовождению не имеет полных готових ответов на все перечисленные вопросы в комплексе. Изучение материала требует логического обобщения знаний всех дисциплін цикла судовождение применительно к проблеме обеспечения безопарного плавання судов в конкретних условиях. При этом обьязательно должны использовать современые достижения науки и техники, учитывая постоянное обогащение судовождения за сет фундаментальних наук и наук естественно-географического цикла. Носителем навигационной информации является навигационнй сигнал. В современных средствах судовождения в качествет навигационных сигналов используются электромагнитные колебания, а также механические и электрические возмущения, завсящие от измеряемого навигационного параметра. В автоматизированных навигационных комплексах обработке подлежат Следует знать и четко представлять значение навигационного сигнала для получения навигационной информации. Навигационный сигнал является неотъемлемой частью любой навигационной системы и источником для виработки нави
гационной информации. В качестве навигационного сигнала может использоваться либо какой-нибудь физический процесс, происходящий и распространяющийся в пространстве, либо каное нибудь материальное движущееся тело. Практикой судовождения к навигационному сигналу предъявлются определенные требованиия, выполнение которых открывает широкие возможности использования его в навигационных целях.
Вопросы для самопроверки 1. Что изучает наука «Математические основы судовождения»? Какой круг задач она решает? 2. Какие новые достижения фундаментальных наук используются в судовождении? 3. Что такое навигационная информация? Где она формируется? 4. Что такое навигационный сигнал? Какие требования к нему предъявляются? 5. Какие виды навигационного пространства применяют в судовождении?
6. В каких средах происходит движение судна и как они влияют на него? 7. Какие параметры движения судна и навигационные параметры используют в судовождении? 8. Какие физические явления используют в навигации? РАЗДЕЛ 2 Геометрия земного сфероида
Размеры и форма Земли Земля представляет собой уникальное материальное тело, не имеющее аналогов в природе. Для удобства использования её поверхности и недр фигуру Земли представляют в виде некоторых известных геометрических тел (шар эллипсоид вращения, геоид, апиоид). В зависимости от формы определяются размеры Земли.
Исследования формы и размеров Земли имеют более чем двухтысячелетнюю историю. В трудах Аристотеля (384 – 322гг. до н.э.) имеется обзор доказательств шарообразности Земли, выполненных им и другими учеными, а также приведены ориентировочные размеры нашей планеты. Существенного уточнения размеров и формы Земли удалось достичь только в XIX веке, в основном, благодаря трудам Гаусса и Бесселя. Точные размеры основных параметров эллипсоида проводились в течение последних двух столетий. В зависимости от мест измерения получены различные эллипсоиды, имеющие следующие параметры Таблица 2.1 Параметры различных эллипсоидов
На основании современных исследований установлено, что Земля представляет собой геометрически неправильное (несимметричное) тело, трудно поддающееся математическому описанию. Одной из наиболее точных моделей Земли является геоид – уникальная геометрическая фигура, поверхность которой совпадает с невозмущенной поверхностью океана, продолженной под материками перпендикулярно отвесной линии. Форму геоида невозможно описать более или менее простыми аналитическими выражениями, поэтому в качестве модели Земли при решении многих практических и теоретических задач используется близкая к геоиду симметричная поверхность земной эллипсоид, который образуется путем вращения эллипса вокруг малой оси. Характеристиками эллипсоида являются параметры образующего его эллипса:
Из четырех названных величин обычно указываются только две, например, Земной эллипсоид обычно отождествляют с понятием земного сфероида, так как его полярное сжатие невелико, и он мало отличается от сферы. Параметры земного эллипсоида находятся на основе специально организованных многочисленных астрономо-геодезических и гравиметрических измерений на всей земной поверхности. Такие измерения проводятся в различных странах на протяжении последних трех столетий. В результате обработки измерений получен целый ряд моделей, каждая из которых с максимально возможной точно
стью описывает поверхность Земли в пределах определенного государства, материка или Земли в целом. Характеристики эллипсоида необходимы, прежде всего, для построения карт местности и привязки всех пунктов некоторой территории к единой геодезической системе координат. Эллипсоид, параметры которого официально приняты в какой-либо стране для построения геодезической системы координат, называется референц-эллипсоидом.
В ряде других стран при выполнении геодезических и картографических работ используются элементы земного эллипсоида Красовского, полученные в 1940г.: Во многих странах используются другие референц-эллипсоиды. Например, в Северной Америке принят эллипсоид Кларка 1866г. ( Ряд европейских стран в 80-е годы переходят на единую Европейскую систему координат, в которой используется референц-эллипсоид Хейфорда 1910г. ( Спутниковая навигационная система «Транзит» позволяет определять координаты объектов в «Мировой геодезической системе 1972 г.» (WGS – 72), рассчитанной на эллипсоиде с параметрами: Геодезические системы координат различаются не только размерами и формой референц- эллипсоидов, и взаимным расположением центров эллипсоидов, расстояние между которыми достигает почти километра. Несогласованность различных геодезических систем координат должна учитываться в судовождении при определениях места судна с помощью спутниковых или других радионавигационных систем, при использовании карт зарубежного издания, при переходах с карты на карту и в ряде других случаев. Координаты одних и тех же точек в разных геодезических системах нередко отличаются на несколько сот метров, а иногда – более чем на километр. При определениях места по спутниковым системам необходимо учитывать не только расхождения в координатных сетках, а и возвышение поверхности земного эллипсоида над поверхностью геоида, которое может достигать 100 м. И вызывать дополнительную погрешность в определении места судна до 200 м. и более. 2.2 Системы координат и направлений 2.2.1 Географические координаты
Для определения положения точки на поверхности Земного сфероида применяют географическую систему координат. В этой системе используют следующие понятия:
Северный полюс, это точка, откуда вращение Земли усматривается против часовой стрелки и обозначается РN. Южный полюс, это антипод северного полюса и обозначается РS. Такие географические полюса называют еще истинными. При пересечении сфероида плоскостями перпендикулярными оси Рисунок 2.1 – Координаты точки на Земле
вращения, на его поверхности образуются малые круги называемые параллелями. Если такая плоскость проходит через цент Земли, то ее след на поверхности сфероида образует большой круг называемый экватором. Следы от пересечения земного сфероида плоскостями, проходящими через ось вращения Земли, называют географическим меридианами или истинными меридианами. В соответствии с решением Международной меридианной конференции (Вашингтон 1884г.) в качестве нулевого (начального) установили меридиан, проходящий через Гринвическую обсерваторию (ее пассажный прибор) вблизи Лондона. Он получил название нулевого или гринвического меридиана. Меридиан, проходящий через точку наблюдения, называется истинным меридианом наблюдателя. Географической широтой (j) некоторой точки на поверхности земного сфероида называется угол между плоскостью экватора и нормалью к этой поверхности. Широта измеряется дугой меридиана от экватора до параллели точки. Плоскость экватора делит Землю на два полушария – северное и южное. Счет географических широт ведется от экватора к северу (N) или югу (S) от 0° до 90°. В алгеброических расчетах они имеют знаки (+) северная и (-) южная широта. Географической долготой (l) некоторой точки на поверхности сфероида называется двугранный угол между плоскостью начального (нулевого) меридиана и плоскостью меридиана данной точки. Плоскость нулевого (Гринвического) меридиана делит Землю на восточное и западное полушария. Долгота измеряется наименьшей дугой экватора от начального меридиана до меридиана точки. Пределы измерения долгот от 0° до 180°. Долгота имеет наименование и знак: восточная (+), если она измерялась к востоку от начального меридиана, и западная (-), если она измерялась к западу от начального меридиана.
повторяет дату прошедших суток. Если 180 меридиан пе  нормаль к поверхности совпадает с направлением на центр нормаль к поверхности совпадает с направлением на центр
Расчетная формула будет: РШ (Dj) = j2 - j1. Разность долгот (Dl) это наименьшая из дуг экватора, заключенная между меридианами точки отхода (l1) и точки прихода (l2). Пределы изменения разности долгот от 0° 180° и, если плавание осуществлялось в сторону востока (Е), то она имеет знак (+), если же в сторону запада (W), то у нее знак (-). Расчетная формула будет: РД (Dl) = l2 - l1. Формулы расчетов РШ и РД определяют не только их величины, но и наименование или знак (+; -). 2.2.2 Деление горизонта
Счет направлений в море относительно истинного меридиана является основополагающим. Предположим что наблюдатель находится в некоторой точке А
на поверхности Земли. Проведем мысленно плоскость (Н) перпендикулярную отвесной линии в данной точке. Это плоскость называется плоскостью истинного горизонта. Представим, что через точку А проходит другая, уже упоминавшаяся плоскость истинного меридиана (М). Эта плоскость называется плоскостью истинного меридиана наблюдателя (точка А) и в пересечении с плоскостью истинного горизонта образует линию истинного меридиана наблюдателя. Плоскость, проходящая через точку А перпендикулярно плоскости истинного меридиана называется плоскостью первого вертикала (V), в пересечении с плоскостью истинного горизонта образует линию перпендикулярную линии истинного меридиана. Линия истинного меридиана является полуденной линией и определяет направление на северный и южный полюса (N – S).
Рисунок 2.2 – Плоскости деления горизонта Линия, перпендикулярная линии истинного меридиана, дает направление E – W. Эти линии (N-S и E-W) в любой точке земной поверхности (кроме
полюсов) занимают строго определенное положение и служат для ориентирования. Направления N, S, E, W называются главными направлениями или главными румбами и делят плоскость истинного горизонта на четыре четверти (NO, SO, SW, NW). Направление, делящее каждую четверть пополам, называются четвертными румбами и имеют обозначение, соответствующее названию четверти (NO, SO, SW, NS). В зависимости от конкретных задач судовождения применяются следующие системы счета направлений: В круговой системе счета плоскость истинного горизонта делится на 360 градусов, причем за начало принято направление на север (норд истинный) и счет ведется от истинного меридиана по направлению движения часовой стрелки (от 0° до 360°). При этом направление на восток будет Е = 90°, на юг S = 180°, на запад W = 270° и на север N = 360° (0°). В полукруговой системе счет направлений ведут от главных румбов N или S в сторону востока Е или запада W от 0° до 180° (N 120 O; S 120 O; S 60 O; S 60 W). В четвертной системе счет направлений ведут от главных румбов N или S в каждой четверти от 0° до 90°, присваивая обозначение наименований четверти (NO 30; SO 30; SW 50; NW 50).
Вопросы для самопроверки 1. Какое значение для судовождения имеет форма и размеры земли? 2. Что такое референц-эллипсоиды и какие они бывают? 3. Какие широты точки на Земле используют в картографии? 4. Какие радиусы кривизны и длины дуг используют в судовождении? 5. Что такое геодезическая линия и какие методы её расчетов возможны?
6. Что такое локсодромия и её аналитическое описание? 7. Что такое ортодромия и соответствующие ей уравнения?
РАЗДЕЛ 3 Картографические проекции
Проекция в картографии понимается в более широком смысле, чем в геометрии. В картографии проекция рассматривается как способ переноса различных точек и линий с поверхности сфероида на плоскость. Такой перенос может осуществляться не только по нормалям к плоскости карты, как это принято в геометрии, а и по наклонным прямым, причем различные точки могут переноситься не параллельными между собой прямыми. Уравнение картографической проекции в общем случае записывается в виде х=ƒ1(φ, λ); у=ƒ2(φ, λ), где φ, λ – географические координаты точек на земной поверхности; х, у – картографические координаты на плоскости. Вместо прямоугольных координат х и у часто используются полярные координаты r и q. Функции ƒ1(φ, λ) и ƒ2(φ, λ) должны отвечать требованиям однозначности и непрерывности. Это значит, что каждому сочетанию j и l должна соответствовать только одна точка на карте и при непрерывном изменении j и l соответствующая точка на карте должна перемещаться также непрерывно. С помощью уравнений (40) рассчитывается и строится картографическая сетка меридианов и параллелей, относительно которой затем наносится на карту изображение определенного участка земной поверхности. Для построения картографической сетки задаются круглыми значениями j и l, например: через 20 и вычисляют соответствующие картографические координаты х и у точек пересечения меридианов и параллелей. Нанеся эти точки на бумагу, соединяют их плавными линиями и получают картографическую сетку. Каждая карта, в зависимости от используемой при ее построении картографической проекции, обладает определенными искажениями, и имеют характерный вид изображения меридианов параллелей. Поэтому картографические проекции классифицируются по характеру искажений и по виду изображения координатной сетки. По характеру искажений картографические проекции бывают: 1. Равноугольные (конформные) – передающие углы без искажений. В любой точке карты, построенной в этой проекции, эллипс искажений имеет равные полуоси, т. е. является окружностью. Масштаб такой карты изменяется при переходе от одной точки к другой, но в данной точке является постоянным во всех направлениях.
Морские навигационные карты строят в равноугольной проекции, масштаб которой изменяется только с широтой, оставаясь постоянным на данной параллели. 2. Равновеликие (эквивалентные) – сохраняющие постоянство масштаба площадей. Все площади на карте пропорциональны соответствующим площадям на земной сфероиде. 3. Равнопромежуточные – сохраняющие постоянство масштаба по одному из главных направлений, обычно – вдоль меридиана. 4. Производные – не обладающие свойствами равноугольности, равновеликости или равнопромежуточности, но имеющие другие существенные для решения определенных задач свойства. По виду изображения координатной сетки картографические проекции бывают: 1. Цилиндрические, при использовании которых меридианы и параллели на карте изображаются взаимно перпендикулярными прямыми. Уравнения цилиндрической проекции в общем случае имеют вид х = ƒ(φ); y = где ƒ(φ) – функция, определяющая характер искажений проекции и выражающая расстояние от экватора до параллели;
2. Азимутальные. На картах, построенных в азимутальной проекции, параллели изображаются концентрическими окружностями, а меридианы – радиальными прямыми, расходящимися из центра окружностей. Картографические координаты в этом случае являются полярными координатами ρ и θ, которые находятся по формулам: ρ = ƒ(φ); θ = λ. В зависимости от вида функции ƒ(φ) азимутальная проекция может быть равноугольной, равновеликой или равнопромежуточной или иметь любой другой
характер искажений. Например, один из видов азимутальной проекции – гномоническая – обладает важным свойством: любая дуга большого круга изображается в этой проекции прямой. 3. Конические. На картах, выполненных в таких проекциях, параллели – концентрические окружности, а меридианы – радиально расходящиеся прямые. Но, в отличие от азимутальных проекций, углы между меридианами здесь не равны разностям долгот, а лишь пропорциональны им: ρ = ƒ(φ); θ = Выбором функции ƒ(φ) можно задать любой необходимый характер искажений. Конические проекции часто используются при составлении карт погоды, которые передаются на суда с помощью факсимильной аппаратуры. Кроме перечисленных видов проекций существует еще множество других, которые относятся к произвольным, т.к. при решении задач судовождения они не используются.
Вопросы для самопроверки 1. Какие главные термины картографии должен знать судоводитель? 2. Что такое картографическая проекция и какие зависимости она определяет? 3. Что такое главные масштабы морской карты и как их применяют на практике? 4. Как разделяют картографические проекции по характеру искажений? 5. Какие виды картографических сеток используют в судовождении? 6. Какие бывают виды сеток стереографической проекции? 7. Как используется в судовождении меркаторская проекция?
РАЗДЕЛ 4 ТЕОРИЯ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА С ОЦЕНКОЙ ТОЧНОСТИ
4.1 Способы определения места судна (ОМС) 4.1.1 Сущность определения места судна
Во время перехода судоводитель постоянно должен знать местоположение судна, т.е. значение координат широты j и долготы l, эта задача решается ведением счисления и постоянным уточнением места обсервациями. Геометрические величины, получаемые из наблюдения внешних объектов для определения места судна, называют навигационными параметрами. Они подробно рассмотрены в первом разделе. Совокупность точек, в которых навигационный параметр сохраняет своё значение постоянным, называется изолинией U навигационного параметра. Изолиния навигационного параметра является функцией координат: U = f(j, l) = const. Для определения места судна необходимо получить, как минимум два навигационных параметра. Грамотное решение основной задачи судовождения – проводка судна по заданному маршруту – контролируется регулярными определениями места судна (ОМС). Теоретические основы и практическое выполнение этой работы изучают в математических основах судовождения (МОС). Сущность ОМС Для решения задачи необходимо и достаточно: - измерить и исправить значения не менее двух навигационных параметров; - найти изолинии соответствующие числовым значениям измеренных параметров; - определить координаты точки пересечения изолиний, учитывая возможную многозначность или неопределенность решения. Способы решения задачи ОМС Используя значения измеренных навигационных параметров задачу ОМС можно решить: - графически, проводя отрезки изолиний на карте в нужном месте; - аналитически, используя уравнения изолиний вручную или автоматически; - графо-аналитически, заменяя небольшие участки изолиний прямыми линиями, которые называются – линии положения (ЛП).
Применение результатов ОМС Полученную точку места судна используют для решения задач: - оценки точности места судна радиальной или эллиптической погрешностью; - сравнить соответствие полученных погрешностей места требованиям стандартов точности судовождения; - при необходимости определить способ ОМС удовлетворяющий стандартам и повторить решение задачи или наметить очередное время ОМС.
Основными методами определения места судна являются – метод изолиний и обобщённый метод линий положения (ЛП). Методом изолиний место судна можно определять, как графически, так и аналитически. При помощи графического способа, место судна определяется непосредственно на карте. Этот способ применяется, когда изолинии имеют простую форму, удобную для нанесения на карту. Графический способ подробно рассматривается в курсе навигации, посему, его рассматривать не будем. Аналитические способы дают место судна только путём математической обработки навигационных параметров. Математически, эти способы весьма сложны, но при современном развитии вычислительной техники, их использование значительно упрощается. Задачу определения места судна методом изолиний решают в следующем порядке: выполняются измерения навигационных параметров; составляются системы уравнений изолиний измеренных параметров;
подставляются в систему полученные параметры и система решается относительно jo и lo.
4.1.2 Изолинии и линии положения
Рисунок 4.1 – Изолинии глубины В обобщённом методе линий положения, навигационные параметры после некоторой математической обработки преобразовываются в унифицированные линии положения, основанные на использовании величины градиента g и его направления t, после чего графическим способом на карте или планшете определяется место судна. Если, изолиния показывает постоянное значение навигационного параметра, то градиент показывает направление и величину его изменения, разумеется, градиент всегда направлен перпендикулярно изолинии.
то есть показывает, как изменяется навигационный параметр с расстоянием. Один из простых, но показательных случаев, расчёт градиента глубин. Снимаем разность глубин, на рисунке – DU=10 метров, измеряем расстояние между изолиниями – D n=0,4 мили, направление градиента идёт по увеличению глубины. Получение формул для изолиний навигационных параметров, а так же для их градиентов приводятся в курсе лекций, а так же в [1], мы же ограничимся результатами этих выкладок, необходимыми для решения практических задач
Таблица 7. Характеристики навигационных параметров
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 723; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.9.149 (0.021 с.) |




 – полярное сжатие;
– полярное сжатие;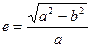 - эксцентриситет.
- эксцентриситет. , по которым можно определить остальные параметры эллипсоида.
, по которым можно определить остальные параметры эллипсоида. Земная ось, это воображаемая линия, вокруг которой происходит вращение Земли. Земная ось пронизывает сфероид в двух точках, называемых географическими полюсами.
Земная ось, это воображаемая линия, вокруг которой происходит вращение Земли. Земная ось пронизывает сфероид в двух точках, называемых географическими полюсами.

 , (4.1)
, (4.1)
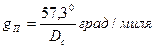
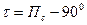


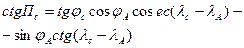
 град/миля
град/миля



