
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цилиндрическая равноугольная проекцияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее важными требованиями к навигационной карте являются необходимость передачи углов без искажений и изображения локсодромии в виде прямой. Этим двум требованиям отвечает только равноугольная цилиндрическая проекция, названная по имени ее создателя проекцией Меркатора. Найдем формулы для определения картографических координат х и y меркаторской проекции.
Рисунок 3.2 – Элементарные участки земного сфероида на Земле и морской карте
На рис. 3.2 показаны элементарный участок земного сфероида, ограниченный отрезкамимеридианов длиной Mdφ и отрезками параллелей длиной Ncosφdλ, и соответствующий участок карты со сторонами, равными dx и dy. Расстояние между меридианами в цилиндрической проекции пропорциональны λ, поэтому dy = Определим х = ƒ(φ) из условия равенства масштабов Масштабы вдоль меридиана и вдоль параллели, исходя из рис. 9 равны
Приравняв выражения для
Такой интеграл был уже найден при выводе уравнения локсодромии (см.п.3.4). Воспользовавшись этим решением, можно записать
или
Величина х, выражающая расстояние на карте от экватора до параллели с широтой φ, называется меридиональной частью и обозначается D. Коэффициент пропорциональности На реальной карте, масштаб которой отличается от 1, расстояния от экватора до заданных параллелей определяются умножением величины 3.5 Построение промыслово-навигационного планшета в меркаторской проекции.
Все промыслово-навигационные планшеты строят в меркарторской проекции; за главную параллель принимают среднюю параллель изображаемого района. При построении планшета может быть поставлена одна из двух задач: построить планшет в заданном масштабе данного района, границы которого определены приближенно; построить планшет определенного района, ограниченного заданными параллелями и меридианами, и вычислить масштаб данного планшета. Для того, что бы получить единые меры длинны для горизонтальной и вертикальной рамок карты, нам необходимо вычислять меридиональные части, выраженные в экваториальных милях. Длинна изображения одной экваториальной мили на меркарторской карте, выраженная в линейных мерах называется единицей карты. Единица карты зависит от масштаба карты, который может быть отнесён к любой параллели, носящей название главной параллели. Обозначив 1:Сэ главный масштаб по экватору, единицу карты можно рассчитать по следующей формуле:  , где , где
1:С0 – масштаб по главной параллели. Иначе единицу карты можно найти из следующей формулы:  , где , где
u – приведенная широта. 
Впрочем, если имеются картографические таблицы, то единицу карты можно рассчитать значительно проще, воспользовавшись т.4 или т.2. Если при построении планшета масштаб определяется тем условием, чтобы на него поместился заданный район, то единицу карты можно получить, разделив длину горизонтальной рамки карты на долготу, выраженную в минутах. Порядок решения. 1. Вычисляют единицу карты е. 2. Рассчитывают размеры рамки планшета: Горизонтальный размер b = e (l2 - l1), Вертикальный размер a = e DD, где DD – разность меридиональных частей между крайними параллелями, выбирается из т.26 МТ-63. 3. Наносят рамку планшета на лист бумаги. 4. Рассчитывают расстояния в миллиметрах промежуточных параллелей: yi = e (Di – DS) или yi = e (DN – Di). Эти вычисления удобно свести в таблицу вида:
5. Рассчитывают расстояния промежуточных меридианов от западной рамки планшета: xi = e (lW – li) или xi = e (li – lE) При условии, что расстояние между параллелями одинаково, достаточно его рассчитать один раз. 6. Наносят на планшет параллели и меридианы. Пример. Рассчитать рамку и картографическую сетку промыслово-навигационного планшета в масштабе С=100000.
Вопросы для самопроверки 1. Какие главные термины картографии должен знать судоводитель? 2. Что такое картографическая проекция и какие зависимости она определяет? 3. Что такое главные масштабы морской карты и как их применяют на практике? 4. Как разделяют картографические проекции по характеру искажений? 5. Какие виды картографических сеток используют в судовождении? 6. Какие бывают виды сеток стереографической проекции? 7. Как используется в судовождении меркаторская проекция?
РАЗДЕЛ 4 ТЕОРИЯ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА С ОЦЕНКОЙ ТОЧНОСТИ
4.1 Способы определения места судна (ОМС) 4.1.1 Сущность определения места судна
Во время перехода судоводитель постоянно должен знать местоположение судна, т.е. значение координат широты j и долготы l, эта задача решается ведением счисления и постоянным уточнением места обсервациями. Геометрические величины, получаемые из наблюдения внешних объектов для определения места судна, называют навигационными параметрами. Они подробно рассмотрены в первом разделе. Совокупность точек, в которых навигационный параметр сохраняет своё значение постоянным, называется изолинией U навигационного параметра. Изолиния навигационного параметра является функцией координат: U = f(j, l) = const. Для определения места судна необходимо получить, как минимум два навигационных параметра. Грамотное решение основной задачи судовождения – проводка судна по заданному маршруту – контролируется регулярными определениями места судна (ОМС). Теоретические основы и практическое выполнение этой работы изучают в математических основах судовождения (МОС). Сущность ОМС Для решения задачи необходимо и достаточно: - измерить и исправить значения не менее двух навигационных параметров; - найти изолинии соответствующие числовым значениям измеренных параметров; - определить координаты точки пересечения изолиний, учитывая возможную многозначность или неопределенность решения. Способы решения задачи ОМС Используя значения измеренных навигационных параметров задачу ОМС можно решить: - графически, проводя отрезки изолиний на карте в нужном месте; - аналитически, используя уравнения изолиний вручную или автоматически; - графо-аналитически, заменяя небольшие участки изолиний прямыми линиями, которые называются – линии положения (ЛП).
Применение результатов ОМС Полученную точку места судна используют для решения задач: - оценки точности места судна радиальной или эллиптической погрешностью; - сравнить соответствие полученных погрешностей места требованиям стандартов точности судовождения; - при необходимости определить способ ОМС удовлетворяющий стандартам и повторить решение задачи или наметить очередное время ОМС.
Основными методами определения места судна являются – метод изолиний и обобщённый метод линий положения (ЛП). Методом изолиний место судна можно определять, как графически, так и аналитически. При помощи графического способа, место судна определяется непосредственно на карте. Этот способ применяется, когда изолинии имеют простую форму, удобную для нанесения на карту. Графический способ подробно рассматривается в курсе навигации, посему, его рассматривать не будем. Аналитические способы дают место судна только путём математической обработки навигационных параметров. Математически, эти способы весьма сложны, но при современном развитии вычислительной техники, их использование значительно упрощается. Задачу определения места судна методом изолиний решают в следующем порядке: выполняются измерения навигационных параметров; составляются системы уравнений изолиний измеренных параметров;
подставляются в систему полученные параметры и система решается относительно jo и lo.
4.1.2 Изолинии и линии положения
Рисунок 4.1 – Изолинии глубины В обобщённом методе линий положения, навигационные параметры после некоторой математической обработки преобразовываются в унифицированные линии положения, основанные на использовании величины градиента g и его направления t, после чего графическим способом на карте или планшете определяется место судна. Если, изолиния показывает постоянное значение навигационного параметра, то градиент показывает направление и величину его изменения, разумеется, градиент всегда направлен перпендикулярно изолинии.
то есть показывает, как изменяется навигационный параметр с расстоянием. Один из простых, но показательных случаев, расчёт градиента глубин. Снимаем разность глубин, на рисунке – DU=10 метров, измеряем расстояние между изолиниями – D n=0,4 мили, направление градиента идёт по увеличению глубины. Получение формул для изолиний навигационных параметров, а так же для их градиентов приводятся в курсе лекций, а так же в [1], мы же ограничимся результатами этих выкладок, необходимыми для решения практических задач
Таблица 7. Характеристики навигационных параметров
jс – счислимая широта lс – счислимая долгота jА – широта измеряемого объекта lА – долгота измеряемого объекта DА, DВ – дистанция до измеряемого объекта Dc – счислимая дистанция d – расстояние между ориентирами Пс – счислимый пеленг g - сферическое схождение меридианов Для ортодромического пеленга с судна на ориентир
4.2 Графоаналитический метод
Он основан на обобщённом методе линий положения(ЛП). Суть способа состоит в том, что прямую, касательную к этой изолинии. Впервые этот метод был применён для определения места судна по на коротком отрезке, изолинию сколь угодно сложной формы можно заменить наблюдениям светил и проще его пояснить именно на этом примере. Предположим, что наблюдатель находится в точке М с координатами j и l, которые ему не известны и которые предстоит определить с достаточной точностью. В этой точке он измеряет высоту h светила С. Зная высоту светила можно провести круг равных высот с радиусом z = 90° - h. Разумеется, точка М будет находиться где-то на этой окружности.
Рисунок 4.2 – Высотная линия положения (ЛП)
Эту высоту наблюдатель измерил бы, если б находился в точке МС. Через эту точку так же можно провести круг равных высот с радиусом zС = 90° - hС. Разность n = h – hC даст нам расстояние в милях между действительным и счислимым кругами равных высот. Проведя азимут АС на светило и отложив на нём со своим знаком расстояние n, мы найдём определяющую точку К на действительном круге равных высот. Проведя через неё перпендикуляр, мы получим Высотную Линию Положения (ВЛП). Измерив высоту другого светила и произведя аналогичные расчёты, мы получим вторую ВЛП. Пересечение обоих ВЛП даст нам обсервованное место судна М0. Учитывая то, что радиус круга равных высот, как правило, на несколько порядков больше расстояния между точками МС и М, замена дуги на прямую линию практически не отразится на точности расчётов. То есть мы можем считать, что полученная нами точка М0 практически совпадёт с действительной точкой М. Переходя к обобщённому методу линий положения можно сказать, что навигационным параметром U, является истинная высота светила h, градиент g при этом равен единице, направление градиента совпадает с азимутом на светило. Обобщённый порядок расчётов при графоаналитическом способе выглядит следующим образом: 1. Измеряются навигационные параметры Uо1 и Uо2; 2. рассчитываются счислимые параметры Uс1 и Uс2 (по формулам приведенным в таблице),на моменты измерений Uо1 и Uо2; 3. вычисляются разности D U1 = Uо1 - Uс1; D U2 = Uо2 - Uс2; 4. рассчитываются модули g1 и g2 градиентов навигационных параметров и их направления t1 и t2; 5. по формулам
рассчитываются переносы; 6. на карте или планшете от счислимой точки по элементам t1, Dn1 и Dt2, n2 строятся линии положения I–I и II–II. Делается это следующим образом: Через счислимую точку при помощи транспортира проводится направление градиента t1 первого навигационного параметра. 1. Вдоль направления градиента откладывается перенос n1 по направлению, если перенос положителен, в противоположном – если отрицателен. 2. Через полученную точку жирным цветом проводится линия положения, обозначаемая с концов римской цифрой I. 3. Для построения второй линии положения производятся действия 1-3. 4. Пересечение высотных линий положения даёт нам обсервованную точку. 5. Снимаем координаты точки и невязку. 7. Производим оценку точности обсервованного места.
Следует учитывать, что производя построения на планшете, мы снимаем с него приращение координаты Dj, и отшествие Dw, далее при помощи углового масштаба, или формулы получаем приращение Dl. При аналитическом методе п.6, графических расчётов заменяется совместным решением системы уравнений:
 , где , где
Dw отшествие. Решив эту систему методом определителей и учитывая, что Dl=Dw/cos(jc), получим приращения координат:

где Q=t2-t1 далее определяем счислимые координаты: j0=jс+Dj l0=lс+Dl Как уже говорилось выше метод ЛП основывается на замене изолинии навигационного параметра, могущего иметь совершенно разные формы, на отрезок прямой, направленный по касательной к изолинии, естественно такая замена возможна лишь на небольших расстояниях, как правило, не превышающих 15-20 миль в приращениях координат. При получении приращений с большими значениями полученное место следует принять за первое приближение, а полученные координаты за счислимые и повторить рассчёты ещё раз.
4.3 Влияние случайных ошибок измерений на точность определяемого по двум ЛП места. 4.3.1 Смещение и вес ЛП.
Ошибки в измерениях навигационного параметра к ошибкам в изолиниях, а значит, и в ЛП, которые их заменяют. Навигационные параметры по которым строятся изолинии и ЛП, могут получаться совершенно разными способами и иметь величины ошибок имеющих разные размерности и величины, учитывая это для унификации удобно применять среднеквадратическое смещение ЛП равное
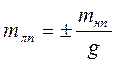 , где , где
mнп – СКП навигационного параметра, g – его градиент Она показывает, на сколько линейных единиц смещается ЛП при заданной величине СКП. Величину mнп называют смещением ЛП или полосой ЛП, т.к. при изменении абсолютного значения Uo, на величину ±mнп провести соответствующие этим значениям U'= Uo – mнп U''= Uo+ mнп границы, которые определят среднеквадратическую полосу положения. Вероятность попадания истинного значения в эту полосу определяется вероятностью погрешности навигационного параметра, для СКП ~ 0.67, для предельной СКП ~ 0.997, более подробно об этом говорилось ранее. Весом ЛП называют величину Pi обратно пропорциональную квадрату её смещения, которую рассчитывают по формуле Pi = 1/ m2 нп
При оценке точности рассматривается вероятность попадания истинного места судна в пределы фигуры ошибок, а не отклонения или ошибки от истинного
места судна. Теоретически необходимо рассматривать вероятность того, что фигура погрешности данной формы и площади данного размера, расположенная в данном месте накроет точку истинного места. Практически рассматривают отклонение, полагая центр фигуры вероятнейшим местом. На практике считают, чтобы погрешности измерения параметров распределены беспрерывно, т.е. мест судна бесконечно много. Для оценки точности места судна в судовождении применяют: эллипсы и круги погрешностей. 4.3.2 Эллипс погрешностей
При ОМС составляется и решается уравнение, прокладывается изолиния или ЛП отягощенная ошибками измерений. Величины и знаки истинных ошибок измерений носят случайный характер, и учесть их можно лишь статистически. Вывод формул оценки точности места базируется на предположениях: 1) Грубые ошибки или промахи, пропущенные при измерениях, исключены. 2) Компенсированы систематические ошибки измерений. 3) Ошибки вычислений и графики малы и несущественны. 4) Случайные ошибки измерения подчинены нормальному закону распространения случайных величин.
Рисунок 4.3 – Эллипс погрешностей места судна
Достоинства оценки места судна эллипсом: 1) Он имеет строго теоретическое обоснование. 2) Это единственная кривая, во всех точках которой плотность вероятности ошибки постоянна. 3) Вероятность попадания истинного места судна в область, ограниченную эллипсом, больше, чем у любой другой фигуры одинаковой с эллипсом площади. 4) Эллипс дает рассеяние мест судна по направлениям. При двух ЛП на практике, достаточно вписать приближенный эллипс в четырёхугольник, образованный полосами погрешностей. При этом вероятнейшим местом судна будет точка пересечения ЛП - центр эллипса погрешностей из-за того, что в элементарно малых окрестностях этой точки вероятность нахождения места судна больше, чем в аналогичных окрестностях любой другой точки.
Для строгого построения эллипса погрешностей рассматриваются векториальные ошибки Учитывая, что вектора

или
 ; ; 
Где a угол, определяющий направление большой полуоси эллипса, который всегда откладывается внутри острого угла Q от более точной ЛП. Ещё один способ расчета эллипса погрешностей по 2-м ЛП, заключается в использовании таблицы прил. № 5 к МТ-75 Аргументами для входа в таблицу служат величины
 Полуоси рассчитывают по формуле: Полуоси рассчитывают по формуле:
Таблица приложений S составлена по преобразованным формулам Аполлония.
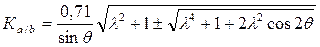 ; ; 
4.4 Графические методы отыскание вероятнейшего места судна при избыточном числе линий положения
При ОМС по двум ЛП или изолиниям имеет место существенный недостаток, а именно, практически отсутствует возможность проверить наличие систематических ошибок или промахов в измерениях и избавиться от их влияния. Частично эту проблему можно решить, получив избыточное число навигационных параметров, как правило, три или четыре. Получив три ЛП (изолинии) и нанеся их на карту, вследствие влияния случайных и систематических погрешностей, линии положения сойдуться не в одной точке, а мы получим треугольник погрешностей. К сожалению вычесление промахов, кроме очень крупных практически невозможно, но от воздействия одинаковых систематических ошибок избавиться возможно. Практически встают следующие вопросы: Каким образом лучше выбирать ориентиры? Где выбрать обсервованное место судна при равноточных и неравноточных измерениях? Как оценить точность полученного места и получить площадь, где находится место судна с наибольшей вероятностью.
4.4.1 Действие систематических ошибок
В теоретическом курсе показывается, что если между двумя ЛП положения провести биссектрису угла, то полученная «разностная» линия будет свободна от действия систематических ошибок. Для построения достаточно двух биссектрис. Эту операцию иногда называют «разгоном» треугольника погрешностей.
Для построения биссектрис именно тех углов, при вершинах треугольника перпендикулярно линиям положения, наносятся стрелочки в направлении азимута, затем проводится биссектриса меньшего угла между стрелочками (Рис. 4.4).
Другой способ разгона треугольника погрешностей заключается в смещении всех ЛП (или изолиний) на одну и ту же величину, в одном направлении. Далее сходные углы соединяются линиями. На пересечении этих линий мы получим место свободное от систематических погрешностей (рис.4.5).
Рисунок 4.5 – Получение биссектрис методом «разгона треугольника»
При построении биссектрис и определении обсервованного места может встретиться два случая: Ориентиры расположены в одной половине горизонта, в этом случае точка пересечения биссектрис будет лежать вне треугольника погрешностей (Рис.10 а). Вследствие того, что в реальных условиях на систематические ошибки накладываются ещё и случайные, приём может привести к грубым ошибкам в обсервованном месте, и его следует применять с большой осторожностью. Ориентиры расположены в разных частях горизонта. В этом случае точка пересечения биссектрис будет лежать внутри треугольника ошибок(Рис.10 б). Учитывая то, что внутри треугольника отклонение обсервованной точки от реальной значительно меньше, чем может быть снаружи, для обсервации рекомендуется подбирать ориентиры лежащие в разных частях горизонта. Следует помнить, что вышесказанное справедливо, лишь при допущении, что действие случайных ошибок равно нулю. Поэтому нельзя считать, что наши построения обнаруживают систематическую ошибку, скорее наоборот, они сами являются следствием предположения, что действуют только равные систематические ошибки. 4.4.2 Действие случайных ошибок
Случайные ошибки возникают из-за влияния разнородных факторов, учёт которых невозможен. В случае если все линии равноточные, а действие систематических ошибок равно нулю, вероятнейшее место будет находиться на пересечении антимедиан треугольника, которые представляет собой зеркальное изображение медиан относительно биссектрисы.
Рисунок 4.6 - Построение антимедиан
При увеличении треугольника в длину, обсервованное место смещается к более короткой стороне и прямому углу, что соответствует выводам из теории ошибок (чем ближе угол пересечения двух линий положения к 90°, тем вес этой точки больше). 4.4.3 Совместное действие систематических и случайных ошибок
В действительности систематические и случайные ошибки действуют всегда совместно. Исходя из этого, обе категории ошибок необходимо согласовывать так, что бы они не противоречили друг другу. Следовательно, для трёх линий положения самой выгодной разностью азимутов является 120°. Ориентиры для наблюдений не следует выбирать в одной половине горизонта, если же по ряду причин место выбрано именно таким образом, то метод биссектрис следует применять с большой осторожностью, желательно после анализа допущенных ошибок.
При выборе ориентиров в разных частях горизонта, вероятнейшее место всегда находится внутри треугольника погрешностей и, как правило, удобнее применять метод антимедиан.
4.4.4 Отыскание вероятнейшего места судна при неравноточных измерениях
В предыдущих параграфах, рассматривался случай обработки серии неравноточных измерений одного и того же навигационного параметра, зачастую приходится рассматривать случай обработки неравноточных измерений различных навигационных параметров, т.е. нескольких ЛП с различными СКП и соответственно весами p. Как уже говорилось ранее вес, это величина, характеризующая степень доверия к данному измерению или линии положения по сравнению с другими измерениями или линиями положения. Следовательно, в фигуре погрешностей состоящей из трёх или четырёх линий вероятнейшее место будет ближе к линии имеющей больший вес и к точкам пересечения линий, угол между которыми, ближе к 90°. Существует несколько, как графических, так и аналитических способов отыскания вероятнейшего места, при наличии трёх или более, неравноточных ЛП. Штурманский метод. Основан на том, что вероятнейшее место обладает важным свойством: при использовании n одновременных ЛП с весами P1, P2…Pn, выполняется следующее равенство:
d1, d2, d3 – перпендикуляры опущенные из вероятнейшего места Кв на соответствующие линии положения. Порядок действий:
1. Рассчитать абсолютные и относительные веса ЛП и обозначить относительные веса около каждой ЛП. 2. На глаз выбрать точку ближе к более тяжелым ЛП и углам более близким к 90°. 3. Провести из полученной точки перпендикуляры ко всем ЛП, измерить их длину и умножить каждую длину на соответствующий вес. 4. Построить по ним векторную сумму вида 5. Соединить начало и конец построения отрезком прямой, его середину принимают за новое место судна, если длинна полученного отрезка не более 0,5 мили, принимают полученную точку за вероятнейшее место, в противном случае построение повторяют до тех пор, пока отрезок не будет меньше 0,5 мили.
Рисунок 4.7 - Решение задачи штурманским методом
Центрографический метод Этот метод предполагает последовательное нахождение суммы весов точек пересечения 2-х ЛП и как результат, суммарный вес и вероятнейшее место судна. 1. Рассчитываем абсолютные веса ЛП, затем по формуле:
получаем относительные веса и округляем их до целого значения. 2. Получаем углы пересечения ЛП с меридианом bi = ti ± 90°. 3. Получаем углы пересечения ЛП друг с другом Qij, вычитая из большего значения bi меньшее bj. 4. Определяем веса точек пересечения ЛП Pij по формуле:
Вес точек пересечения линий положения с небольшим углом рассчитывать не имеет смысла за их малостью.
5. Последовательно получаем веса промежуточных точек, помня о том, что веса использованных точек заменяются совместным весом промежуточной. Например, на рис.8. вес
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.186.233 (0.011 с.) |

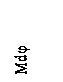


 dλ.
dλ. и
и  по главным направлениям.
по главным направлениям. ;
; 
 , откуда
, откуда  .
.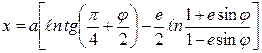

 a=
a=


 , (4.1)
, (4.1)
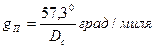
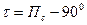


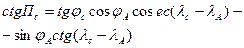
 град/миля
град/миля


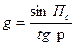 град/миля
град/миля


 миля
миля


 град/миля
град/миля





 В таблице:
В таблице: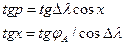
 При этом наблюдателю известны счислимые (приблизительные) координаты jС и lС точки. Из параллактического треугольника можно рассчитать счислимые высоту и азимут светила:
При этом наблюдателю известны счислимые (приблизительные) координаты jС и lС точки. Из параллактического треугольника можно рассчитать счислимые высоту и азимут светила:

 ;
; 
 ,
,
 , линии положения 1 и 2 по направлению ЛП2 и ЛП1.
, линии положения 1 и 2 по направлению ЛП2 и ЛП1. - сопряжённые полуоси эллипса используют теорему Аполлония
- сопряжённые полуоси эллипса используют теорему Аполлония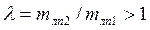

 Рисунок 4.4 – Биссектрисы внешних углов между ЛП
Рисунок 4.4 – Биссектрисы внешних углов между ЛП

 ,где (4.9)
,где (4.9)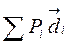 , для этого откладывается из нанесённой точки первый вектор, с длинной равной P1d1 и направлением первого перпендикуляра d1. Последующие вектора, откладываются из конца предыдущего.
, для этого откладывается из нанесённой точки первый вектор, с длинной равной P1d1 и направлением первого перпендикуляра d1. Последующие вектора, откладываются из конца предыдущего.





