
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вплив фазової структури полімерних композиційних матеріалів на його властивостіСодержание книги
Поиск на нашем сайте
Фазова структура композитів з дисперсними наповнювачами визначається трьома основними параметрами: вмістом наповнювача в ПКМ, розміром і формою частинок наповнювача, міжфазною взаємодією (властивостями МФШ).
Вміст наповнювача
Модуль пружності ПКМ. На рис. 8.3 крива 1 показує зміну відносного модуля ПКМ в інтервалі вмісту наповнювача φф від 0 до 100 %. При φф = 100 % модуль ПКМ дорівнює модулю наповнювача (другого полімеру): G = Gф. Модуль ПКМ при малому φф визначається властивостями матриці й помірно зростає з ростом φф. Модуль починає швидко зростати при φф = 20−30 %, коли відстані між частинками стають менше діаметра, що збільшує ймовірність їхнього безпосереднього контакту. При подальшому рості φф відбувається обернення фаз: другий компонент утворює другу безперервну фазу, а при φф > (70−80) % структура ПКМ відповідає оберненій дисперсії (частинки першого полімеру в матриці другого). Прогнозувати значення модуля пружності суміші полімерів шляхом розрахунку можна лише орієнтовно, оскільки змішання полімерів приводить до утворення несферичних часток одного полімеру в іншому при наявності широкого розподілу часток по розмірах. Крива 2 (рис 8.3) показує ріст модуля зі збільшенням вмісту недеформованих сферичних часток наповнювача в інтервалі φф = 0− φmax. Тут φmax відповідає граничному (максимально щільному) заповненню системи частками наповнювача. При φmax модуль прямує до величини модуля самого наповнювача. При введенні агрегованого наповнювача в полімер частина агрегатів руйнується залежно від умов змішання, тому значення φmax такого наповнювача зменшується порівняно з разрахованим φmax у матриці полімеру. Очевидно, що чим менший φmax, тим більш виражений ефект наповнення при тому самому значенні φ. Так, якщо ПКМ містить 15 % наповнювача при φmax = 60 %, те це малонаповнена система, але при тих же 15 % наповнення іншим наповнювачем, у якого φmax = 20 %, ПКМ є високонаповненим. Формули для розрахунку модуля ПКМ із матрицею, що деформується, і наповнювачем, що не деформується, повинні враховувати величину φmax. Наприклад, формула Муні має вигляд:
де kЕ – коефіцієнт Ейнштейна, рівний 2,5 для сферичних часток. Формула Муні придатна для розрахунку ПКМ із матрицею, що деформується, у якій коефіцієнт Пуассона νм = 0,5. Такою є, наприклад, епоксидна смола в області високоеластичності, що містить скляні сфери. Модуль ПКМ із матрицею, що мало деформується коли νм ≠ 0,5, можна розрахувати за рівнянням Корнера:
де G – модуль зсуву ПКМ; ν – коефіцієнт Пуассона; індекс «м» відноситься до матриці, індекс «ф» − до дисперсної фази. Такою є, наприклад, епоксидна смола, наповнена склосферами при Т < Тс. В’язкість ПКМ. В’язкість ПКМ часто залежить від вмісту наповнювача, подібно модулю. Якщо матриця ПКМ, що деформується, наповнена твердими частками, то при деформації зсуву або при малому розтягненні об’єм ПКМ не змінюється і νм = 0,5. Тоді
тобто зміну в’язкості можна розраховувати за тими ж формулам, що і зміну модуля. Якщо модуль матриці порівняльний з модулем наповнювача, що характерно для твердих матриць, то відносний модуль значно менший, ніж відносна в’язкість, і тоді справедливе рівняння, що враховує відхилення коефіцієнта Пуассона від 0,5.
В’язкість розплавів високонаповнених композитів може бути також розрахована за теорією вільного об’єму. Розрахунок заснований на певній аналогії структури суспензії й структури ПКМ при φ близькому до φmax. З рис. 8.3. видно, що при граничній упаковці (а) в суспензії є значний об’єм, незайнятий частинками. Він може перевищувати 30 %, але система буде не здатною до плину. Така ж особливість властива і засклованій рідині. Розсовування часток при розведенні або при нагріванні засклованої рідини(б) приводить до появи плинності. При цьому плинність (величина, зворотна в’язкості) тим більша, чим більша відстань між частками, тобто чим більше вільний об’єм:
де k – коефіцієнт консистенції; n – індекс плину; φвыльн = φmax – φ. Рівняння (8.9) справедливо для ПКМ із довільною формою часток і при їхньому широкому розподілі по розмірах. Як і у формулі Муні, для розрахунків по (8.9) необхідно знати φmax для даного наповнювача в даній матриці. Міцність ПКМ. При наявності досить міцного зв’язку на межі поділу матриця–наповнювач, коли матриця не є крихкою, міцність ПКМ збільшується з ростом φ. При збільшенні відносного ступеня наповнення до 0,2−0,3 перенапружені області навколо часток починають перекриватися, що полегшує розростання тріщин і міцність різко знижується. Міцність при стисненні, яка для твердих не наповнених полімерів приблизно у два рази більша за міцність при розтягненні, менш чутлива до наявності мікродефектів. Міцність при стисненні високонаповнених термореактивних смол помітно зменшується при φ → φmax, коли зв’язувального недостатньо для заповнення простору між частками й у ПКМ зростає поруватість. Міцність при розтягненні й стисненні знижується зі зменшенням міцності зв’язку на границі полімер–наповнювач і зі збільшенням розміру часток при постійному φ. Твердий наповнювач знижує міцність склоподібних полімерів. Термічний коефіцієнт розширення полімерів значно більший, ніж мінеральних наповнювачів, тому подальше охолодження засклованої матриці призводить навіть до її розтріскування поблизу часток наповнювача. Малі кількості наповнювача при φ ≤ 0,05 іноді забезпечують ріст міцності в кристалічних полімерах як за рахунок упорядкування розмірів кристалів, так і за рахунок уповільнення релаксаційних процесів, яке приводить до більш досконалої орієнтації молекул при деформації.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.007 с.) |


 ,
,

 ,
,


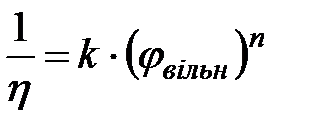 ,
,



