Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аномалія в’язкості за сталого плинуСодержание книги
Поиск на нашем сайте
Явище аномалії в’язкості полягає в тім, що ефективна в’язкість зі збільшенням τ і В умовах прояву аномалії в’язкості режими сталої зсувної плину описують функцією
У загальному випадку повна крива плину має S–подібний вигляд (рис. 3.5), охоплюючи граничні значення Всі теорії аномалії в’язкості в полімерних системах можна умовно розділити на наступні великі групи: - теорії, що зв’язують явище аномалії в’язкості із впливом напруження або швидкості зсуву на величину потенційного бар’єра, що перешкоджає переходу молекулярно-кінетичних одиниць із одного рівноважного стану в інший; - структурні теорії аномалії в’язкості, що розглядають залежність ефективної в’язкості від режиму плину як результат оборотного (тиксотропного) руйнування-відновлення надмолекулярної структури полімеру; - гідродинамічні теорії, у яких зменшення ефективної в’язкості полімерного матеріалу унаслідок підвищення швидкості зсуву пояснють зміною форми і, відповідно, опору переміщенню макромолекул. Однак, всі ці теорії описують аномалію в’язкості переважно з якісного боку. Відсутність теорії аномалії в’язкості, що добре погоджується з кількісними експериментальними даними, породила безліч емпіричних формул, найбільш важливою з яких є статечне рівняння виду:
де k − коефіцієнт консистенції; n − індекс плину. В інтервалі величин напружень і швидкостей зсуву, що мають найбільше значення в технології переробки полімерних матеріалів, рівняння (3.3) досить добре описує поведінку багатьох полімерних систем. Крім того, воно зручне з огляду простоту графічного визначення індексу плину і придатність для розрахунків підчас рішень різних прикладних задач. Величина початкової в’язкості має величезне значення для характеристики властивостей полімерних систем. Тому, у тих випадках, коли область практично постійної найбільшої в’язкості експериментально недосяжна, важливим стає метод її знаходження екстраполяцією залежності ln η = f(τ) до значення τ → 0. Помилка в цьому випадку не перевищує ± 10 %.
Аномалія в’язкості пов’язана з молекулярно-масовими характеристиками і особливостями хімічної будови полімерів. Припустимо, що кожен макромолекулярний ланцюг взаємодіє з іншими ланцюгами в певних вузлах − зачепленнях. Якщо одна з макромолекул починає рухатися, то вона тягне за собою всі макромолекули, пов’язані з нею взаємодіями різних порядків. Тому що вузли в просторовій сітці зачеплень не жорсткі, існує можливість міграції макромолекули відносно зачеплення. Тоді відставання в русі ланцюгів від первинного ланцюга буде тим більше, чим вище порядок зв’язку між ланцюгами. Якщо молекулярна маса полімеру М настільки мала, що вузли взаємодії зустрічаються в середньому рідше, ніж один на молекулу, то в’язкість повинна бути пропорційна молекулярній масі, тому що m ≈ M (m – довжина ділянки ланцюга між двома вузлами зачеплень). У випадку великої молекулярної маси (велика кількість зачеплень на кожну молекулу) η0 ≈ M5/2. У такий спосіб можна пояснити зміну характеру залежності в’язкості від молекулярної маси за деякого її критичного значення(Mкр), причому існування Mкр пов’язане з початком утворення вторинної структури (вузлів зачеплень) у полімері. Аномалія в’язкості проявляється в тому випадку, коли M > Mкр, тому що при цьому в полімері можливе винекненя надмолекулярних структур, які можна моделювати сіткою флуктуаційних зачеплень макромолекул. Цим самим аномалія в’язкості пов’язана зі зменшенням густини сітки зачеплень під впливом деформування полімеру. У разі збільшення молекулярної маси (M > Mкр) з ростом швидкостей і напружень зсуву зростає можливість руйнування сітки зачеплень і аномалія в’язкості стає усе більш значною. За деякого граничного значення M/Mкр ≈ 5 у полімері проявляється здатність переходити у високоеластичний стан, для якого характерно існування тривимірної сітки взаємозалежних макромолекул. Це є суто релаксаційний перехід, що здійснюється в ізотермічних умовах при Т > Тс. Він проявляється найбільш чітко в полімерах з вузьким молекулярно-масовим розподілом. У разі збільшення швидкості зсуву в ізотермічних умовах може спостерігатися перехід полімеру з текучого у високоеластичний стан. Це має місце, коли не встигають відбуватися множинні переміщення центрів тяжіння макромолекул за необоротної деформації. У цих умовах полімер поводиться як квазизшитий, у якому можуть накопичуватия значні оборотні (високоеластичні) деформації, а плинність подавлена. За M/Mкр > 10 перехід полімерів з плинного у високоеластичний стан виражений досить різко. У цьому випадку за швидкостей деформації, які перевищують критичні значення, плинність полімерів виявляється настільки подавленою, що реалізувати сталий ламінарний рух неможливо. Значення Mкр може змінюватися, залежно від природи полімерного ланцюга, в десятки разів. Отже, умови прояву аномалії в’язкості й переходу полімерів з плинного стану у високоеластичний визначає не абсолютне значення молекулярної маси, а відношення M/Mкр. Переходи з плинного стану у високоеластичний і навпаки визначає співвідношення швидкості деформації і часу релаксації. Добутком цих показників можна характеризувати в’язкопружні властивості полімеру:
Викладені теоретичні міркування можна проілюструвати схемою, що показує характер залежності об’ємної витрати Q від перепаду тиску ΔP підчас плину полімеру через циліндричний капіляр (рис. 3.7). Ділянка АВ відповідає ламінарному плину рідини, що подібна ньютонівській рідині на даній ділянці кривої плину. Починаючи від точки В, для якої τ/τкр ≈ 0,2, спостерігається коливальний режим нестійкго плину, що називається «еластичною турбулентністю» або «дробленням розплаву». Еластична турбулентність проявляється під впливом розвитку великих оборотних деформацій, які на режимах плину, що відповідають ділянці кривій ВСD, можуть досягати багатьох десятків відсотків. Ділянці плину СD відповідає помітна аномалія в’язкості, що виражена тим слабкіше, чим вужче молекулярно-масовий розподіл полімеру й вище температура плину. Точа D відповідає досягненню критичних значень швидкостей і напружень зсуву, за яких відбувається перехід полімеру у високоеластичний стан. Це супроводжується різким зниженням його плинності й зменшенням адгезії розплаву до стінки капіляра. У результаті спостерігається падіння опору руху полімеру в каналі й, відповідно, – стрибкоподібне підвищення витрати − ефект зриву потоку (вертикальна гілка DЕ). Унаслідок зриву потоку ламінарний плин полімеру перетворюється у ковзання відносно стінок каналу, тому в цьому режимі руху розрахунок швидкості зсуву стає неможливим. У результаті ковзання полімеру в каналі й супутнього йому падіння опору, перепад тиску, що відповідає критичному напруженню зсуву, зосереджується у вхідній зоні каналу, де різко зростає швидкість руху полімеру. Це призводить до розриву безперервності середовища як будь-якого пружньо–напруженого тіла (гілка ЕF). Хоча положення точки Е слабко залежить від молекулярної маси полімеру в межах даного гомологічного ряду, положення гілки АD значною мірою залежить від її, причому критична швидкість зсуву знижується приблизно на порядок у разі підвищення молекулярної маси у два рази. За значного зниження температури, аномалія в’язкості досить різко виражена в області високих напружень зсуву, що передують зриву потоку. Отже, за низьких температур навіть при незначному розширенні ММР перехід від ньютонівського плину до гілки зриву може бути плавним, а критична точка D неявно вираженою (крива СD). Уведення в полімер дисперсних наповнювачів спричиняє різке зростання в’язкості, але не змінює її температурного коефіцієнта. Отже, механізм плину наповнених полімерів майже не відрізняється від механізму плину ненаповнених полімерів, тобто підчас плину не відбувається розриву зв’язків між полімером і наповнювачем. Частки наповнювача є центрами суцільної просторової сітки, утворюваної в результаті орієнтації ланцюгів полімеру під впливом силового поля часток наповнювача (якщо наповнювач хімічно активний). Фіксування молекули полімеру на поверхні часток наповнювача передує утворенню навколо частки наповнювача оболонки з полімерних молекул, у яких полімер має підвищені механічні властивості. Для термопластичних полімерів також характерне утворення механічно міцної суцільної просторової структури. Такі структури мають тиксотропні властивості, причому для них характерна наявність тонких залишкових прошарків рідкого середовища в місцях контакту між частками. Ці прошарки, знижуючи міцність системи, забезпечують її здатність до помітних пластичних деформацій (пластичного плину) без значного руйнування структури, і до легкого її відновлення після повного або часткового руйнування. За цим передбачається, що у разі високих ступенів наповнення, внаслідок взаємодії самих часток наповнювача між собою, у системі можуть виникати ланцюжкові й сітчасті структури.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.231 (0.007 с.) |

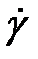 звичайно зменшується. Це явище має великий практичний інтерес, як основна характеристика гідродинамічної поведінки полімерних систем у реальних умовах підчас здійснення процесів переробки.
звичайно зменшується. Це явище має великий практичний інтерес, як основна характеристика гідродинамічної поведінки полімерних систем у реальних умовах підчас здійснення процесів переробки.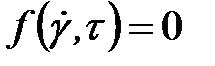 , графічне зображення якої називають «кривою плину».
, графічне зображення якої називають «кривою плину».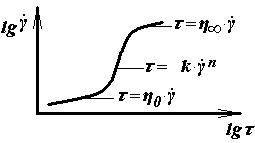
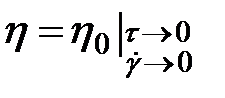 й
й 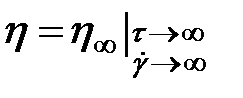 , що відповідає лінійним режимам ньютонівського плину. Для розплавів полімерів звичайно одержують тільки обмежену ділянку повної кривої. У вузькому інтервалі змінних криві плину можуть бути апроксимовані прямою (у подвійних логарифмічних координатах) з кутовим коефіцієнтом «n», що має назву індекс плину.
, що відповідає лінійним режимам ньютонівського плину. Для розплавів полімерів звичайно одержують тільки обмежену ділянку повної кривої. У вузькому інтервалі змінних криві плину можуть бути апроксимовані прямою (у подвійних логарифмічних координатах) з кутовим коефіцієнтом «n», що має назву індекс плину.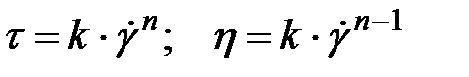

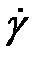 θ, де θ – час релаксації. Розглянутий вище перехід полімерів від одного фізичного стану в інше повинен відбуватися за певного значення
θ, де θ – час релаксації. Розглянутий вище перехід полімерів від одного фізичного стану в інше повинен відбуватися за певного значення 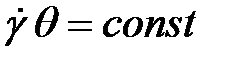 . Критична швидкість деформації
. Критична швидкість деформації 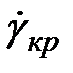 обернено пропорційна початкової в’язкості полімеру й, відповідно, залежить від температури. Але
обернено пропорційна початкової в’язкості полімеру й, відповідно, залежить від температури. Але 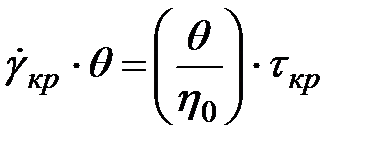 , де
, де 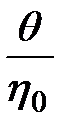 за М >> Mкр не повинне залежати від молекулярної маси й температури, тобто критичне напруження зсуву τкр має характерне значення для кожного полімергомологічного ряду, хоча воно порівняно слабко залежить від природи полімерного ланцюга, змінюючись у крайніх випадках приблизно у 10 разів. Для карбоцепних полімерів критичне напруження зсуву підвищується зі збільшенням кінетичної гнучкості макромолекул. Найбільш високим критичним напруженням зсуву відрізняються лінійні поліолефіни й полібутадієни (τкр = (3−4)×105 Па). Отже, неможливо реалізувати сталу ламінарну течію високомолекулярних полімерів за напружень зсуву, що перевершують наведені значення.
за М >> Mкр не повинне залежати від молекулярної маси й температури, тобто критичне напруження зсуву τкр має характерне значення для кожного полімергомологічного ряду, хоча воно порівняно слабко залежить від природи полімерного ланцюга, змінюючись у крайніх випадках приблизно у 10 разів. Для карбоцепних полімерів критичне напруження зсуву підвищується зі збільшенням кінетичної гнучкості макромолекул. Найбільш високим критичним напруженням зсуву відрізняються лінійні поліолефіни й полібутадієни (τкр = (3−4)×105 Па). Отже, неможливо реалізувати сталу ламінарну течію високомолекулярних полімерів за напружень зсуву, що перевершують наведені значення.