
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярні теорії розривної міцності полімерівСодержание книги
Поиск на нашем сайте
Міцність твердих тіл не є постійною величиною. У разі заданої схеми статичного руйнування (найчастіше – за постійного напруження) міцність визначає тривалість навантаження. Часова залежність міцності різних матеріалів за крихкого руйнування (з врахуванням температурного фактору) має назву рівняння Журкова:
де τ – довговічність зразка, тобто мінімальний час, що передує руйнуванню напруженого зразка; σ – напруження, постійне за величиною, що діє на зразок; u0 – енергія активації розриву зв’язку за напруженням, наближеним до 0; γ – структурна постійна, що залежить від ступеня орієнтації, технології переробки та ін.; k – константа Больцмана; τ0 – період теплових коливань атомів, що становить для полімерів 10−12−10−13 с; Τ − абсолютна температура; kT − міра енергії коливального руху атомів у молекулі. Рівняння (6.2) має досить суттєвий недолік. Для області малих напружень (σр → 0) довговічність виявляється скінченною величиною, що суперечить фізичному змісту, тому що суцільність ненавантаженого повинна бути постійною у часі. За одним з уточнень залежності (6.2) величина τ0 є функцією температури і напруження:
де а і γ –коефіцієнти, що залежать від концентрації напружень у вершині тріщини. З рівнянь (6.2) і (6.3) випливає наступне: - довговічність суттєво залежить від напруження й температури; - для розвитку процесу руйнування необхідна енергія активації, що зменшується за наявності напруження розтягу. Із цими результатами добре узгоджені молекулярні теорії розривної міцності полімерних матеріалів, які називають флуктуаційними теоріями міцності. Наприклад:
де Е − енергія, затрачувана на розрив зв’язку; n´ − число кістякових зв’язків у ланцюжках, що перетинають одиницю поперечного перерізу зразка і орієнтованих у напрямку дії сили; δ – приблизне значення деформації зразка перед розривом; ω − частота коливань зв’язку. Рівняння (6.4) добре узгоджене з експериментальними даними для аморфних склоподібних полімерів. Урахування тріщиноутворення дозволяє записати його у вигляді:
де σ0 – середнє напруження, що діє на один сегмент. Тривале статичне навантаження приводить до зміни положення молекулярного ланцюжка. Тому більші напруження в умовах тривалої експлуатації викликають переміщення ділянок ланцюгів, які перебудовуються убік зменшення напруження, що припадає на них. Число сегментів, що відчувають навантаження, або ефективних сегментів, згодом зменшується внаслідок релаксації коротких відрізків ланцюгів. Через це середнє напруження
де t – тривалість експерименту; Замінивши в (6.5) σ0 на σ із (6.6) і припустивши, що тривалість експерименту t без суттєвої помилки можна зрівняти з довговічністю τ, одержимо:
У цьому рівнянні часовий фактор урахований множником φ, що означає, що саме релаксаційний процес значною мірою визначає міцність полімерного матеріалу. Після перетворень (6.7) можна записати:
де Q – величина порядку одиниці; σ0 – середнє напруження, що діє на сегмент; коефіцієнт 4,2 біля σ0 враховує вплив тріщин і залежить від розмірів зразка. Часова залежність міцності для аморфних склоподібних полімерів має крутий характер – невелике збільшення напруження приводить до значної зміни довговічності. Однак, при навантаженні полімерів, деформація яких супроводжується значною високоеластичною деформацією, ця залежність набуває вид більш плавної степеневої функції. Припускають, що в еластиків структурна постійна γ залежить від орієнтаційного фактора, який разом з температурою входить у рівняння стану, що випливає з молекулярно-кінетичної природи високоеластичної деформації. Підставивши в рівняння (6.3) замість σ його значення σ = Тf(λ) одержимо:
де В (6.9) температурний фактор врахований експоненційним множником, але енергія активації є незалежною від прикладеного напруження. Для еластичних просторово зшитих полімерів
де b й В − постійні, залежні від природи полімеру.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.207 (0.009 с.) |


 ,
,  ,
,  ,
,
 ,
,
 , що припадає на один ефективний сегмент ланцюга, поступово зростає відповідно до виразу:
, що припадає на один ефективний сегмент ланцюга, поступово зростає відповідно до виразу: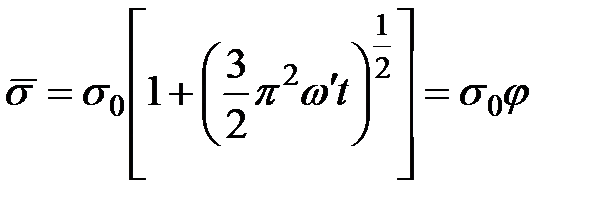
 – частота перескоків флуктуацій сегментів під дією напруження розтягу:
– частота перескоків флуктуацій сегментів під дією напруження розтягу:  ; а – константа, що дорівнює приблизно половині відстані, на яку зміщується сегмент при одному перескоку; ω0 – частота перескоків при відсутності зовнішньої сили.
; а – константа, що дорівнює приблизно половині відстані, на яку зміщується сегмент при одному перескоку; ω0 – частота перескоків при відсутності зовнішньої сили.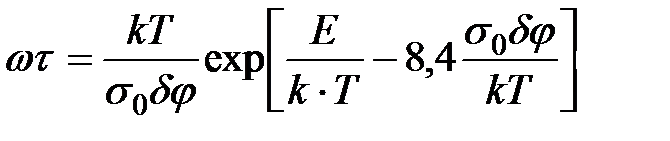 .
.
 ,
,

 ; с і n – безрозмірні постійні; Е∞ − рівноважний модуль; u − енергія активації.
; с і n – безрозмірні постійні; Е∞ − рівноважний модуль; u − енергія активації.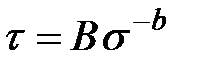 або
або 



