Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы получения количественных оценокСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Непосредственная количественная оценка используется как в случае, когда надо определить значение показателя, измеряемого количественно, так и в случае, когда надо оценить степень сравнительной предпочтительности различных объектов. В первом случае каждый из экспертов непосредственно указывает значение показателя для оцениваемого объекта. Это может быть конкретное числовое значение показателя для оцениваемого объекта. Например, стоимость жилой квартиры, цена единицы продукции, при которой она может иметь конкурентоспособный спрос, предполагаемая емкость рынка, оптимальный объем производства и т.д. Если эксперт затрудняется указать конкретное значение показателя, он может указать диапазон, в котором лежит значение оцениваемого показателя. Во втором случае, когда оценивается сравнительная предпочтительность объектов по тому или иному показателю, количественная оценка определяет степень их сравнительной предпочтительности. Например, большее значение оценки соответствует более предпочтительному альтернативному варианту. Иногда количественную оценку сравнительной предпочтительности объектов целесообразней производить в баллах, используя специальные балльные шкалы. 2. Метод средней точки используется, когда альтернативных вариантов достаточно много. Если через f(а1) обозначить оценку первого альтернативного варианта значения показателя, относительно которого определяется сравнительная предпочтительность объектов, через f(a2) – оценку второго альтернативного варианта, то далее эксперту предлагается подобрать третий альтернативный вариант, оценка которого f(a3) расположена в середине между значениями f(а1) и f(a2) и равна [f(а1) + f(a2)]:2. При этом в качестве первого и второго альтернативных вариантов целесообразно выбирать наименее и наиболее предпочтительные альтернативные варианты. Далее экспертом указывается альтернативный вариант а4, значение которого f(a4) расположено посередине между f(а1) и f(а3), и альтернативный вариант а5, значение которого f(а5) расположено между значениями f(а1) и f(а2). Процедура завершается, когда определяется сравнительная предпочтительность всех участвующих в экспертизе альтернативных вариантов. 3. Метод Черчмена – Акоффа используется при количественной оценке сравнительной предпочтительности альтернативных вариантов и допускает корректировку оценок, даваемых экспертами. Предполагается, что оценки альтернативных вариантов есть неотрицательные числа Все альтернативные варианты ранжируются по предпочтительности, и каждому из них эксперт присваивает количественные оценки в долях единицы. Далее эксперт сопоставляет по предпочтительности альтернативный вариант а1 и сумму остальных альтернативных вариантов. Если он предпочтительнее, то и значение Если Ц1 менее предпочтителен, чем сумма остальных альтернативных вариантов, то он сравнивается с суммой остальных альтернативных вариантов, за исключением последнего. Если альтернативный вариант Ц1 на каком-то шаге оказался предпочтительнее суммы остальных альтернативных вариантов и для оценок это соотношение подтверждается, то Ц1 из дальнейших рассмотрений исключается. Этот процесс продолжается до тех пор, пока последовательно не будут рассмотрены все альтернативные варианты. При практическом применении в случае большого числа сравниваемых вариантов в метод вносятся коррективы, снижающие его трудоемкость. Например, сразу может определяться сумма наибольшего числа альтернатив с отбрасыванием менее предпочтительных вариантов, которая меньше чем Подробный алгоритм метода рассмотрим далее, на примере. При оценивании объектов с помощью шкал можно рекомендовать метод Черчмена – Акоффа. Исходные положения оценки целей при использовании этого метода: - каждой цели - если цель - если - если - если - значимость общего результата - если общий результат Окончательное значение оценок Пример. В ходе анализа финансового состояния организации было выявлено, что уровень рентабельности недостаточно высок, доля собственных средств в активах не превышает 50% и показатели вероятности банкротства близки к критическим. Для преодоления сложившегося положения дирекция организации сформулировала следующие цели: - повысить долю собственных средств в активах; - повысить рентабельность; - снизить вероятность банкротства; - повысить квалификацию руководящих кадров; - ввести в ассортимент новый товар; - продать в течение года 2500 единиц товара; - создать региональное представительство в соседней области. Дирекция организации рассматривает три стратегии – А, В, С: А – расширение деятельности путем освоения новых видов продукции; В – расширение путем увеличения доли рынка по уже выпускаемой продукции; С – сохранение прежних позиций с увеличением относительной доли выпуска наиболее рентабельной продукции. Упорядочив результаты по степени их важности и присвоив им значения от 7 до 1:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.33 (0.009 с.) |

 . Если альтернативный вариант Ц1 предпочтительнее альтернативного варианта Ц2, то
. Если альтернативный вариант Ц1 предпочтительнее альтернативного варианта Ц2, то  больше, чем
больше, чем 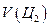 , а оценка одновременной реализации альтернативных вариантов Ц1 и Ц2 оценивается как
, а оценка одновременной реализации альтернативных вариантов Ц1 и Ц2 оценивается как 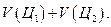
 соответствует действительное неотрицательное число
соответствует действительное неотрицательное число 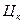 , то
, то  ;
;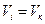 ;
; соответствуют целям
соответствуют целям 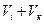 соответствует совокупности целей
соответствует совокупности целей  ;
;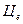 , то совместный результат
, то совместный результат