
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика поставщиков «Комбината хлебопродуктов»Содержание книги
Поиск на нашем сайте
Агрегированный коэффициент качества зерна рассчитывается по формуле:
где
Качество зерна определяется такими показателями, как натура, содержание клейковины и индекс деформации клейковины (ИДК). Их допустимые значения: - натура – 720-790 г/л; - клейковина – 21-32%; - ИДК – 40-90. За эталонные принимаются верхние допустимые значения клейковины, натуры и индекса деформации клейковины – ИДК (32%, 790 г/л и 60 соответственно), так как продукция, произведенная из сырья с такими характеристиками, пользуется наибольшим спросом. Действительные значения показателей. Курское зерно: - натура – 763 г/л; - клейковина – 23%; - ИДК – 91. Уральское зерно: - натура - 772 г/л; - клейковина – 28%; - ИДК – 68. Сибирское зерно: - натура - 781 г/л; - клейковина – 27%; - ИДК – 55. Возможные варианты оплаты сырья с точки зрения выгоды для организации (срока отвлечения средств из оборота, степени риска и т.д.) можно охарактеризовать следующим образом: - давальческая система – очень выгодно; - предоплата 100% - очень невыгодно; - по факту отгрузки – выгодно. Для количественной оценки удобства формы оплаты воспользуемся балльной шкалой Харрингтона: - очень невыгодно - 1; - невыгодно – 2; - средняя степень выгоды – 3; - выгодно – 4; - очень выгодно – 5. Надежность поставщиков оценим аналогично: - очень надежен – 1; - ненадежен – 2; - средне надежен – 3; - надежен – 4; - очень надежен – 5. Сопоставим полученные результаты с безразмерной шкалой. Диапазон изменения отвлеченных единиц зададим от 1 до 10. В качестве оптимальной примем наибольшую сумму безразмерных единиц. Для получения округленных значений по безразмерной шкале расширим диапазоны табличных значений (таблица 7.13). Таблица 7.13 Соответствие размерных и безразмерных характеристик
Теперь, вместо заданных характеристик подставим безразмерные величины, умножим их на соответствующие весовые коэффициенты, рассчитаем суммы этих произведений и найдем максимум (таблица 7.14). Таблица 7.14 Оценка альтернатив по сумме безразмерных величин При неравноценных критериях
Максимальная сумма произведений соответствует третьей альтернативе, т.е. при выборе альтернативы методом таблицы оценок оптимальным вариантом является закупка зерна у сибирского производителя. При применении метода «Полигон альтернатив» альтернативы представляют графически на полярной диаграмме (рисунок 7.1).
0,5
Свобода Прогресс Агроснабсервис Рисунок 7.1 Сравнение альтернатив выбора поставщика методом «Полигон альтернатив» Если наилучшее значение оценок альтернатив по всем критериям расположить дальше от центра окружности, оптимальным будет считаться вариант, которому соответствует многоугольник, очертивший наибольшую площадь. Рисунок 7.1 позволяет визуально оценить, что наибольшая площадь соответствует третьей альтернативе. Значения критериев соизмеримы, оси - промасштабированы, поэтому для ранжирования альтернатив можно рассчитать площади многоугольников. Угол между осями равен 450 (3600/8). Следовательно, площадь многоугольников определяется формулой:
где Результаты расчетов приведены в таблице 7.15. Таблица 7.15 Расчет площадей многоугольников для выбора Наилучшей альтернативы
Согласно данным таблицы 7.15 наибольшую площадь, занимает многоугольник, соответствующей третьей альтернативе (закупка зерна у ОАО «Агроснабсервис»). Результаты расчетов совпали с выводами, сделанными визуально и полученными по методу таблицы оценок. Начало
Метод анализа иерархий Вполне эффективным методом выбора на основе нескольких критериев является метод анализа иерархий (МАИ), разработанный Т. Саати. Этот метод оказывается полезным при принятии решений на основе как формализованных, так и неформализованных факторов. Суть МАИ – декомпозиция проблемы на части (элементы), которые оцениваются в шкале МАИ в виде суждений ЛПР (экспертов). А затем, после обработки совокупности суждений методом матричной алгебры, формируются в конечные оценки. При этом определяется относительная степень взаимного влияния в иерархии. Цель, факторы показательного оценивания и альтернативы образуют иерархическую структуру (рисунок 7.2).
Рисунок 7.2 Дерево целей МАИ:
Рассмотрение этой схемы (рисунок 7.2) позволяет сформулировать ряд положений, отражающих сущность метода анализа иерархий: 1. Число уровней иерархии, описывающих конкретную прикладную задачу, может быть различно и зависит от специфики задачи. Каждый элемент верхнего уровня является «направляющим» для элементов нижнего уровня. Это означает, что важность (весовой коэффициент факторов описываемой альтернативы) рассматривается относительно цели выбора альтернатив. Поэтому при бинарном сравнении факторов каждый из них оценивается относительно поставленной цели выбора и соответственно определяет уровни взаимного предпочтения. 2. Попарные сравнения факторов осуществляются в терминах доминирования одного из элементов над другим. Эти суждения в шкале МАИ выражаются в целых числах. Если элемент А доминирует над элементом В, то клетка квадратичной матрицы, соответствующей строке А и столбцу В, заполняется целым числом, а клетка, соответствующая строке В и столбцу А, заполняется обратным к нему числом. Если А и В эквивалентны, то в обе позиции записывается 1. 3. Для получения каждой матрицы требуется 4. При бинарном сравнении альтернатив, в особенности при близких оценках их показателей, возможны случаи нарушения требований транзитивности или других ошибок в суждениях, поэтому МАИ предусматривает специальный механизм определения согласованности оценок. Обработка результатов осуществляется на базе методов матричного анализа с использованием ряда специальных процедур оценки предпочтений ЛПР на основании шкалы МАИ (таблица 7.16).
Таблица 7.16 Шкала отношений МАИ
Для обоснования такой шкалы можно привести следующие аргументы. Замечено, что способность человека производить количественные разграничения хорошо представлено пятью определениями: равный, слабый, сильный, очень сильный, абсолютный. Можно принять компромиссные определения между отмеченными соседними, когда нужна большая точность. В целом требуется девять значений, выносимых при сравнении объектов суждений. Психологический предел – это 7 ±2 предметов при одновременном подтверждении, что если взять 7±2 отдельных предметов и если все они слегка отличаются друг от друга, то понадобится девять точек, чтобы различить их. Использование 1 (единицы) в начале шкалы соответствует отношению значимости объекта относительно самого себя и хорошо вписывается в формальную матричную процедуру МАИ (квадратных, обратно-симметричных матриц с положительными элементами). В МАИ рекомендованы четыре способа обработки данных. 1. Суммировать элементы каждой строки и нормализовать делением каждой суммы на суммы всех элементов. Сумма полученных результатов равна 1. Первый элемент результирующего вектора будет приоритетом первого объекта (в данном случае 1-го фактора) и т.д. 2. Суммировать элементы каждого столбца и получить обратные элементы этих сумм. Нормализовать их так, чтобы сумма равнялась 1, разделив каждую обратную величину на сумму всех обратных величин. 3. Разделить элементы каждого столбца на сумму элементов этого столбца, т.е. нормализовать столбец. Затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов в строке – усреднение по нормализованным столбцам. 4. Умножить В общем случае, когда матрица Определяется приближенная оценка главного собственного значения матрицы суждений. Для этого суммируется столбец суждений, а затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца – на вторую компоненту и т.д. Затем полученные числа суммируются. Таким образом получаем
При оценивании величины порога несогласованности суждений для матриц размером от 1 до 15 методом имитационного моделирования получены оценки случайного индекса (СИ). СИ является индексом согласованности для сгенерированной случайным образом (по шкале от 1 до 9) положительной обратно симметричной матрицы. В таблице 7.17) приведены средние (модельные) значения СИ для матриц порядка Таблица 7.17 Индексы согласованности
Продолжение таблицы 7.3
Отношение ИС к среднему СИ для матрицы суждений того же порядка Саати называет отношением согласованности (ОС):
где Значение Обобщенные веса (или приоритетность объекта при их выборе) определяются суммой произведений локальных приоритетов каждого объекта по каждому критерию на значимость этого критерия. Пример 7.4. Применим МАИ при выборе проекта для финансирования. В связи с недостатком финансовых средств в бюджете необходимо определить наиболее выгодный и жизненно необходимый для населения объект первоочередного финансирования. Выбранный объект должен удовлетворять первоочередные нужды города, при высокой степени рентабельности и минимальном риске проекта, для привлечения внешних и внутренних займов, покрывающих недостаток собственных средств бюджета. Стоимость проекта можно снизить с помощью использования собственных строительных материалов, производящихся в регионе. На экспертизу представлены следующие проекты. 1. Строительство жилья. 2. Строительство дорог (внутригородская структура). 3. Строительство и реконструкция жилищно-коммунальных инфраструктур (теплосеть, водоснабжение, газ). В условиях бюджетного дефицита одновременное финансирование всех трех проектов невозможно. В связи с этим необходимо определить первоочередность финансирования этих проектов. Группа экспертов выбрала следующие критерии для определения первоочередности финансирования: - стоимость проекта; - наличие внутреннего займа для проекта; - актуальность проекта для города; - срок эксплуатации проекта; - наличие внешних инвестиций для проекта; - риск вложения средств в проект; - отдача от проекта; - наличие собственных материалов для реализации проекта. В качестве основных критериев сравнения будет выступать стоимость проекта, а также актуальность проекта как для населения, так и для города в целом (она же будет характеризовать и уровень жизни населения в городе). Сроки эксплуатации проектов различны. Для жилья он составляет сроки около 50 лет, для дорого – 5, для жилищно-коммунальной системы – 20. Для изыскания дополнительных средств будем предполагать, что имеются как иностранные инвестиции, так и средства внутреннего займа, получаемые от выпуска ценных бумаг городскими службами. Первые будут в основном направлены на строительство дорог, а средства внутреннего займа – на строительство жилья. Наличие собственных строительных материалов позволяет экономить значительные средства; для строительства дорог и жилья материалы в регионе производятся, но для строительства коммунальной инфраструктуры их нет (пластиковые трубы, счетчики и т.д.). Такие ресурсы придется покупать в других регионах, т.е. данный проект представляется наиболее дорогим. И последнее, выбранный проект должен быстро окупиться и приносить прибыль. 1. Расчетная часть. Для начала представим нашу задачу в иерархической форме, определив цель, критерии выбора и альтернативы (рисунок 7.3), при этом обозначив варианты деятельности следующим образом: - строительство жилья – А; - строительство дорог – В; - строительство жилищно-коммунальных структур – С. 2. Важность критериев оценивается путем попарных сравнений каждого фактора с каждым другим. Для восьми элементов необходимо провести 28 попарных сравнений, определив, какой фактор и в какой мере превосходит другие (по 9-балльной шкале сравнений МАИ). Введем обозначения сравниваемых факторов: А1 – стоимость проекта; А2 – внутренний займ; А3 – потребность в проекте; А4 – срок эксплуатации; А5 – внешние инвестиции; А6 – риск проекта; А7 – отдача от проекта; А8 – имеются в наличии собственные строительные материалы.
Рисунок 7.3 – Дерево целей для выбора вида строительства
В таблице 7.18 представлены значения сравнений этих факторов. Таблица 7.18
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.012 с.) |

 ,
, - частные показатели качества зерна;
- частные показатели качества зерна; - эталонные значения показателей.
- эталонные значения показателей.
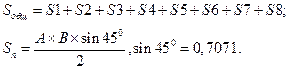
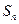 - площадь треугольника.
- площадь треугольника. = 1,7499
= 1,7499 



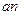
 ,
,  ,
,  - факторы (показатели), характеризующие альтернативы;
- факторы (показатели), характеризующие альтернативы;  суждений, где
суждений, где  - число факторов, если сравнение проводится среди них, или
- число факторов, если сравнение проводится среди них, или  при сравнении с
при сравнении с  присваивается одно из приведенных выше чисел, то действию
присваивается одно из приведенных выше чисел, то действию  содержит элементы согласованности суждений, указанные способы дают различные результаты векторов приоритетов. Расчет показателей согласованности выполняется следующим образом.
содержит элементы согласованности суждений, указанные способы дают различные результаты векторов приоритетов. Расчет показателей согласованности выполняется следующим образом. , которая называется оценкой максимума или главного значения матрицы
, которая называется оценкой максимума или главного значения матрицы  . Это приближение используется для оценки согласованности суждений эксперта. Чем ближе
. Это приближение используется для оценки согласованности суждений эксперта. Чем ближе 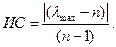

 при
при 
 считается приемлемым порогом допустимой согласованности суждений. Если значение
считается приемлемым порогом допустимой согласованности суждений. Если значение  , данные в матрице суждений необходимо уточнить.
, данные в матрице суждений необходимо уточнить.



