Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение оценок по методу Черчмена – АкоффаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассчитаем нормированные коэффициенты:
Проведем оценку стратегий по отношению к достижению каждой из семи целей:
Рассчитаем полезности стратегий: ПА = (0,8*7+0,7*6+0,6*5+0,4*4+1*3+0,8*2+0,7*1)/28=0.71=71%; ПВ = (0,8*7+0,7*6+0,7*5+0,5*4+0,4*3+0,9*2+0,8*1)/28= 0.68=68%; ПС = (0,8*7+0,8*6+0,8*5+0,6*4+0,3*3+0,7*2+0,6*1)/28=0,704=70.4%. Вывод: все три стратегии достаточно близки по полезности, однако для достижения указанных целей организации целесообразно выбрать стратегию А или стратегию С. 4. Метод лотерей (метод фон Неймана – Моргенштерна). Способ получения численных оценок альтернатив с помощью так называемых вероятностных смесей предложен фон Нейманом и Моргенштерном. В его основе лежит предположение, согласно которому эксперт для любой альтернативы Если указанная система предпочтений выполнена, то для каждой из набора основных альтернатив Таким образом, устанавливается существование функции полезности Методы получения качественных оценок 1. Экспертная классификация. Этот метод целесообразно использовать когда необходимо определить принадлежность оцениваемых альтернативных вариантов к установленным и принятым к использованию классам, уровням, сортам и т.д. Он может быть использован тогда, когда конкретные классы, к которым должны быть отнесены оцениваемые объекты, заранее не определены. Может быть заранее не определено и число классов, на которое производится разбиение оцениваемых объектов. Оно может быть установлено после завершения процедуры классификации. Если эксперту необходимо отнести каждый из альтернативных вариантов к одному из заранее установленных классов, то наиболее распространена процедура последовательного предъявления эксперту альтернативных вариантов. В соответствии с имеющейся у него информацией об оцениваемом объекте и используемой им оценочной системы эксперт определяет класс оцениваемого объекта. После завершения процедуры последовательного предъявления оцениваемых альтернативных вариантов эксперту может быть предъявлен результат его оценки в виде распределения вариантов по классам. Исходя из общего результата классификации эксперт может внести коррективы в собственные оценки. Если проводится коллективная экспертиза, то результаты классификации, указанные каждым экспертом, обрабатываются с целью получения результирующей коллективной экспертной оценки. 2. Метод парных сравнений является одним из наиболее распространенных методов оценки сравнительной предпочтительности альтернативных вариантов. При применении метода парных сравнений эксперту последовательно предлагаются пары альтернативных вариантов, для которых он должен указать более предпочтительный. Если эксперт относительно какой-либо пары объектов затрудняется это сделать, он вправе считать сравниваемые варианты равноценными либо несравнимыми. После анализа экспертом всех пар вариантов ведущим специалистом определяется их сравнительная предпочтительность по оценкам данного эксперта. В результате, если эксперт был последовательным в своих предпочтениях, все оцениваемые альтернативные варианты могут оказаться проранжированными по конкретному критерию, показателю, свойству. Если эксперт не признал некоторые варианты, будет достигнуто лишь их частичное упорядочение. В практике использования метода парных сравнений нередко приходится сталкиваться с непоследовательностью и даже противоречивостью оценок эксперта. В этих случаях проводят специальный анализ результатов экспертизы. При достаточно большом числе оцениваемых альтернативных вариантов процедура сравнения всех возможных пар становится для эксперта очень трудоемкой, возникает потребность в применении соответствующих модификаций метода парных сравнений. Примером такой модификации является метод анализа иерархий Т. Саати. 3. Множественные сравнения отличаются от парных тем, что экспертам последовательно предъявляются не пары, а тройки, четверки и более крупные группы альтернатив. Эксперт упорядочивает их по важности или разбивает на классы в зависимости от целей экспертизы. Множественные сравнения занимают промежуточное положение между парными сравнениями и ранжированиями. 4. Ранжирование альтернативных вариантов. Достаточно распространенной процедурой является также непосредственное ранжирование экспертом по предпочтительности оцениваемых альтернативных вариантов. В этом методе эксперту предъявляются отобранные для сравнительной альтернативные варианты (желательно не более 20-30) для их упорядочения по предпочтительности. Ранжирование сравниваемых объектов эксперт может осуществлять различными способами. Приведем два из них. В соответствии с первым эксперту предъявляется весь набор альтернативных вариантов и он указывает среди них наиболее предпочтительный. Затем эксперт указывает наиболее альтернативный вариант среди оставшихся и т.д., пока все оцениваемые альтернативные варианты не будут им проранжированы. При втором способе эксперту первоначально предъявляются два и больше альтернативных вариантов, которые надо упорядочить по предпочтениям. После первоначального ранжирования эксперту предлагаются новые, пока не оцененные альтернативные варианты. Он должен определить место вновь предъявленного альтернативного варианта среди проранжированных ранее. Процедура завершается после предъявления и оценки последнего альтернативного варианта. 5. Метод векторов предпочтений чаще всего используется для коллективного экспертного ранжирования. Эксперту предъявляется весь набор вариантов и предлагается для каждого из них указать, насколько он превосходит другие альтернативные варианты. Эта информация представляется в виде вектора; его первая компонента – число альтернативных вариантов, которые превосходят первый, вторая компонента – число альтернативных вариантов, которые превосходят второй и т.д. Если в векторе предпочтений каждое число встречается только один раз, это значит, что экспертом выполнено строгое ранжирование вариантов по предпочтениям. В противном случае полученный результат не является строгим ранжированием и отражает затруднения эксперта при оценке сравнительной предпочтительности отдельных альтернативных вариантов. Метод векторов предпочтений отличается сравнительно низкой трудоемкостью и может использоваться с учетом характера экспертизы. Этот метод может быть использован в тех случаях, когда у эксперта появляются трудности в использовании других методов оценки сравнительной предпочтительности альтернативных вариантов. 6. Гиперупорядочение. При гиперупорядочении предполагается рассмотрение разностей оценок альтернатив и их ранжирование. Эксперт сообщает информацию не только о ранжировании альтернатив, но и дополнительную информацию о соотношении их численных оценок. 7. Дискретные экспертные кривые. Если целью является разработка прогнозов или анализ динамики изменения показателей, характеризующих объект выработки и принятия управленческого решения, то целесообразно применять этот метод. Его идея такова. Определяется набор характерных точек, в которых наблюдается или ожидается смена тенденций изменения показателя, а также значения показателя в характерных точках. На участках между характерными точками предполагается, что значения показателя изменяются линейно, т.е. две соседние характерные точки кривой могут быть соединены отрезками прямой линии. Если есть достаточно веские основания для того чтобы определить нелинейные изменения значений показателя на участках кривой между характерными точками, имеет смысл от дискретных экспертных кривых перейти к экспертным кривым. При построении последних отрезки прямых линий могут быть заменены отрезками нелинейных кривых либо кривых, построенных непосредственно экспертами. К сожалению, в распоряжении экспертов не всегда имеется информация, позволяющая объективно судить о поведении кривой на участках между характерными точками. К тому же обработка результатов экспертных оценок и, в частности, определение результирующей коллективной экспертной оценки более объективны для дискретных экспертных кривых. Использование экспертных кривых позволяет наглядно представить различные сценарии развития ситуации, поэтому метод эффективен как при анализе ситуации принятия решения, так и непосредственно при выработке и принятии управленческих решений. Таким образом, чтобы система целей, сформированная организацией, была измеримой, необходим набор критериев, а для каждого критерия – соответствующая ему шкала определения степени достижения каждой цели. Только при наличии комплекса критериев, шкал и коэффициентов, позволяющих оценить сравнительную важность различных целей, а значит, и соответствующих им критериев, можно эффективно осуществлять процесс управления. Начало
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.130.96 (0.006 с.) |

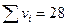 ;
;
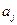 , менее предпочтительной, чем
, менее предпочтительной, чем  , но более предпочтительной, чем
, но более предпочтительной, чем 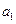 , может указать число
, может указать число 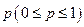 такое, что альтернатива
такое, что альтернатива 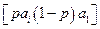 . Суть смешанной альтернативы в том, что альтернатива
. Суть смешанной альтернативы в том, что альтернатива 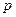 , а альтернатива
, а альтернатива 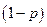 . Очевидно, что если
. Очевидно, что если 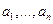 определяются числа
определяются числа 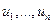 , характеризующие численную оценку смешанных альтернатив. Численная оценка смешанной альтернативы
, характеризующие численную оценку смешанных альтернатив. Численная оценка смешанной альтернативы 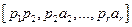 равна
равна 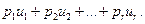 Смешанная альтернатива
Смешанная альтернатива  , если
, если