
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства и методы расчёта средних величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее часто используемая в экономико-статистической практике средняя арифметическая величина обладает рядом математических свойств, которые иногда упрощают её расчёт. Эти свойства следующие: 1. Если варианты уменьшить или увеличить на некоторое постоянное число, то средняя арифметическая величина соответственно уменьшится или увеличится на это число
2. Если варианты изменить в постоянное число раз столько же раз
3. Если частоты разделить или умножить на некоторое постоянное число, то средняя не изменится
4. Произведение средней арифметической на сумму частот равно сумме произведений вариантов на частоты
5. Алгебраическая сумма отклонения вариантов от средней величины равна нулю
Все перечисленные свойства следуют из определения средней арифметической взвешенной (см.раздел 4.2). Иногда расчёт средней арифметической величины удобно упростить, используя её математические свойства. Для этого нужно из всех вариант вычесть произвольную постоянную величину, полученную разность разделить на общий множитель, а затем исчисленную среднюю величину умножить на общий множитель и прибавить произвольную постоянную. В результате формула средней арифметической взвешенной получит следующий вид:
Средняя величина При выборе и расчёте вида средней величины необходимо учитывать наличие и характер исходных данных. Следует придерживаться следующего алгоритма. 1) Написать определяющее для расчёта среднего показателя соотношение, которое представляет собой суть связи между показателями задачи и определяет методологию расчёта обобщенного показателя. Например, если требуется определить среднюю месячную заработную плату работников, то таким соотношением является
где 2) Изучить исходные данные и установить наличие показателей в определяющем соотношении. В предложенном примере такими показателями являются
3) Подставить недостающие показатели в определяющее соотношение и установить вид средней. В нашем примере
т.е. в этом случае расчёт средней заработной платы можно выполнить по формуле средней гармонической взвешенной (см. раздел 4.2). Соотношения для определения средних структурных величин, представленные в разделе 4.2, предназначены для расчётов средних величин дискретных рядов. Методы расчёта средних по данным интервальных рядов имеют специфику, связанную с тем, что исследователь имеет дело не с дискретными значениями, а с интервалами группировочного признака. В этих случаях определения степенных средних сохраняются с учётом, что вместо значений вариант в них подставляются серединные значения интервалов. Для расчёта моды по данным интервального ряда используется следующая формула:
где
Для расчёта медианы в интервальном ряду используется следующая формула:
где
РЯДЫ РАСПРЕДЕЛЕНИЯ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ Ряды распределения
Результаты сводки и группировки данных статистического наблюдения оформляются в виде статистических рядов распределения и таблиц. Статистические ряды распределения – это упорядоченное расположение единиц изучаемой совокупности или групп по группировочному признаку. Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах её изменения, закономерностях наблюдаемого объекта. Ряды распределения, построенные по качественному признаку, называют атрибутивными. Например, распределение работников по занимаемой должности, профессии, образованию; распределение предприятий по форме собственности, виду основной деятельности и другим качественным признакам. При группировке ряда по количественному признаку образуются вариационные ряды. Вариационные ряды по способу построения бывают дискретными (прерывными), построенными на прерывной вариации признака (число человек в семье, касс в магазине, комнат в квартире), и интервальными (непрерывными), базирующимися на непрерывно изменяющемся значении признака, имеющем любые (в том числе и дробные) количественные выражения (объём товарооборота, величина фонда оплаты труда, выработка рабочего). При построении интервальных рядов распределения возникают вопросы о числе групп, величине интервала, его границах. Вариационные ряды состоят из двух элементов: варианты и частоты. Варианта – это отдельное значение варьируещего признака, которое он принимает в ряду распределения. Частотами называются численности отдельных вариант или численности единиц каждой группы вариационного ряда. Частоты, выраженные в долях единицы или в процентах к итогу называются частостями. Сумма частот составляет объём ряда распределения. Статистический ряд распределения по атрибутивному признаку представлен в табл.12.
Табл.12. Распределение продавцов магазина по категориям
Итого: 200 100
Если группировку в виде ряда распределения продавцов по категориям составить за два периода по данному магазину, то можно выявить происходящие структурные изменения (в данном случае – качественные сдвиги) в составе категории работников. Дискретные вариационные ряды распределения магазинов района по числу секций на две даты представлены в табл.13. В приведенных в табл.13 рядах частоты выражены в процентах, что позволяет посредством их сравнения обнаружить процесс увеличения количества товарных секций в магазинах на начало 2003г. по сравнению с началом 2000г. Это во многом связано со складывающейся конъюнктурой рынка, вызвавшей расширение ассортимента товаров и приведшей к разукрупнению существующих и созданию новых товарных секций.
Табл.13. Распределение магазинов района по числу товарных секций
Итого: 60 100 75 100
В статистических вариационных рядах существует определённая связь между частотами и значениями варьирующего признака: с увеличением признака величина частот вначале возрастает до определённой величины, а затем уменьшается. Такие изменения называют закономерностями распределения. Для характеристики закономерностей распределения вариационных рядов в статистике часто используют известные в математике законы распределения, примерами которых могут служить: - нормальное распределение
- распределение Пуассона
где В реальных статистических исследованиях социально-экономических процессов и явлений чаще всего закон распределения варьирующего признака в вариационных рядах неизвестен. В таких случаях для характеристики рядов распределений рассчитывают начальные и центральные моменты и связанные с ними показатели. Начальные моменты k-го порядка определяются по формулам
При Центральные моменты
При На практике чаще всего исчисляют следующие основные характеристики распределения:
которые достаточно точно выявляют форму распределения и весовое содержание варьирующего признака в нём. В математике доказывается теорема о том, что знание бесконечного числа моментов распределения эквивалентно полному знанию о распределении вариационного ряда.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 624; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.009 с.) |


 то средняя тоже изменится во
то средняя тоже изменится во




 где
где  .
. из значений вариант
из значений вариант  называется моментом первого порядка, а способ вычисления средней – способом моментов.
называется моментом первого порядка, а способ вычисления средней – способом моментов.
 – средняя заработная плата;
– средняя заработная плата;  – фонд заработной платы;
– фонд заработной платы;  численность работников.
численность работников. . Если какой-либо показатель отсутствует, то его необходимо определить по исходным данным, пользуясь определяющим соотношением. Например, при наличии данных о фондах заработной платы
. Если какой-либо показатель отсутствует, то его необходимо определить по исходным данным, пользуясь определяющим соотношением. Например, при наличии данных о фондах заработной платы 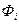 и средней заработной плате
и средней заработной плате  по группам работников, недостающие показатели находятся в виде
по группам работников, недостающие показатели находятся в виде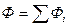
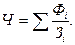
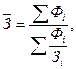
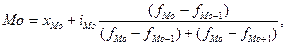
 - нижняя граница модального интервала;
- нижняя граница модального интервала; - размер модального интервала;
- размер модального интервала; - частота модального интервала;
- частота модального интервала; - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.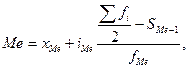
 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; - размер медианного интервала;
- размер медианного интервала; - сумма накопленных частот до медианного интервала;
- сумма накопленных частот до медианного интервала; - частота медианного интервала;
- частота медианного интервала; - полусумма частот ряда.
- полусумма частот ряда.

 - вероятность появления события с частотой
- вероятность появления события с частотой 
 - среднее число появления события в одинаковых независимых испытаниях;
- среднее число появления события в одинаковых независимых испытаниях; 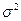 - дисперсия;
- дисперсия;  - вес или частота значения признака х.
- вес или частота значения признака х.
 имеем начальный момент
имеем начальный момент  - среднее значение признака; при
- среднее значение признака; при  имеем начальный момент второго порядка
имеем начальный момент второго порядка  - средний квадрат значений признака и т.д.
- средний квадрат значений признака и т.д. -го порядка определяют по формулам
-го порядка определяют по формулам
 - коэффициент асимметрии;
- коэффициент асимметрии; - эксцесс и др.,
- эксцесс и др.,


