
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексный метод в статистических исследованияхСодержание книги
Поиск на нашем сайте
Назначение и виды индексов
Особое значение в статистических исследованиях социально-экономических явлений имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых показателей во времени (индексы динамики), в пространстве (территориальные индексы), изучения структуры и взаимосвязей, выявления роли факторов в развитии сложных явлений. Индексами в статистике называют относительные показатели, характеризующие степень выполнения плана, изменения во времени, соотношение в пространстве уровней социально-экономических явлений, и представляющие собой отношение двух одноименных сопоставимых величин. Величина, которую сравнивают, называется отчётной или текущей, а величина, с которой сравнивают, называется базой индекса или базисной. По степени охвата изучаемого сложного явления различают индексы индивидуальные (элементарные) и общие (групповые). Индивидуальные индексы характеризуют изменение показателей отдельных единиц статистической совокупности (одного вида товара из совокупности ассортимента различных товаров, одного работника из совокупности работающих, одного предприятия из совокупности предприятий и т.д.). Индивидуальные индексы принято обозначать латинской буквой i и называть в зависимости от их экономического содержания, например: индивидуальный индекс физического объёма (количества) отдельного товара
где
где индивидуальный индекс себестоимости единицы отдельного вида продукции
где индивидуальный индекс производительности труда отдельного работника
где Представленные примеры индексов относятся к индексам динамики, поскольку они характеризуют развитие явления (физический объём, цена, себестоимость, производительность труда) во времени. Подстрочные индексы при показателях обычно обозначают: 1 – отчётный период; 2 – базисный период.
В знаменателе индекса может быть не только показатель базисного периода, но и показатели плана, нормы, другого территориального подразделения, например: индексы плана и нормы физического объёма
где территориальный индекс физического объёма отдельного товара
где Общие индексы характеризуют сводные результаты изменения явления по всем единицам, образующим статистическую совокупность (весь ассортимент различных товаров, совокупность рабочих, совокупность предприятий и т.д.). Сводные индексы обозначают латинской буквой общий индекс стоимости объёма продаж
где общий индекс себестоимости продукции
где индекс средней производительности труда
где В общих индексах суммирование производится по всем единицам рассматриваемой совокупности и только по тем показателям, которые могут непосредственно складываться. Если суммирование производится по группе единиц, являющихся частью совокупности, то получающиеся индексы иногда называют групповыми.
9.2. Способы образования индексов и связь между ними
Построение общих индексов может осуществляться в форме агрегатных или средних индексов. Основной формой общих индексов являются агрегатные индексы, в числителе и знаменателе которых содержатся соединенные наборы (агрегаты) элементов изучаемых совокупностей. Агрегатные индексы необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям с тем, чтобы получить сопоставимость разнородных единиц в сложных статистических совокупностях. При этом в числителе и знаменателе агрегатного индекса изменяется лишь значение индексируемой величины, а их соизмерители (множители) являются постоянными и фиксируются на одном уровне. Таким образом, на величине индекса сказывается лишь влияние фактора, который определяет изменение индексируемой величины.
Например, в агрегатной форме общий индекс цен с весами текущего периода (индекс Пааше)
в качестве индексируемых величин содержит цены отчётного (
При другом способе определения агрегатного индекса цен в качестве соизмерителя индексируемых величин
Разность числителя и знаменателя индекса Ласпейреса определяет абсолютный прирост в стоимостном объёме товаров базисного периода, если бы они продавались по ценам отчётного периода:
Индексы Пааше и Ласпейреса в общем случае различаются, поскольку характеризуют различные эффекты от изменения цен. Применение индексов Пааше и Ласпейреса зависит от цели исследования. Если исследование проводится для определения экономического эффекта отчётного периода от изменения цен в отчётном периоде по сравнению с базисным, то применяют индекс Пааше. Если же целью анализа является характеристика стоимостного объёма товаров такого же количества, что в базисном периоде, но по ценам текущего периода, то применяют индекс Ласпейреса. Иногда при образовании общего индекса цен вместо фактического количества товаров (
где В экономической статистике также широко применяются агрегатные индексы физического объёма товаров. Если в качестве индексируемых величин выступают количества товаров (
В случае, если в качестве соизмерителей привлекаются цены отчётного периода
Взаимосвязь общих индексов стоимостного объёма
Важной особенностью общих агрегатных и индивидуальных индексов является то, что они определяют не только относительное значение изменения изучаемого явления, но с их помощью можно найти абсолютные значения изменений. Если из числителя каждого индекса вычесть его знаменатель, то можно получить абсолютные приросты: общий прирост сопоставляемой величины и в том числе приросты за счёт отдельных факторов. Например, общий прирост стоимости товаров в отчётном периоде по сравнению с базисным
в том числе прирост стоимости за счёт изменения цен равен Иногда в статистике применяются общие индексы цен и физического объёма, предложенные американским экономистом И.Фишером. Индекс цен Фишера представляет собой среднюю геометрическую двух агрегатных индексов цен Пааше и Ласпейреса:
Соответствующая формула для определения индекса физического объёма имеет вид:
Индекс цен Фишера в силу относительной сложности расчёта и трудности экономической интерпретации на практике используется довольно редко. Чаще всего он применяется для исчисления индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объёма продукции, в которых происходят значительные изменения. Рассмотренная методика определения общих индексов цен в агрегатной форме аналогично применяется при построении индексов других качественных показателей: себестоимости
где Одной из форм выражения общих индексов являются средние индексы: средний арифметический взвешенный индекс и средний гармонический взвешенный индекс. Средний арифметический индекс строится таким образом, что он тождественен агрегатным индексам экстенсивных объёмных показателей. Так, например, агрегатный индекс физического объёма преобразуется в средний арифметический взвешенный индекс физического объёма (с учётом, что
Средний гармонический индекс является преобразованной формой агрегатных индексов качественных интенсивных показателей (цен, себестоимости единицы продукции, производительности труда работника и др.) Например, агрегатный индекс цен преобразуется в формулу гармонического взвешенного индекса цен (с учётом, что
Таким образом, средние индексы рассчитываются как средние величины индивидуальных индексов, причём средний арифметический индекс (например Выбор формы индекса в виде агрегатного или среднего зависит от характера исходных данных. Условием применения в экономической статистике агрегатных индексов является наличие данных о натуральных измерителях (соизмерителей) и их качественном содержании (например, количество и цена каждого вида товара). Если известны изменения индексируемого показателя и его веса по отдельным единицам совокупности, то пользуются формой средних индексов. При изучении динамики явлений за три и большее количество периодов индексы могут быть исчислены двумя путями: а) путём сопоставления показателей всех периодов поочерёдно с показателем одного периода, принятого за постоянную базу. Такие индексы с постоянным основанием называют базисными; б) путём сопоставления показателей каждого периода с величиной показателя непосредственно предшествующего периода. Такие индексы называют цепными. Базисные и цепные индексы связаны между собой следующими правилами: а) перемножив все цепные, получим последний базисный; б) разделив каждый последующий базисный на предыдущий базисный, получим цепной индекс.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.9.174 (0.008 с.) |



 - количества товара в отчётном и базисном периодах, соответственно;
- количества товара в отчётном и базисном периодах, соответственно;
 - цена товара в отчётном и базисном периодах, соответственно;
- цена товара в отчётном и базисном периодах, соответственно;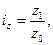
 - себестоимость продукции в отчётном и базисном периодах, соответственно;
- себестоимость продукции в отчётном и базисном периодах, соответственно;
 - производительность работника в отчётном и базисном периодах, соответственно.
- производительность работника в отчётном и базисном периодах, соответственно.

 - физический объём по плану и нормативный физический объём;
- физический объём по плану и нормативный физический объём;
 - физические объёмы товара, соответствующего территориям А и Б, соответственно (например, предприятиям А и Б, географическим районам А и Б и др.).
- физические объёмы товара, соответствующего территориям А и Б, соответственно (например, предприятиям А и Б, географическим районам А и Б и др.).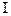 и их название соответствует показателям, изменение которых характеризуется, например:
и их название соответствует показателям, изменение которых характеризуется, например: 
 - индивидуальные значения стоимостных объёмов товара каждого вида в отчётном и базисном периодах, соответственно;
- индивидуальные значения стоимостных объёмов товара каждого вида в отчётном и базисном периодах, соответственно;
 - общая себестоимость продукции одного вида;
- общая себестоимость продукции одного вида;
 - средние значения производительности труда работника в отчётном и базисном периодах, соответственно,
- средние значения производительности труда работника в отчётном и базисном периодах, соответственно,  - численность работников в отчётном и базисном периодах, имеющих соответственно выработку
- численность работников в отчётном и базисном периодах, имеющих соответственно выработку  и
и  .
.
 ) и базисного (
) и базисного ( ) периодов, а в качестве соизмерителей (весов) используются данные о количестве разнородных товаров (
) периодов, а в качестве соизмерителей (весов) используются данные о количестве разнородных товаров ( ) в текущем периоде. В числителе индекса при суммировании по всей совокупности товаров образуется сумма стоимости товаров в текущем периоде по ценам того же периода (
) в текущем периоде. В числителе индекса при суммировании по всей совокупности товаров образуется сумма стоимости товаров в текущем периоде по ценам того же периода ( ), а в знаменателе – значение стоимости товаров в текущем периоде по ценам базисного периода (
), а в знаменателе – значение стоимости товаров в текущем периоде по ценам базисного периода ( ). В данном случае индекс Пааше характеризует динамику (изменение) общего уровня цен по рассматриваемому ассортименту товаров вследствие влияния на изменение цен фактора времени. Разность числителя и знаменателя индекса определяет абсолютный прирост стоимостного объёма товаров в текущем периоде, за счёт фактора изменения цен в текущем периоде по сравнению с базисным периодом:
). В данном случае индекс Пааше характеризует динамику (изменение) общего уровня цен по рассматриваемому ассортименту товаров вследствие влияния на изменение цен фактора времени. Разность числителя и знаменателя индекса определяет абсолютный прирост стоимостного объёма товаров в текущем периоде, за счёт фактора изменения цен в текущем периоде по сравнению с базисным периодом:
 . Агрегатная форма такого общего индекса цен с весами базисного периода (индекс Ласпейреса) имеет вид:
. Агрегатная форма такого общего индекса цен с весами базисного периода (индекс Ласпейреса) имеет вид:
 .
. и
и  . При таком способе образования формула общего индекса имеет вид
. При таком способе образования формула общего индекса имеет вид
 то общий индекс физического объёма имеет вид
то общий индекс физического объёма имеет вид
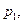 то общий индекс физического объёма имеет вид
то общий индекс физического объёма имеет вид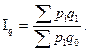
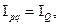 цен
цен 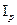 и физического объёма
и физического объёма  всегда обусловлена фундаментальной связью стоимости, цены и количества (
всегда обусловлена фундаментальной связью стоимости, цены и количества ( ) и может быть представлена выражением
) и может быть представлена выражением

 равен
равен
 и за счёт изменения физического объёма товаров равен
и за счёт изменения физического объёма товаров равен 


 производительности труда
производительности труда  и др. Примеры взаимосвязей общих индексов:
и др. Примеры взаимосвязей общих индексов:

 - общие индексы объёма продукции и объёма себестоимости продукции, соответственно;
- общие индексы объёма продукции и объёма себестоимости продукции, соответственно;  - общие индексы производительности труда и себестоимости единицы продукции, соответственно;
- общие индексы производительности труда и себестоимости единицы продукции, соответственно;  - общие индексы численности работников и физического объёма продукции, соответственно.
- общие индексы численности работников и физического объёма продукции, соответственно.



 ):
):
 ) исчисляется с весами по стоимостному объёму базисного периода (
) исчисляется с весами по стоимостному объёму базисного периода ( ), а средний гармонический индекс (например
), а средний гармонический индекс (например  ) исчисляется с весами по стоимостному объёму отчётного периода (
) исчисляется с весами по стоимостному объёму отчётного периода ( ).
).


