
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Н = –284,2–3×8,314×10–3×298 = –284,2–7,4 = –291,6 кДж/моль (R = 8,314 Дж/(моль×К).Содержание книги
Поиск на нашем сайте
δQ = dU+δW = dU+pdV+δW′, (1.7) де: pdV – елементарна робота, виконана системою як протидія зовнішньому тиску (робота розширення); δW′ – сума всіх видів елементарних робіт (магнітна, електрична та ін.). Величину δW′ називають корисною роботою. У хімічній термодинаміці береться до уваги тільки робота розширення, а роботу δW′ вважають рівною нулю. Тому: δW = pdV. (1.8) Звідки: δQ = dU+pdV. (1.9)
§3. Теплові ефекти. Закон Гесса. Теплоємність. Розділ хімічної термодинаміки, що вивчає теплові ефекти хімічних реакцій, називають термохімією. При ізотермічному процесі передача теплоти від одного тіла до другого відбувається за сталої температури. Якщо газ ідеальний, то внутрішня енергія 1 моля газу не залежить ні від об’єму, який займає газ, ні від тиску, а залежить лише від температури. Отже, в ізотермічному процесі, коли U = const, рівняння (1.9) буде мати вигляд: δQT = δW = pdV. (1.10) Після інтегрування вираз (1.10) перетворюється на: QT = W = pdV. (1.11) Це означає, що при ізотермічному процесі теплота повністю перетворюється на роботу розширення. Для 1 моля газу
При ізохорному процесі об’єм системи постійний. При dV = 0 елементарна робота розширення системи dW = pdV = 0. У цих умовах рівняння (1.9) має вигляд: δQv = dU, (1.13)
Отже, при V=const вся кількість теплоти, що підведена до системи, використовується на збільшення її внутрішньої енергії. Рівняння (1.14) показує, що Qv є функцією стану. Для реакції у конденсованій фазі ΔV ≈ 0; Qp = Qv. Незважаючи на рівність Qp і Qv, розрахунки теплових ефектів реакцій у конденсованих системах проводять в основному при p = const. У ізобарному процесі p = const. Рівняння (1.9) видозміниться таким чином: δQp = dU+d(pV) = d(U+pV) = dH, (1.15)
Кількість теплоти ізобарного процесу є мірою зміни ентальпії. Оскільки H = U+pV є функцією стану, то і Qp набуває властивості функції стану. Звичайно хімічні реакції проводять при постійному об’ємі або постійному тиску. Згідно з (1.14): QV = ΔU, (1.17) а при постійному тиску, виходячи із (1.16) і (1.2), Qp = ΔU+pΔV = ΔH. (1.18) Рівняння (1.17) і (1.18) справедливі лише за умови, що об’єм і тиск не змінюються від початку до кінця реакції. Кількість теплоти QV і Qp у (1.17) і (1.18) часто називають ізохорним та ізобарним тепловим ефектом реакцій. Тепловим ефектом хімічної реакції називають максимальну кількість теплоти, яка виділяється або поглинається у незворотному процесі при постійному об’ємі або тиску і за умови, що продукти реакції та вихідні речовини мають однакову температуру і відсутні інші види робіт, крім розширення. Оскільки у рівняннях (1.17) і (1.18) теплові ефекти QV і Qp є функціями стану, то звідси випливає термодинамічне обґрунтування закону, відкритого експериментально Г.Гессом: тепловий ефект хімічного процесу не залежить від способу перебігу його, а залежить від початкового і кінцевого станів реагуючих речовин. Закон Гесса – це окремий випадок першого закону термодинаміки відносно інших процесів, що відбуваються в ізохорних або ізобарних умовах. Наприклад, процес горіння вуглецю можна здійснити у дві стадії: спочатку добути карбон (ІІ) оксид: С(к)+1/2О2(г) = CО(г); ΔН1 = –124,3 кДж/моль, потім його окиснити в карбон (ІV) оксид: СO(г)+1/2О2(г) = CО2(г); ΔН2 = –284,9 кДж/моль. Сумарний тепловий ефект ΔН1+ΔН2 = –409,2 кДж/моль. Перехід від вихідних речовин до кінцевих можна здійснити і в одну стадію: С(к)+О2(г) = СО2(г); ΔН3 = –409,2 кДж/моль. Закон Гесса стверджує, що ці теплові ефекти пов’язані між собою співвідношенням: ΔН3 = ΔН1+ΔН2, тобто незалежно від шляху одержання продуктів сумарний тепловий ефект для всіх шляхів буде однаковим. Закон Гесса є основним законом термохімії. Із рівняння (1.17) і (1.18) випливає, що: Qp–QV = pΔV. (1.19) Різниця теплових ефектів при сталому тиску і об’ємі дорівнює роботі розширення. Згідно з рівнянням стану ідеальних газів Клапейрона-Менделєєва, pV = νRT, звідки: pΔV = ΔνRT, (1.20) де: Δν – зміна числа молів газоподібних учасників реакції. Якщо це значення ввести у (1.19), то одержуємо рівняння, що виражає співвідношення між ізобарним та ізохорним тепловими ефектами: Qp–QV = ΔνRT або, згідно з (1.16) і (1.17), ΔН = ΔU+ΔνRT. (1.21) Якщо Δν = 0, то ΔH = ΔU. При наявності у реакції твердих і рідких компонентів при обчисленні Δν вони до уваги не беруться. При перебігу хімічних реакцій зміна числа молів (Δν) дорівнює різниці стехіометричних коефіцієнтів (Δn) у рівнянні, тому Δν = Δn. Приклад. Визначити тепловий ефект реакції утворення води. 2H2(г)+О2(г) = 2Н2О(p) при сталому тиску і температурі 298 К, якщо тепловий ефект за постійним об’ємом дорівнює –284,2 кДж/моль. Розв’язування. Δn = Σnпрод–Σnвихідн = 0–3 = –3. Згідно з (1.21) Тепловий ефект є позитивним (ΔH>0), якщо Hкінц>Hпочатк, тобто коли теплота поглинається (ендотермічна реакція). Якщо Hкінц<Hпочатк, то ΔH<0, тобто теплота виділяється (екзотермічна реакція). Для порівняння теплових ефектів різних реакцій і проведення термохімічних розрахунків введено поняття теплового ефекту за стандартних умов. Тепловим ефектом за стандартних умов (ΔHr) називають такий тепловий ефект, який супроводжує реакцію при стандартному тиску p0 = 1,013×105 Па і температурі Т К. Як базисну вибирають температуру 298 К. Тепловий ефект при стандартних умовах розраховують за стандартними теплотами утворення і згоряння. Стандартною теплотою утворення називають тепловий ефект реакції утворення 1 моля даної речовини із простих речовин (або елементів) при тиску 1,013×105 Па і за умови, що всі компоненти реакції є у стійких агрегатних станах. Для зручності порівняння стандартних теплот утворення їх прирівнюють до базисної температури 298 К. Стандартні теплоти утворення позначають Так само як і стандартні теплоти утворення, стандартні теплоти згоряння відносять до базисної температури 298 K. Продуктами згоряння у цих умовах є СО2(г), Н2О(р), SO2 (г), N2(г) і т.д. Стандартні теплоти згоряння простих оксидів у стійких станах прийняті за нуль. Теплоти згоряння позначають Користуючись табличними даними
Таблиця 1.1. Значення стандартних теплот утворення і згоряння, середні теплоємності для деяких речовин у газуватому стані. Молекулярна формула
кДж/моль
кДж/моль С Дж/(моль K) HJ 26,04 – 17,5 CH4 –74,85 802,32 – CO2 –393,51 – – CO –110,50 283,00 – NH3 –46,19 – 35,68 H2 241,84 28,84 H2O –242,76 – C6H6 83,76 3298,4 – Cl2 – 36,70 CHCl3 100,40 – 81,40 HCl 92,30 – 26,50 H2S –2,15 – 33,97
При розрахунках теплових ефектів використовують наслідки закону Гесса. 1. Тепловий ефект реакції за стандартних умовах дорівнює різниці між сумою теплот утворення продуктів реакції і сумою теплот утворення вихідних речовин, помножених на відповідні стехіометричні коефіцієнти: ΔHr298 = Σni Приклад. Визначити теплоту утворення HJ(г) за реакцією: ½H2(г)+½J2(г) = HJ(г), ΔHr298 = ? Розв’язування. Тепловий ефект цієї реакції ∆Нr298, згідно з (1.22), є теплота утворення HJ(г), тому що ΔHr298 = 2. Тепловий ефект реакції за стандартних умов дорівнює різниці між сумою теплот згоряння вихідних речовин і сумою теплот згоряння продуктів реакції, помножених на відповідні стехіометричні коефіцієнти: ΔHr298 = Σni Приклад. Розрахувати стандартний тепловий ефект реакції СН4(г)+СО2(г) = 2СО(г)+2Н2(г) за стандартними теплотами згоряння. Розв’язування. Згідно з (1.23), ΔHr298 = Із таблиці 1.1 знаходимо стандартні теплоти згоряння (кДж/моль): для СН4 –802,32; СО2 0; СO –283,0; Н2 –241,84. ∆Нr298 = –802,32–(–2´283,0)+(–2´241,84) = +247,36 кДЖ/моль (реакція ендотермічна). Важливою характеристикою термодинамічної системи є її теплоємність. Істинною теплоємністю тіла С називають відношення безмежно малої кількості теплоти δQ, одержаної тілом, до відповідного приросту його температури:
Теплоємність тіла масою, рівною одиниці, називають питомою. Частіше використовується мольна теплоємність. Мольною теплоємністю Смол називають кількість теплоти, яка потрібна для нагрівання 1 моля речовини. Вимірюється у Дж/моль·К. Інколи використовують середню теплоємність для інтервалу температур
Якщо система міститься у постійному об’ємі, то кількість теплоти, яка необхідна для підвищення температури на одиницю, виразиться рівнянням:
де СV – ізохорна теплоємність. При сталому тиску система характеризується ізобарною теплоємністю:
де СP – ізобарна теплоємність. Згідно з (1.17) і (1.18), δQV = dU; (1.27) δQP = dH. (1.28) Ізобарна та ізохорна теплоємності, так само як Н і U, відрізняються за величиною роботи, необхідної для зміни об’єму системи. Оскільки в процесі при р = const виконується робота, то для підвищення температури системи на одиницю необхідна більша кількість теплоти, тому СP > CV: CP = CV+R, (1.29) де R – універсальна газова стала. Різниця CP–CV = R є робота ізобарного розширення 1 моля ідеального газу при підвищенні температури на одиницю.
§4. Другий закон термодинаміки. Ентропія. Перший закон термодинаміки констатує збереження енергії при певних перетвореннях, але не дозволяє передбачити здатність фізичних і хімічних процесів до спонтанного перебігу. Другий закон термодинаміки дає можливість з’ясувати напрямок проходження самочинних процесів, а разом з першим – співвідношення між різними макроскопічними параметрами систем у стані термодинамічної рівноваги. С.Карно, досліджуючи умови перетворення теплоти на роботу (1824), прийшов до висновку, що у теплових машинах кількість теплоти, одержана від нагрівача, не може повністю перейти у роботу, частина її передається холодильнику. Якщо позначити Q1 – теплоту, одержану від нагрівання, а Q2 – теплоту, віддану холодильнику, то різниця Q1–Q2 є теплота, яка перетворилася на роботу W. Коефіцієнт корисної дії η можна виразити формулою Карно:
Коефіцієнт корисної дії теплової машини не залежить від природи робочого тіла, а визначається лише інтервалом температур:
де: Т1 – температура нагрівника; Т2 – температура холодильника. Вираз (1.31) повністю узгоджується з формулюванням другого закону термодинаміки, запропонованого Р.Клаузіусом (1850): теплота не може самочинно переходити від холодного тіла до нагрітого. Аналіз формулювань другого закону термодинаміки показує, що всі вони характеризують спрямованість та межі перебігу самочинних процесів, які відбуваються без затрати енергії, наприклад, розширення газу, охолодження гарячого тіла до температури оточуючого середовища. Другий закон стверджує, що теплоту неможливо повністю перетворити у роботу в круговому процесі. Це твердження випливає з природи теплоти і роботи. Ймовірність того, що хаотичний тепловий рух молекул повністю перейде у напрямлений рух дуже мала. Навпаки, напрямлений рух молекул може повністю перейти в хаотичний (робота може повністю перейти в теплоту). Газ самочинно розширюється, але самочинно не стискається, тому що при стисканні хаотичний рух молекул повинен перетворитися у напрямлений. Природність хаотичного руху молекул є причиною того, що різні види енергії прагнуть перейти у теплоту, а теплота передається менш нагрітим тілам. Ці процеси необоротні. Отже, самочинні процеси відбуваються з розсіюванням теплової енергії. Для кількісної характеристики процесів розсіювання енергії Р.Клаузіусом (1865) була введена термодинамічна функція, яку він назвав ентропією і позначив літерою S. Математичний вираз ентропії Клаузіус одержав із циклу Карно, на якому базується робота теплової машини. У загальному вигляді цей вираз можна записати:
де знак нерівності стосується необоротних процесів, а знак рівності – оборотних. Одиниця виміру ентропії – ентропійна одиниця (е.о.), її розмірність Дж/моль·K. Аналогічно іншим термодинамічним функціям (U, H, QP, QV) зміна ентропії ∆S не залежить від шляху процесу, а визначається лише початковим та кінцевим станом системи:
Ентропія є мірою розсіяної (знеціненої) енергії. Чим більша ентропія, тим менша частка енергії може перетворитися в роботу, тобто ентропія виступає як міра необоротності процесу. Самочинно відбуваються лише такі процеси, в яких ентропія зростає: dS > 0. (1.34) Але ентропія є також мірою упорядкованості або термодинамічної ймовірності стану системи. Кожному стану даної системи одночасно відповідає певне значення ентропії, яке тим більше, чим більша ймовірність даного стану системи W. Ймовірність цього макростану системи, що складається з великої кількості мікрочастинок, визначається кількістю способів та варіантів розподілу макрочастинок (молекул, атомів тощо). Л.Больцман встановив зв’язок між ентропією S і ймовірністю стану системи W: S= KlnW, (1.35) де К – стала Больцмана, яка дорівнює відношенню газової сталої R до сталої Авогадро NA Таким чином, ентропія характеризує відносну цінність енергії, яку має система, тобто характеризує ту частину енергії, яка не перетворилася у роботу.
§ 5.Третій закон термодинаміки. Термодинамічні і хімічні потенціали. У 1912 році Планк висунув постулат про те, що при наближенні до абсолютного нуля ентропія So чистої кристалічної речовини без дефектів у кристалічній решітці прямує до нуля: limS = 0, T → 0. Цей постулат одержав назву третього закону термодинаміки. Він стверджує, що при наближенні до абсолютного нуля досягається повна впорядкованість, і макростан кристала чистої речовини може бути реалізований лише одним способом. Ймовірність стану системи (термодинамічна ймовірність) при наближенні до абсолютного нуля дорівнює 1 (W = 1), і тоді, згідно з (1.35), S = Kln1 = 0. Третій закон термодинаміки дає змогу визначити абсолютну ентропію SТ усіх чистих речовин при певній температурі, яка чисельно дорівнює зміні ентропії при рівноважному переході 1 моль кристалічної речовини від абсолютного нуля до даної температури:
де С – молярна теплоємність речовини. За стандартних умов (Т = 298°К і р° = 101,3 кПа) абсолютну ентропію називають стандартною і позначають S°298. Якщо відома стандартна ентропія, можна обчислити значення абсолютної ентропії даної речовини за будь-якої температури:
Ентропія є функцією, яка визначає можливість перебігу самочинного процесу в ізольованій системі. Для закритих систем аналогічними функціями є термодинамічні потенціали: енергія Гельмгольца F (ізохорно-ізотермічний потенціал) і енергія Гіббса G (ізобарно-ізотермічний потенціал). У хімії енергія Гіббса має ширше використання, ніж енергія Гельмгольца, тому що хімічні процеси відбуваються частіше при сталомому тиску, а не при сталому об’ємі. Енергія Гельмгольца і енергія Гіббса виражаються рівняннями: F = U–TS; (1.38) G = H–TS. (1.39) Для розуміння фізичного змісту енергії Гельмгольца здійснюють інтегрування при сталому об’ємі і температурі рівняння: TdS ≥ dU+pdV+δW’, (1.40) яке одержують сполученням рівнянь (1.7) і (1.32): W’ ≤ T(Sкінц–Sпочатк)–(Uкінц–Uпочатк), W’ ≤ (Uпочатк–TSпочатк)–(Uкінц–TSкінц), W’ ≤ Fпочатк–Fкінц або –Fкінц–Fпочатк ≥W’, –ΔF ≥ W’. (1.41) Вираз (1.41) показує, що зменшення енергії Гельмгольца більше або рівне корисній роботі процесу (W’). Таким чином, енергія Гельмгольца характеризує працездатність системи, тобто визначає ту частину енергії, яка в ізохорно-ізотермічному процесі (при V = const i T = const) перетворюється у роботу. Енергію Гіббса можна виразити через енергію Гельмгольца. Для цього слід у виразі (1.39) підставити значення Н із (1.2):
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.47 (0.008 с.) |

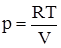 . Якщо цей вираз ввести у (1.10) і проінтегрувати, то отримаємо вираз для ізотермічного розширення 1 моля ідеального газу:
. Якщо цей вираз ввести у (1.10) і проінтегрувати, то отримаємо вираз для ізотермічного розширення 1 моля ідеального газу: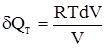 ;
; 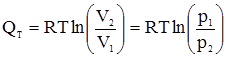 . (1.12)
. (1.12)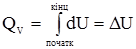 . (1.14)
. (1.14)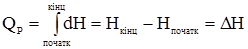 . (1.16)
. (1.16)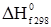 . Верхній індекс 0 показує стандартний стан, а нижній f – початкову літеру слова formation (утворення). За стандартний стан чистої рідкої або кристалічної (твердої) речовини беруть її найбільш стійкий фізичний стан за даної температури і тиску. Як стандартний стан для газу прийнято гіпотетичний стан, при якому газ при p0 = 1,013×105 Па підкоряється законам ідеальних газiв, а його ентальпія дорівнює ентальпії реального газу.
. Верхній індекс 0 показує стандартний стан, а нижній f – початкову літеру слова formation (утворення). За стандартний стан чистої рідкої або кристалічної (твердої) речовини беруть її найбільш стійкий фізичний стан за даної температури і тиску. Як стандартний стан для газу прийнято гіпотетичний стан, при якому газ при p0 = 1,013×105 Па підкоряється законам ідеальних газiв, а його ентальпія дорівнює ентальпії реального газу.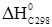 (індекс с – початкова літера слова combustion, тобто згоряння).
(індекс с – початкова літера слова combustion, тобто згоряння).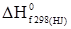 –½
–½ 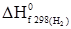 –½
–½ 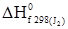 =
= 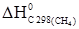 +
+ 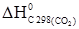 –2
–2 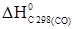 –2
–2 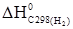 .
.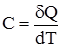 . (1.24)
. (1.24)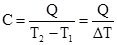 . (1.25)
. (1.25)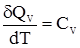 , (1.26)
, (1.26)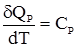 ,
,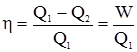 . (1.30)
. (1.30)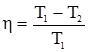 , (1.31)
, (1.31)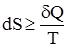 , (1.32)
, (1.32)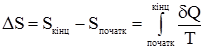 . (1.33)
. (1.33)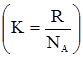 .
.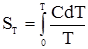 , (1.36)
, (1.36)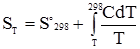 . (1.37)
. (1.37)


