Логарифмический критерий устойчивости. Определение запасов устойчивости по логарифмическим характеристикам

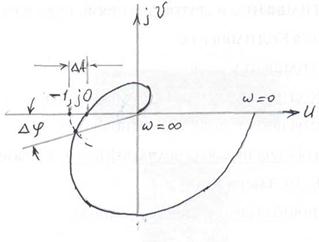
Критерий Найквиста позволяет выяснить устойчивость зам­кнутой системы не только по АФЧХ, но также и по логарифми­ческим частотным характеристикам разомкнутой системы. Эту возможность используют весьма широко вследствие простоты по­строения таких характеристик и определения по ним запаса устой­чивости.

При этом критерий формулируют так: для устойчивости зам­кнутой системы необходимо и достаточно, чтобы при положитель­ных значениях логарифмической амплитудно-частотной характе­ристики разность между числом положительных и отрицатель­ных переходов фазочастотной характеристики через линию —180° равнялись – l /2. Здесь l — число корней с положитель­ной вещественной частью характеристического полинома разом­кнутой системы. Пересечение фазочастотной характеристикой линии —180° снизу вверх считается положительным переходом, а сверху вниз — отрицательным.

Для нормального функционирования всякая система автомати­ческого регулирования должна быть достаточно удалена от гра­ницы устойчивости, должна иметь достаточный запас устойчи­вости.

Необходимость этого обусловлена несколькими причинами:

а) уравнения элементов системы, как правило, идеализированы, при их составлении не учитывают второстепенные факторы;

б) при линеаризации уравнения погрешности приближения дополнительно увеличиваются;

в) параметры элементов определяют с некоторой погрешностью;

г) параметры однотипных элементов имеют технологический разброс;

д) при эксплуатации параметры элементов изменяются вследствие старения.

Следовательно, устойчивая по расчету система в действитель­ности может оказаться неустойчивой.

Запас устойчивости необходим еще и для хорошего качества регулирования.

О запасе устойчивости можно судить, прежде всего, по распо­ложению корней характеристического уравнения системы: чем дальше отстоят они от мнимой оси (в левой полуплоскости), тем больше запас устойчивости.

При синтезе системы выбирают такой запас устойчивости, при котором система функционирует устойчиво и с желаемым качест­вом переходных процессов.

Количественное определение запаса устойчивости зависит от того, какой критерий устойчивости используют. Однако в прак­тике инженерных расчетов наиболее широко применяют опреде­ление запаса устойчивости на основании критерия Найквиста, по удалению амплитудно-фазовой частотной характеристики разом­кнутой системы от точки с ординатами [—1;j0]. Этот факт оценивают двумя показателями: запасом устойчивости по фазе Δφ и за­пасом устойчивости по модулю (амплитуде) ΔА (см. рис.7.2).

Для того чтобы система имела запасы устойчивости Δφ и ΔА, АФЧХ ее разомкнутого контура при удовлетворении критерия устойчивости не должна заходить в часть кольца, ограниченного лучами, проведенными из начала осей координат под углами —180° + Δφ и —180° - Δφ и дугами с радиусами 1 + ΔА и 1 – ΔА.

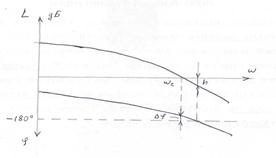
Рис.7.2. Определение запаса устойчивости по АФЧХ

Запасы устойчивости при использовании ЛЧХ определяются по рисунку 7.3.

Рис.7.3. Определение запасов устойчивости по ЛЧХ