Необходимое и достаточное условие устойчивости
Для того чтобы линейная непрерывная система была устойчива необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательные вещественные части: 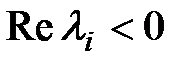 . .
Решение характеристического уравнения степени 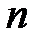 содержит содержит 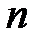 корней. Корни характеристического уравнения могут быть вещественными, комплексными попарно сопряженными, мнимыми, нулевыми. В общем случае корней. Корни характеристического уравнения могут быть вещественными, комплексными попарно сопряженными, мнимыми, нулевыми. В общем случае
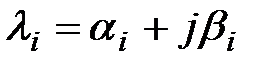 . .
Корни характеристического уравнения, как и всякие комплексные числа можно изобразить в виде точек на комплексной плоскости 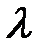 , откладывая по оси абсцисс , откладывая по оси абсцисс 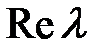 , а по оси ординат , а по оси ординат 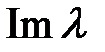 мнимую часть. мнимую часть.
Возможны такие комбинации корней:
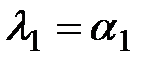 ; ;
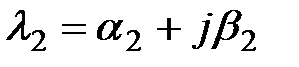
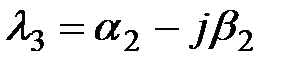
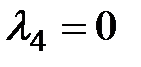
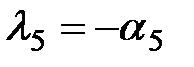
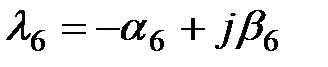
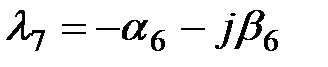
Если все корни разные, то их называют простыми. Если среди корней есть одинаковые, то их называют кратными.
Обычно корни с отрицательными вещественными частями принято называть левыми, поскольку они в комплексной плоскости корней расположены слева от мнимой оси, а корни с положительными вещественными частями – правыми корнями.
Таким образом, условие устойчивости можно сформулировать следующим образом:
Для того чтобы линейная непрерывная система была устойчива необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми, т.е. располагались в левой полуплоскости.
Корни характеристического уравнения равны:
устойчивость система автоматическогоуправления
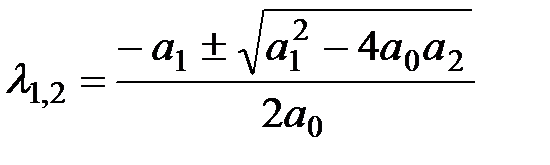
Очевидно, что если 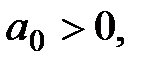 то оба корня левые в том случае когда то оба корня левые в том случае когда 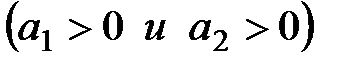 . Аналогично, . Аналогично, 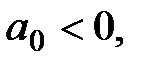 то оба корня левые в том случае когда то оба корня левые в том случае когда 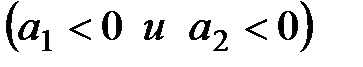
Из рассмотренных примеров следует, что для устойчивости линейных непрерывных систем первого и второго порядков необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были одного знака (или все больше нуля, или все меньше нуля). Это обстоятельство позволяет судить об устойчивости указанных систем без вычисления корней их характеристических уравнений.
Как известно из алгебры, для уравнений третьей и четвертой степеней имеются общие формулы для нахождения корней, а для уравнений пятой степени и выше таких формул нет..
Но и в случае уравнений третьей и четвертой степеней исследование устойчивости путем определения корней неудобно, так как это требует громоздких вычислений. Поэтому для систем выше второго порядка особенно важны условия, которые позволяли бы судить об их устойчивости, не вычисляя корней характеристического уравнения. Такие условия называются критериями устойчивости.
Критерии устойчивости – это критерии, которые позволяют по виду характеристического уравнения или по виду частотных характеристик, судить об устойчивости системы не решая дифференциальных уравнений.
Критерии устойчивости делятся на алгебраические и частотные.
|