Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объекты управления (ОУ). Классификация ОУ входные и выходные переменные ОУ. Статические и динамические свойства ОУ. Понятие математической модели ОУСтр 1 из 23Следующая ⇒
ТАУ Объекты управления (ОУ). Классификация ОУ Входные и выходные переменные ОУ. Статические и динамические свойства ОУ. Понятие математической модели ОУ Объект управления — устройство или динамический процесс, управление поведением которого является целью создания системы автоматического управления.
Классификация систем управления Существует много различных подходов к классификации систем. Например, классификация может основываться на взаимодействии с внешней средой: 1). Изолированная система. Границы такой системы закрыты для экспорта и импорта вещества и энергии (или информации). 2). Закрытая система. Границы ее препятствуют экспорту и импорту вещества, но открыты для энергии (или информации). 3). Открытая система. Такая система обменивается и веществом, и энергией (информацией) с внешней средой. Все управленческие системы являются открытыми, хотя при анализе мы иногда рассматриваем их как закрытые, игнорируя всякое взаимодействие с внешней средой. По возможности адаптации к изменению параметров окружающей среды системы делятся на: 1). Системы с адаптацией; 2). Системы с отсутствием адаптации. Адаптивная система может “адаптироваться” к изменениям среды таким образом, что создается впечатление, что отсутствуют изменения среды. Конечно, это относится к тем изменениям, которые происходят во внешней среде и не касаются внутренних проблем фирмы. По способности возвращаться в исходное состояние системы делятся на: 1) Устойчивые системы; 2) Неустойчивые системы. По наличию обратной связи системы делятся на: · замкнутые; · разомкнутые; · комбинированные.
Входными называются величины, изменение которых приводит к изменению выходных величин. Статические и динамические характеристики систем автоматического управления Для анализа и синтеза САУ необходимо иметь ее математическое описание, т.е. описание процес-сов, протекающих в системе на языке математики. Математическое описание системы может быть задано: - графически (в виде структурных схем); - таблично. Уравнения, а также структурные схемы системы или ее элементов называются математиче-скими моделями. Для получения математической модели системы в ТАУ, в основном, используется поэлементный метод. Этот метод позволяет получать математическую модель системы путем объединения математи-ческих моделей ее отдельных элементов.
Математическую модель отдельных элементов обычно получают: - экспериментально на основе функционального подхода с использованием принципа «черного ящи-ка». При этом математическая модель должна как можно полнее отражать свойства оригинала и в тоже время быть по возможности более простой, чтобы не усложнять исследования. При разработке математической модели системы или ее элементов учитывают два режима ее работы, приведенных на рис. 2.1.
Понятие математической модели ОУ это любой образ, аналог мысленный или установленный изображение, описание, схема, чертеж, карта и т. п. какого либо объема, процесса или явления, используемый в качестве его заменителя или представителя. Сам объект, процесс или явление называется оригиналом данной модели.
Передаточные функции В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях. Преобразование дифференциальных уравнений по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамическиесвойства системы. Передаточной функцией называется отношение изображения выходного воздействия Y(р) к изображению входного X(р) при нулевых начальныхусловиях.
Передаточная функция является дробно-рациональной функцией комплексной переменной:
где:
Передаточная функция имеет порядок, который определяется порядком полинома знаменателя (n).
Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета САР сводится к определению ее передаточной функции. При расчете настроек регуляторов широко используются достаточно простые динамические модели промышленных обьектов управления. В частности, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает в большинстве случаев качественную работу реальной системы управления. В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним из трех видов передаточной функции обьекта управления: 1. В виде передаточной функции инерционного звена первого порядка:
где: К - коэффициент усиления, 2. Для обьекта управления без самовыравнивания передаточная функция имеет вид: 3. Более точнее динамику обьекта описывает модель второго порядка с запаздыванием:
4.
Интегрирующее звено Второго порядка Уравнение звена
Уравнение в операторной форме
Характеристическое уравнение звена
Имеем два корня
Общее решение дифференциального уравнения, определяющее свободное движение (решения однородного дифференциального уравнения), имеет вид
Характер переходного процесса звена зависит от вида корней, которые могут быть действительными или комплексными числами. Если Т 1>2 Т 2, то корни характеристического уравнения будут действительными числами, которые можно представит в виде:
где Т 3 и Т 4 – некоторые условные постоянные времени, причем Т 3> Т 4. Тогда динамическая характеристика звена имеет монотонный апериодический характер и звено называется апериодическим звеном второго порядка. Из уравнения (3.14) получается передаточная функция звена, знаменатель которой можно разложить на два множителя и представить передаточную функцию в следующем виде
где Из (3.19) следует, что инерционное звено второго порядка можно представить как последовательное соединение двух апериодических (инерционных) звеньев первого порядка с постоянными времени Т 3 и Т 4:
где Решение уравнения (3.13) с использованием условных постоянных времени Т 3 и Т 4 при нулевых начальных условиях и однократном ступенчатом воздействии х вх(t)=const имеет вид
Временная характеристика (кривая разгона) представлена на рис. 3.7. Частотные характеристики звена удобно получить из представления последовательного соединения двух апериодических звеньев первого порядка. Частотная передаточная функция, получаемая при замене оператора р величиной j w, также представляется произведением частотных передаточных функций составляющих звеньев
Используя выражение W (j w) через амплитудно-частотную А (w) и фазо-частотную j(w) характеристики, имеем
Следовательно, амплитудно-частотные характеристики последовательно соединенных звеньев перемножаются, а фазочастотные – складываются:
Частотные характеристики апериодических звеньев первого порядка известны. Тогда амплитудно-частотная характеристика апериодического звена второго порядка будет
афазочастотная
Из уравнений (3.25) и (3.26) следует, что при изменении частоты w от 0 до ¥ А (w) изменяется от k (w=0) до 0 (w=¥), а фазовый сдвиг изменяется от 0 (w=0) до –p (w=¥). Апериодическое звено второго порядка так же, как и звено первого порядка, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты.
Инерционными звеньями второго порядка являются обычно такие конструктивные элементы автоматических систем, которые содержат два накопителя вещества или энергии: последовательное соединение двух гидравлических емкостей (рис. 3.8, а) или последовательное соединение двух цепей RС (рис. 3.8, б).
Колебательное звено Понятие устойчивости систем управления. Необходимое и достаточное условие устойчивости линейных систем автоматического управления. Влияние корней характеристического уравнения на характер переходного процесса в системе
Понятие устойчивости На любую систему автоматического управления всегда действуют различные внешние возмущающие воздействия, которые могут нарушать ее нормальную работу. Устойчивость является одним из основных требований, предъявляемых к САУ. Неустойчивые системы не работоспособны. Поэтому важно уметь определять и соответствующим выбором структуры и параметров системы обеспечивать ее устойчивость. В простейшем случае понятие устойчивости связано со способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, она либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.Наглядно устойчивость равновесия может быть представлена следующим образом. Рассмотрим некоторую вогнутую поверхность, в которой расположен шар (рис.1). Положение равновесия шара характеризуется точкой А0. При всяком отклонении шара от положения равновесия, например в точку А1, он будет стремиться снова возвратиться к положению равновесия – в точку А0 (при отсутствии сил трения). Такое положение равновесия устойчиво. Случай, изображенный на рисунке 2 соответствует неустойчивому положению равновесия.
Рисунок 1 Рисунок 2 Критерий Гурвица
1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an; 2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; 3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули. Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица. Рассмотрим примеры применения критерия Гурвица: 1) n = 1 => уравнение динамики: a0p + a1 = 0. Определитель Гурвица: 2) n = 2 => уравнение динамики: a0p2 + a1p + a2 = 0. Определители Гурвица: 3) n = 3 =>уравнениединамики: a0p3 + a1p2 + a2p + a3 = 0. ОпределителиГурвица: Таким образом при n Критерий Гурвица применяют при n
Принцип аргумента Запишем характеристический полином САУ в виде D(p) = a0(p - p1)(p - p2)...(p - pn) = 0. Егокорни pi = i + ji = |pi|ejarg(pi), где arg(pi) = arctg(i/ai) + k, . Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - pi изобразится разностью векторов (рис.68б), где p - любое число.
Еcли менять значение p произвольным образом, то конец вектора p - pi будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как pi - это конкретное неизменное значение. В частном случае, если на вход системы подавать гармонические колебания с различной частотой, то p = j, а характеристический полином принимает вид: D(j) = a0(j - p1)(j - p2)...(j - pn). При этом концы векторов j - pi будут находиться на мнимой оси (рис.68в). Если менять от - до +, то каждый вектор j - pi будет поворачиваться относительно своего начала pi на угол +p для левых и - p для правых корней (рис.68г). Характеристический полином можно представить в виде D(j) = |D(j)|ejarg(D(j)), где |D(j)| = a0|j - p1||j - p2|...|j - pn|, arg(D(j)) = arg(j - p1) + arg(j - p2) +.. + arg(j - pn). Пусть из n корней m - правые, а n - m - левые, тогда угол поворота вектора D(j) при изменении от - до + равен = (n - m) - m, или при изменении от 0 до + получаем = (n - 2m)(/2). Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты от - до + равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на, а при изменении частоты от 0 до + эта разность умножается на /2. Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста. Угол g, образуемый прямой, проходящей через точку пересечения АФЧХ с окружностью единичного радиуса, что соответствует частоте среза системы, и отрицательной вещественной полуосью называется запасом устойчивости системы по фазе.
Типовые входные воздействия
Для оценки качества работы систем управления рассматривают их поведение при некоторых типовых воздействиях. Обычно такими воздействиями служат следующие три основные вида функций: а) ступенчатое воздействие: g(t) =
б) линейное воздействие: g(t) =
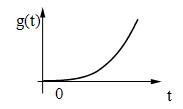
в) квадратичное воздействие:
В некоторых случаях рассматривают обобщенное полиномиальное воздействие:
Ступенчатое воздействие является одним из простейших, но именно с его помощью определяется ряд важных свойств систем управления, связанных с видом переходного процесса. Линейное и квадратичное воздействия часто бывают связаны с задачами слежения за координатами движущегося объекта. Тогда линейное воздействие соответствует движению объекта с постоянной скоростью; квадратичное - движению объекта с постоянным ускорением. Переходные процессы при типовых воздействиях можно построить следующим образом. Пусть задана передаточная функция замкнутой системы управления W(p). Тогда x(p) = W(p) g(p), где g(p) – изображение соответствующего воздействия. Например, если С помощью вычетов или по таблицам находим обратное преобразование Лапласа и получаем вид переходного процесса x(t) для заданного входного воздействия:
гдеRes x(p) – вычет функции x(p) в точке a. Обычно реакция системы на ступенчатое воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
Рис. 21. Переходный процесс, как правило, характеризуют двумя параметрами – длительностью переходного процесса (временем установления) и величиной перерегулирования. Под временем установления tу понимают временной интервал, по истечении которого отклонение |x(t) - xуст | выходного процесса от установившегося значения xуст не превышает определенную величину, например, 0,1gо. Время установления является важным параметром САУ, позволяющим оценить ее быстродействие. Величину tу можно оценить приближенно по амплитудно-частотной характеристике системы. При заданной частоте среза В зависимости от характера собственных колебаний системы переходный процесс в ней может быть колебательным, как это показано на рис. 21, б, или плавным гладким, называемым апериодическим (рис. 21,а). Если корни характеристического уравнения системы действительны, то переходный процесс в ней апериодический. В случае комплексных корней характеристического уравнения собственные колебания устойчивой системы управления являются затухающими гармоническими и переходный процесс в системе имеет колебательный характер. При малом запасе устойчивости САУ ее собственные колебания затухают медленно, и перерегулирование в переходном режиме получается значительным. Как следствие, величина перерегулирования может служить мерой запаса устойчивости системы. Для многих систем запас устойчивости считается достаточным, если величина перерегулирования
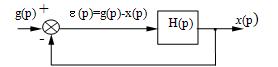
Установившийся режим При проектировании систем управления часто требуется оценить ошибку слежения в установившемся режиме Очень важно, что величина установившейся ошибки может быть легко найдена с помощью теоремы о предельном значении оригинала: При использовании этой теоремы нужно выразить величину ошибки e (p) через g(p). Для этого рассмотрим структурную схему замкнутой системы управления (рис. 22).
Рис. 22 Очевидно, e (p) = g(p) - x(p) = g(p) - H(p)e(p). Отсюда
гдеHe(p) = 1/(1+H(p)); g(p) - изображение типового входного воздействия. Синтез ЛАЧХ в НЧ – области Как известно [1], качество САР в установившемся режиме работы определяется низкочастотной областью ее ЛАЧХ. Решению задачи синтеза в низкочастотной области способствует предлагаемая ниже теорема, позволяющая сравнивать качество двух САР, функционирующих в установившемся режиме. Теорема. Качество установившегося режима лучше у той САР, ЛАЧХ которой в области нижних частот располагается выше. НЧ - область ЛАЧХ это диапазон частот, в котором ЛАЧХ превышает уровень 10 - 20 дБ, т.е. усиление контура САР на этих частотах больше 3 – 10. Если усиление контура САР на нижних частотах меньше 10, то ее качество в установившемся режиме плохое и рассматривать такой случай не имеет смысла. Доказательство. Рассмотрим САР
Рис.1. Схема, позволяющая определить ошибку регулирования e(t) САР при известном задании x Передаточная функция САР рис.1 по ошибке, обусловленной заданием равна:
Для практически полезных систем в НЧ - области |W(jω) | >> 1, поэтому в этой области
Рассмотрим две САР с передаточными функциями по ошибке, обусловленной заданием Фез1(p) и Фез2(p) такие, что в НЧ – области (3) |Фез1(jω)|< |Фез2(jω)|, т.е. качество первой системы выше, чем у второй. Тогда, с учетом (2) (4) |Wез1(jω)|> |Wез2(jω)|. Т.о. частотная характеристика разомкнутого контура в НЧ – области проходит выше у той системы, качество работы в установившемся режиме которой лучше. Следовательно, выше проходит и ЛАЧХ. Наоборот, если выполняется (4), то с учетом (2) выполняется и (3). Теорема доказана.
Рис.2 В установившемся режиме ошибка слежения меньше у той САР, у которой ЛАЧХ в НЧ - области расположена выше Как известно [2], [3], качество САР в установившемся режиме характеризуется коэффициентами ошибок. Чем они меньше, тем качество САР выше. Следствие: коэффициенты ошибок меньше у той САР, частотная характеристика которой в НЧ – области расположена выше и наоборот, если характеристика расположена выше, то коэффициенты ошибок соответствующей САР меньше. Исходными данными для синтеза в НЧ - области являются коэффициенты ошибок по положению с0, по скорости с1 и по ускорению с2. Если требования к установившемуся режиму работы САР заданы в другой форме, то их нужно выразить через коэффициенты ошибок. Например, если задана максимальная ошибка регулирования еm и допустимые отклонения задания Xm, его скорости X1m и ускорения X2m, то привлекая принцип равных влияний не трудно получить верхние границы коэффициентов ошибок:
Коэффициенты ошибок определяют поведение минимально достаточной ЛАЧХ в НЧ – области:
Рис.3. Коэффициенты ошибок определяют минимально достаточную ЛАЧХ в НЧ – области, которая еще способна обеспечить требуемое качество установившегося режима. Системы, у которых ЛАЧХ проходит выше, обеспечивают требуемую точность при отслеживании гладких сигналов Изменяя коэффициент усиления контура исходной САР, т.е. регулируя усиление П – регулятора, следует добиться того, чтобы ЛАЧХ скорректированной САР в НЧ – области располагалась выше минимально допустимой. На этом синтез в НЧ – области завершается. Синтез ЛАЧХ в СЧ – области Качество САР в переходном режиме в основном определяется среднечастотной (СЧ) областью ее ЛАЧХ [1]. СЧ – область это область частот в районе частоты среза ωср, размером примерно от двух октав до двух декад, где значения ЛАЧХ находятся в пределах от -20 дБ до 20 дБ. Традиционная методика построения желаемой ЛАЧХ в среднечастотной области, основывающаяся на применении ряда диаграмм [1], сложна и запутанна. А результаты получаются приближенными. Ниже предлагается простая методика построения ЛАЧХ в среднечастотной области, вытекающая из анализа и композиции традиционных методов. Исходными данными для построения желаемой ЛАЧХ в среднечастотной области являются требования к качеству переходного режима: время регулирования tp и перерегулирование σ. ЛАЧХ на частоте среза ωср должна иметь наклон – 20 дБ/дек. Частота среза ωср может быть определена по приближенной формуле:
Частотный диапазон, в котором желаемая ЛАЧХ в районе частоты среза должна проходить с наклоном – 20 дБ/дек, определяется выражением:
Это требование можно выразить и эквивалентным, предъявляемым к отклонению ЛАЧХ:
Т.о. поведение желаемой ЛАЧХ в СЧ - области полностью, легко и с приемлемой точностью определено:
Рис.4. Поведение желаемой ЛАЧХ в СЧ - области Для получения всей желаемой ЛАЧХ остается припасовать, сопрячь НЧ и СЧ области линией с наклоном, кратным – 20 дБ/дек. Имея желаемую ЛАЧХ, не трудно определить ЛАЧХ корректирующего устройства и реализовать его [1]. Для этого нужно: 1. Поднять ЛАЧХ исходной САР над желаемой в области НЧ на 6 – 10 дБ, обеспечивая некоторый запас. 2. Вычесть из желаемой ЛАЧХ приподнятую, получив тем самым ЛАЧХ корректирующего устройства: (9)
По ЛАЧХ корректирующего устройства не трудно определить его требуемую структуру [1].
ТАУ Объекты управления (ОУ). Классификация ОУ Входные и выходные переменные ОУ. Статические и динамические свойства ОУ. Понятие математической модели ОУ Объект управления — устройство или динамический процесс, управление поведением которого является целью создания системы автоматического управления.
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.204.181 (0.175 с.) |
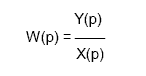
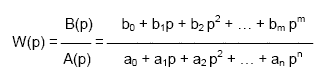
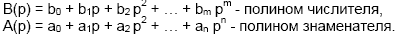
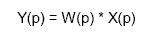
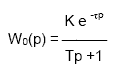
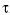 - запаздывание, которые должны быть определены в окрестности номинального режима работы обьекта.
- запаздывание, которые должны быть определены в окрестности номинального режима работы обьекта.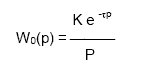
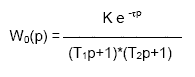
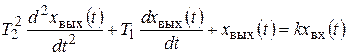 . (3.13)
. (3.13)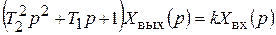 . (3.14)
. (3.14)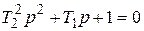 . (3.15)
. (3.15)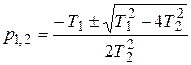 (3.16)
(3.16) . (3.17)
. (3.17)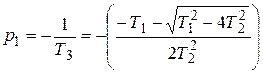 ,
, 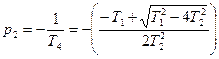 , (3.18)
, (3.18)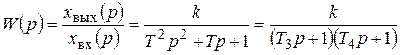 , (3.19)
, (3.19)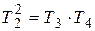 ;
; 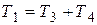 .
.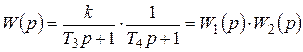 , (3.20)
, (3.20)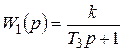 ;
; 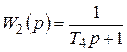 .
.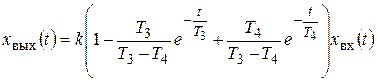 . (3.21)
. (3.21)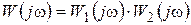 (3.22)
(3.22)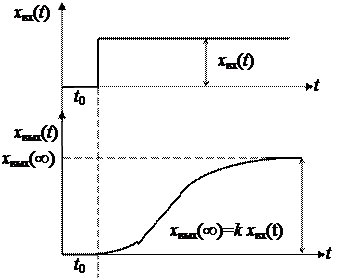
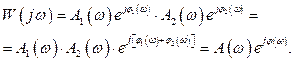 (3.23)
(3.23)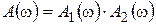 ,
, 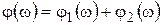 . (3.24)
. (3.24)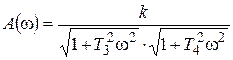 ; (3.25)
; (3.25)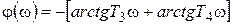 . (3.26)
. (3.26) Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица
Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица 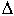 по алгоритму:
по алгоритму: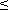 2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия.
2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия. Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя
Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя 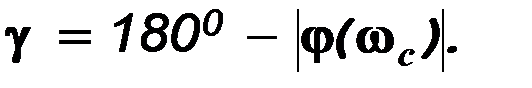 (3.24)
(3.24)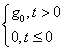 , g(p) =
, g(p) =  ;
;
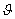 t, t > 0;
t, t > 0;  ;
;
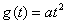 /2, t > 0; g(p) =
/2, t > 0; g(p) = 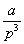 .
.
 , t > 0.
, t > 0. , то
, то  и для g(t) = g0 получим
и для g(t) = g0 получим 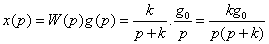 .
.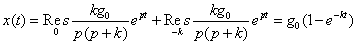 ,
,
 . Для оценки качества системы используется также величина перерегулирования, определяемая соотношением
. Для оценки качества системы используется также величина перерегулирования, определяемая соотношением  .
.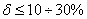 .
. . В зависимости от вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной или бесконечно большой величиной.
. В зависимости от вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной или бесконечно большой величиной.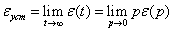 .
.
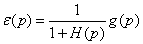 или e (p) = He(p)g(p), где He(p) =
или e (p) = He(p)g(p), где He(p) = 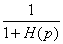 называется передаточной функцией системы управления от входного воздействия g(p) к ошибке слежения e(p). Таким образом, величину установившейся ошибки можно найти с помощью следующего соотношения:
называется передаточной функцией системы управления от входного воздействия g(p) к ошибке слежения e(p). Таким образом, величину установившейся ошибки можно найти с помощью следующего соотношения: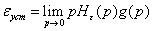 ,
,