
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирующие звенья и их характеристики.Содержание книги
Поиск на нашем сайте
Идеальное дифференцирующее звено.
Реальное дифференцирующее звено.
Апериодические звенья первого и второго порядка. Их уравнения, передаточные функция, временные и частотные характеристики.
1 Порядка Апериодическое (инерционное) звено первого порядка
Апериодическим называется такое звено, у которого выходная величина после подачи на вход ступенчатого воздействия изменяется монотонно, достигая некоторого установившегося значения.
Дифференциальное уравнение в операторной форме
Апериодические звенья первого порядка наиболее часто применяются в практике автоматического регулирования. Примеры звеньев: 1)нагрев тела
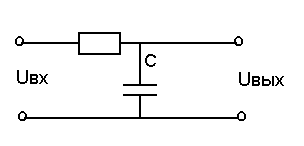
2)RC-цепь
Передаточная функция
Переходная функция
Функция веса
Для рассматриваемого звена временной характеристикой может служить решение дифференциального уравнения (1.70).
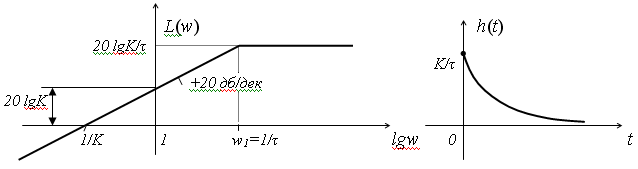
Из выражения (1.75) можно перейти к выражению (1.73), если на вход подать ступенчатое воздействие, а начальные координаты принять равные нулю. Теоретически, переходный процесс у звеньев рассматриваемого типа, длится бесконечно долго. Практически же, для апериодического звена, переходный процесс может быть завершенным, если выходная величина достигает значения 0,95-0,99 от установившегося. Такой промежуток времени определяется значениями (3Т…5Т). Частотные характеристики
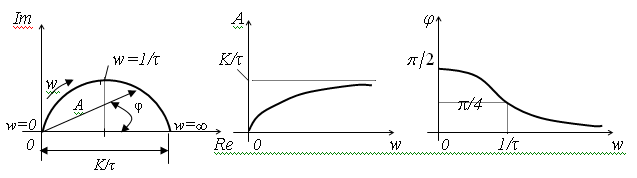
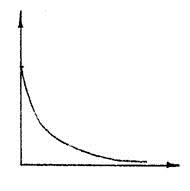
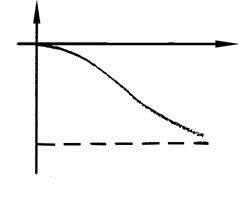
Вид частотных характеристик АФХ АЧХ ФЧХ
Выражение для ЛАЧХ
Выражение для аналитической ЛАЧХ
Вид логарифмических характеристик
Второго порядка Уравнение звена
Уравнение в операторной форме
Характеристическое уравнение звена
Имеем два корня
Общее решение дифференциального уравнения, определяющее свободное движение (решения однородного дифференциального уравнения), имеет вид
Характер переходного процесса звена зависит от вида корней, которые могут быть действительными или комплексными числами. Если Т 1>2 Т 2, то корни характеристического уравнения будут действительными числами, которые можно представит в виде:
где Т 3 и Т 4 – некоторые условные постоянные времени, причем Т 3> Т 4. Тогда динамическая характеристика звена имеет монотонный апериодический характер и звено называется апериодическим звеном второго порядка. Из уравнения (3.14) получается передаточная функция звена, знаменатель которой можно разложить на два множителя и представить передаточную функцию в следующем виде
где Из (3.19) следует, что инерционное звено второго порядка можно представить как последовательное соединение двух апериодических (инерционных) звеньев первого порядка с постоянными времени Т 3 и Т 4:
где Решение уравнения (3.13) с использованием условных постоянных времени Т 3 и Т 4 при нулевых начальных условиях и однократном ступенчатом воздействии х вх(t)=const имеет вид
Временная характеристика (кривая разгона) представлена на рис. 3.7. Частотные характеристики звена удобно получить из представления последовательного соединения двух апериодических звеньев первого порядка. Частотная передаточная функция, получаемая при замене оператора р величиной j w, также представляется произведением частотных передаточных функций составляющих звеньев
Используя выражение W (j w) через амплитудно-частотную А (w) и фазо-частотную j(w) характеристики, имеем
Следовательно, амплитудно-частотные характеристики последовательно соединенных звеньев перемножаются, а фазочастотные – складываются:
Частотные характеристики апериодических звеньев первого порядка известны. Тогда амплитудно-частотная характеристика апериодического звена второго порядка будет
афазочастотная
Из уравнений (3.25) и (3.26) следует, что при изменении частоты w от 0 до ¥ А (w) изменяется от k (w=0) до 0 (w=¥), а фазовый сдвиг изменяется от 0 (w=0) до –p (w=¥). Апериодическое звено второго порядка так же, как и звено первого порядка, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты.
Инерционными звеньями второго порядка являются обычно такие конструктивные элементы автоматических систем, которые содержат два накопителя вещества или энергии: последовательное соединение двух гидравлических емкостей (рис. 3.8, а) или последовательное соединение двух цепей RС (рис. 3.8, б).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.114 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

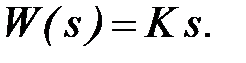

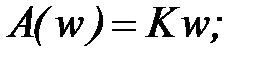
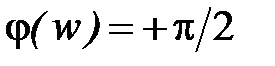
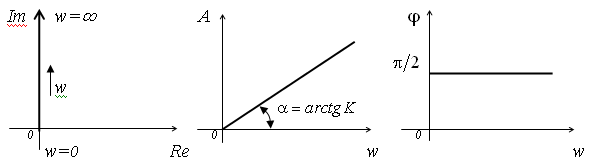
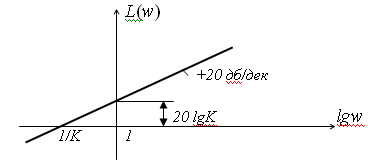
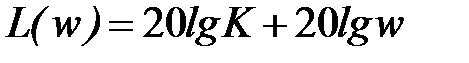
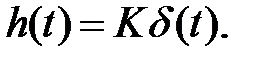
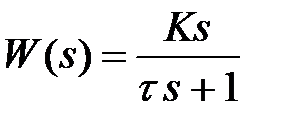
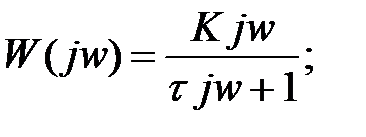
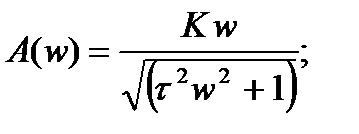
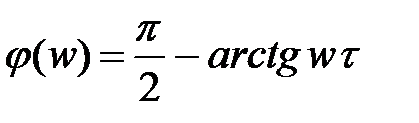
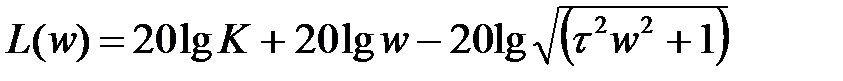
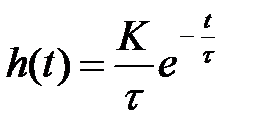
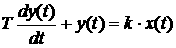 1.70
1.70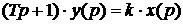 1.71
1.71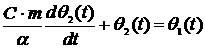
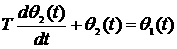
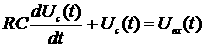
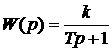 1.72
1.72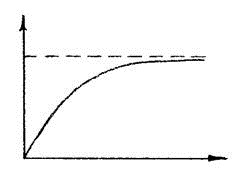
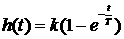 1.73
1.73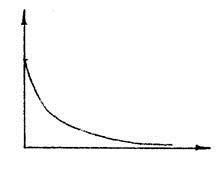
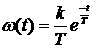 1.74
1.74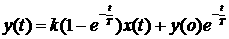 1.75
1.75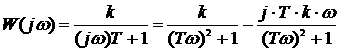 1.76
1.76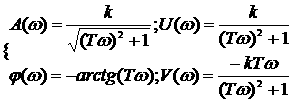 1.77
1.77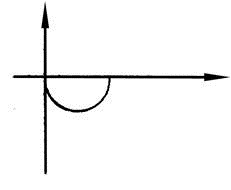
 1.78
1.78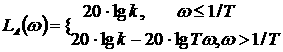 1.79
1.79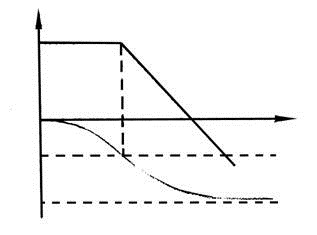
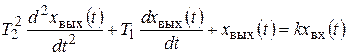 . (3.13)
. (3.13)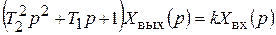 . (3.14)
. (3.14)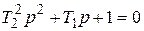 . (3.15)
. (3.15)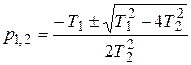 (3.16)
(3.16) . (3.17)
. (3.17)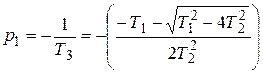 ,
, 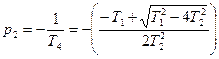 , (3.18)
, (3.18)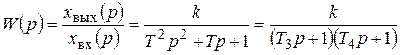 , (3.19)
, (3.19)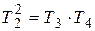 ;
; 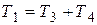 .
.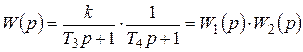 , (3.20)
, (3.20)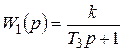 ;
; 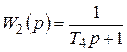 .
.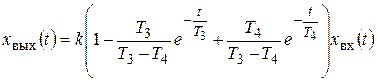 . (3.21)
. (3.21)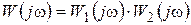 (3.22)
(3.22)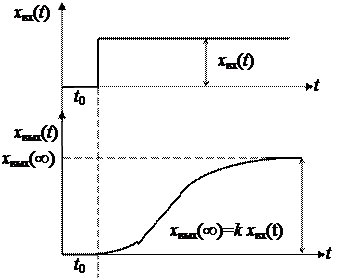
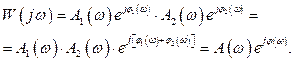 (3.23)
(3.23)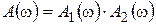 ,
, 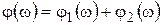 . (3.24)
. (3.24)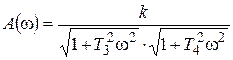 ; (3.25)
; (3.25)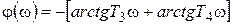 . (3.26)
. (3.26)


