
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические критерии устойчивости. Критерий ГурвицаСодержание книги
Поиск на нашем сайте Необходимое условие устойчивости Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде D(p) = aopn + a1pn-1 + a2pn-2 +... + an = ao(p-p1)(p-p2)...(p-pn) = 0, где p1, p2,..., pn - корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней отрицательны, что можно записать как ai = -|ai| < 0. Подставим их в уравнение: a0 Перемножая комплексно сопряженные выражения, получим: a0 После раскрытия скобок должно получиться выражение a0 Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a0,a1,...,an не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a0> 0, a1 > 0,..., an> 0. В дальнейшем будем рассматривать только уравнения, где a0> 0. В противном случае уравнение домножается на -1. Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерииРауса и Гурвица. Критерий Гурвица
1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an; 2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; 3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули. Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица. Рассмотрим примеры применения критерия Гурвица: 1) n = 1 => уравнение динамики: a0p + a1 = 0. Определитель Гурвица: 2) n = 2 => уравнение динамики: a0p2 + a1p + a2 = 0. Определители Гурвица: 3) n = 3 =>уравнениединамики: a0p3 + a1p2 + a2p + a3 = 0. ОпределителиГурвица: Таким образом при n Критерий Гурвица применяют при n
Принцип аргумента Запишем характеристический полином САУ в виде D(p) = a0(p - p1)(p - p2)...(p - pn) = 0. Егокорни pi = i + ji = |pi|ejarg(pi), где arg(pi) = arctg(i/ai) + k, . Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - pi изобразится разностью векторов (рис.68б), где p - любое число. Еcли менять значение p произвольным образом, то конец вектора p - pi будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как pi - это конкретное неизменное значение. В частном случае, если на вход системы подавать гармонические колебания с различной частотой, то p = j, а характеристический полином принимает вид: D(j) = a0(j - p1)(j - p2)...(j - pn). При этом концы векторов j - pi будут находиться на мнимой оси (рис.68в). Если менять от - до +, то каждый вектор j - pi будет поворачиваться относительно своего начала pi на угол +p для левых и - p для правых корней (рис.68г). Характеристический полином можно представить в виде D(j) = |D(j)|ejarg(D(j)), где |D(j)| = a0|j - p1||j - p2|...|j - pn|, arg(D(j)) = arg(j - p1) + arg(j - p2) +.. + arg(j - pn). Пусть из n корней m - правые, а n - m - левые, тогда угол поворота вектора D(j) при изменении от - до + равен = (n - m) - m, или при изменении от 0 до + получаем = (n - 2m)(/2). Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты от - до + равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на, а при изменении частоты от 0 до + эта разность умножается на /2. Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (p + |a1|)
(p + |a1|)  2)
2)  Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица
Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица 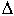 по алгоритму:
по алгоритму: 2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия.
2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия. Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя
Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя 


