Критерий устойчивости Найквиста. Запасы устойчивости

Частотный критерий Найквиста дает возможность определить устойчивость замкнутой АСР по амплитудно-фазовой частотной характеристике АФЧХ разомкнутой системы.

4.4.1Различают три случая использования критерия Найквиста.

а) Разомкнутая система устойчива. В этом случае для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала точку с координатами

 

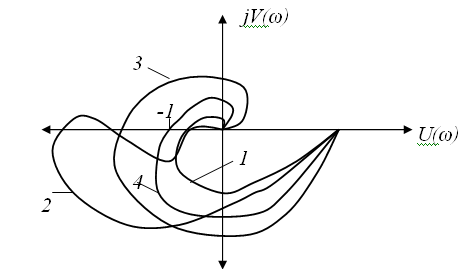
(-1,j0). На рисунке 6 изображены основные из возможных ситуаций.

1-                                           замкнутая система устойчива;

2- замкнутая система условно устойчивая;

З- замкнутая система неустойчива;

4- замкнутая система на границе устойчивости

Рисунок 6 – АФЧХ устойчивых разомкнутых систем

б) Разомкнутая система на границе устойчивости. Характеристический полином такой системы имеет нулевые или

чисто мнимые корни. А у остальных корней отрицательные вещественные части.

        Если нулевых корней ν, то АФЧХ при ω =0 дугой бесконечно большого радиуса перемещается от положительной вещественной полуоси на угол 90ν˚ по часовой стрелке, как показано на рисунке 7.

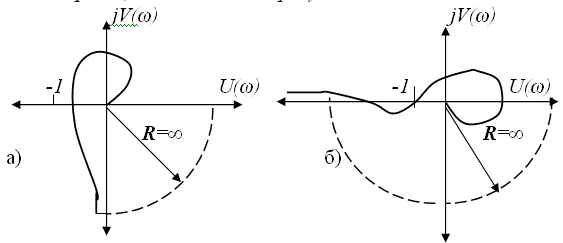
а – замкнутая система устойчива (ν =1);

б – замкнутая система на границе устойчивости (ν =2)

Рисунок 7 – АФЧХ разомкнутых систем, находящихся на границе устойчивости

Для устойчивости замкнутой системы в этом случае необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ∞, дополненная на участке разрыва дугой бесконечного радиуса, не охватывала точку с координатами [–1,j0].

в) Разомкнутая система неустойчивая

В этом случае критерий формулируется так: для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ∞ охватывала точку с координатами [–1,j0] в положительном направлении (против часовой стрелки) l /2 раз, где l – число положительных корней характеристического уравнения.

 Исследование устойчивости системы по критерию Найквиста выполняют по следующему алгоритму.

а) Определяют устойчивость разомкнутой системы.

В одноконтурной системе, составленной из последовательно соединенных звеньев, корни характеристических полиномов этих звеньев являются одновременно корнями характеристического полинома разомкнутой системы. Поэтому, если система не содержит местных обратных связей, определяют корни характеристических полиномов звеньев. Если все корни имеют отрицательную вественную часть, разомкнутая система устойчива. Наличие в структурной схеме интегрирующего звена дает нулевой корень и, следовательно, система будет на границе устойчивости. Если есть хотя бы один корень с положительной вещественной частью, система неустойчива.

б)Преобразуют передаточную функцию разомкнутой системы (2), (4) к виду

b₀p^m+b₁p^m-1+b₂p^m-2+ … +b_m

W(p) = —————————————                            (14)

                       а₀ р ⁿ + a ₁ p^{n -1} + a ₂ p^{n -2} +... +а_n

в) Составляют частотную передаточную функцию разомкнутой системы W (jω), для чего в выражение для передаточной функции разомкнутой системы (14) подставить р= jω.

b₀(j ω) ^m+b₁(j ω)^m-1+b₂(j ω)^m-2+ … +b_mU_I +jV_/

W(j ω) = —————————————————— = ————,(15)

а ₀ (j ω)ⁿ+a₁(j ω)^n-1+a₂(j ω)^n-2+... +a_n      U₂ + jV₂

где                  U_I = b_m- b_m-2 ω ² + b_m-4 ω ⁴ -...;                      V_/ = ω (b_m-1 - b_m-3 ω ² + b_m-5 ω ⁴ -...),                                          U₂ = a_n - а_{п -2} ω ² + а_{п -4} ω ⁴ -...;                     V₂= ω (а_{п -1} - а_{п -3} ω ² + а_{п -5} ω ⁴ -...).

г) Записывают вещественную U(ω) и мнимую V(ω) части частотной передаточной функции W(jω)

        U_IU₂ +V_/V₂

U(ω) = ————— (16)                 

U₂² +V₂²

V_/U₂ –U_IV₂

V(ω) = ————— (17)                  

U₂² +V₂²

д) Подставляя в (16) и (17) различные значения частоты ω от 0 до ∞, расчитывают координаты для построения АФЧХ разомкнутой системы. При этом целесообразно сначала определить характерные точки АФЧХ: ее точки при предельных значениях частоты (ω = 0, ω = ∞), точки пересечения АФЧХ осей координат. Далее вычисляют дополнительные точки для более точного построения АФЧХ.

Для определения точек пересечения вещественной оси (оси абсцисс) необходимо приравнять нулю мнимую часть комплексной частотной функции W (jω) V (ω) = 0, по полученному выражению вычислить частоты, при которых справедливо это равенство, затем вычислить значения U(ω) на этих частотах. Для расчета точек пересечения АФЧХ мнимой оси приравнивают нулю вещественную часть U (ω) = 0.

ж) Результаты расчета записывают в таблицу 2.

з) По данным таблицы 2 стрят АФЧХ.

Каждому значению частоты будет соответствовать точка на комплексной плоскости. Соединив точки плавной кривой, получим годограф. Рядом с точкой на годографе указывается соответствующая частота. Таким образом, полученный годограф будет представлять АФЧХ разомкнутой системы.

и) Делают заключение об устойчивости системы, применяя соответствующую формулировку критерия.

Запасы устойчивости.

Устойчивость замкнутой САУ зависит от расположения годографа АФЧХ разомкнутой системы относительно критической точки. Чем ближе эта кривая проходит от критической точки, тем ближе замкнутая САУ к границе устойчивости. Для устойчивых систем удаление АФЧХ разомкнутой системы от критической точки принято оценивать запасами устойчивости по фазе и по модулю.

Допустим, что АФЧХ некоторой разомкнутой системы имеет вид, показанный на рис. 3.12.

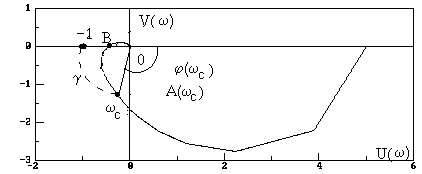
     Рис. 3.12. АФЧХ разомкнутой системы

Угол g, образуемый прямой, проходящей через точку пересечения АФЧХ с окружностью единичного радиуса, что соответствует частоте среза системы, и отрицательной вещественной полуосью называется запасом устойчивости системы по фазе.

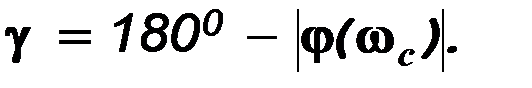                                   (3.24)