
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение временных характеристик
Временные характеристики – импульсная переходная функция w (t) и переходная характеристика h (t) могут быть получены экспериментально, если удается подать на вход объекта воздействие в виде достаточно узкого импульса с необходимой амплитудой или ступенчатой функцией времени. Последнее более реально – функцию веса w (t) впоследствии можно получать дифференцированием функции h (t). Статистические методы непараметрической идентификации позволяют оценить ординаты функции веса w (t) путем обработки данных вход-выход объекта в виде случайных сигналов, возможных в режиме нормальной эксплуатации (корреляционный анализ). Существуют методы построения временных характеристик по частотным, базирующиеся на обратном преобразовании Фурье. В случае, когда исходная информация об объекте представлена в форме дифференциального уравнения (1), временные характеристики получают его решением. В классической теории автоматического управления для решения дифференциальных уравнений часто привлекают так называемый операторный метод, связанный с преобразованием Лапласа. Метод особенно удобен в случае типовых воздействий в виде обобщенных функций и позволяет легко учесть ненулевые начальные условия. Пусть дано дифференциальное уравнение n -порядка звена или системы автоматического управления (2). Необходимо получить выражения для импульсной переходной функции (функции веса) w (t), переходной характеристики h (t), а также для реакции в случае воздействия общего вида. Пусть изображение по Лапласу воздействия на входе системы или звена представляет собой дробно-рациональную функцию от s:
Если преобразовать по Лапласу дифференциальное уравнение n -го порядка при ненулевых предначальных условиях, то после разрешения полученного алгебраического уравнения относительно изображения переменной выхода имеем
Здесь полином AH (s) определяется предначальными условиями. Если все предначальные условия нулевые, то изображение выхода
где W (s) – передаточная функция. Искомое решение – переменная на выходе системы (оригинал) получается обратным преобразованием Лапласа:
где с – абсцисса сходимости. Формула обращения Римана – Меллина устанавливает однозначное соответствие между оригиналом и изображением в точках непрерывности оригинала. Имеются алгоритмы и программы, позволяющие вычислять интеграл (8) при произвольных функциях Y (s). Практическое вычисление оригинала у (t) удобно производить, основываясь на теореме о вычетах, согласно которой значение интеграла (8) может быть представлено суммой вычетов подынтегральной функции,
где ResY (s) – вычет функции Y (s) в полюсе si; i= 1,..., nY; nY – число полюсов изображения Y (s); при t <0 функция у (t) = 0. Для обыкновенных линейных дифференциальных уравнений и типовых воздействий изображение Y (s) является дробно-рациональной функцией, которую можно представить в виде суммы простейших дробей:
где
Оригинал y (t) в соответствии с разложением (9) имеет вид:
Импульсная переходная функция (функция веса) w (t) представляет собой реакцию системы на Разложение передаточной функции на сумму простейших дробей в случае простых полюсов si; i = 1, …, n имеет вид:
где Ci – коэффициент разложения (вычета),
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.143.239 (0.003 с.) |
 .
. . (7)
. (7)
 (8)
(8) ,
, , (9)
, (9)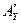 – производная полинома AY по s; si – простые полюсы;
– производная полинома AY по s; si – простые полюсы;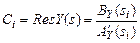
 .
. -функцию при нулевых начальных условиях. Поскольку изображение
-функцию при нулевых начальных условиях. Поскольку изображение  , то функция веса представляет собой обращение по Лапласу передаточной функции и
, то функция веса представляет собой обращение по Лапласу передаточной функции и 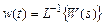 .
.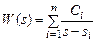 , (10)
, (10)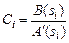 . (11)
. (11)


