Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод фазовой плоскости для анализа поведения нелинейных систем⇐ ПредыдущаяСтр 23 из 23 В системах управления, наряду с линейными ПИД законами регулирования, применяются нелинейные законы регулирования, среди которых наиболее распространены релейные законы. Релейные законы имеют две разновидности: двухпозиционный закон регулирования и трехпозиционный. При этом система становится принципиально нелинейной. Нелинейными свойствами могут также обладать объекты управления или технологические процессы. Применение релейных законов регулирования во многих случаях позволяет решить задачу автоматического регулирования простым способом при высоком быстродействии. Релейные законы дают возможность добиться таких результатов, которые принципиально не могут быть достигнуты при помощи линейных регуляторов. Динамический процесс при релейном регуляторе может быть сходящимся к положению равновесия или расходящимся в зависимости не только от значений параметров системы, но и от величины начальных условий. Поэтому исследование динамики нелинейных систем автоматического регулирования более удобно производить с помощью метода фазовой плоскости. Достоинство данного метода заключается в возможности получения достаточно полного решения при высокой точности. Однако исследовать нелинейные системы с помощью построения фазового портрета удобно лишь для систем второго порядка, когда фазовые траектории размещаются на плоскости. Для более высоких порядков фазовые траектории могут быть построены в пространстве, в связи с чем возрастают трудности анализа. Фазовый портрет систем с релейным законом изображается на плоскости, имеющей две координатные оси. На горизонтальной оси откладывается регулируемый параметр У, а на вертикальной оси – его производная dy/dt, т. е. скорость изменения регулируемого параметра. Характер фазовых траекторий определяется видом исходного уравнения системы, начальное положение точки на фазовой плоскости определяется начальными условиями. Фазовая плоскость с траекториями в целом соответствует общему решению системы и характеризует совокупность всех возможных движений. Построив фазовые траектории, можно проследить, как движется по ним изображающая точка относительно точки покоя. Если изображающая точка с течением времени неограниченно удаляется от точки покоя, соответствующее равновесное состояние неустойчиво. Наоборот, если изображающая точка, независимо от ее начального положения, двигаясь по фазовой траектории, приходит к точке покоя, состояние равновесия устойчиво. Точкой покоя считается изолированная особая точка с координатами у = 0, dY/dt = 0.
Разработан и применяется ряд методов определения автоколебаний и устойчивости нелинейных систем. Наиболее простым из них является метод, разработанный Л.С. Гольдфарбом. Этот метод является графическим, обладает хорошей наглядностью и сравнительной простотой. Также он может быть использован для приближенного анализа нелинейных систем управления. В этом случае структура системы имеет вид, представленный на рис. 3.3. В структуре показан нелинейный элемент с передаточной функцией WH и линейный элемент с непрерывной передаточной функцией W(S). Общее аналитическое нелинейной системы может быть представлено следующим способом:
U (t) = F [D(t)]. (3.1)
Относительно изображений уравнение (3.1) примет вид
U (p) = L { F [ D (t)]} =
На выходе линейной части сигнал y (p) определяется уравнением
y (p) = W (p) u (p), (3.3)
где W (p) – передаточная функция линейной части. С учетом уравнения (3.2) уравнение (3.3) примет вид:
y (p) = W (p) u (p) = W (p) L { F [ D (t)]} = W (p)
где D(t) = x (t) – y (t) или в пространстве изображений D(p)= x (p) – y (p). Уравнение (3.4) является нелинейным, поскольку в него входит изображение D(t) и нелинейная функция F [D(t)]. При переводе уравнения (3.4) к оригиналу согласно теореме свертывания преобразования Лапласа получим
y (t) =
Уравнение (3.5) является интегральным нелинейным и не имеет общих методов решения. Они могут быть получены численными методами или с помощью программных комплексов с применением персональных компьютеров. Уравнение свободных колебаний (характеристическое уравнение) замкнутой системы имеет следующий вид:
где W(jω) – частотная передаточная функция линейной части; WH(а) – эквивалентная частотная передаточная функция нелинейной части. Представим выражение (3.6) в виде уравнения Гольдфарба:
W (j ω ) = – GH (a), (3.7)
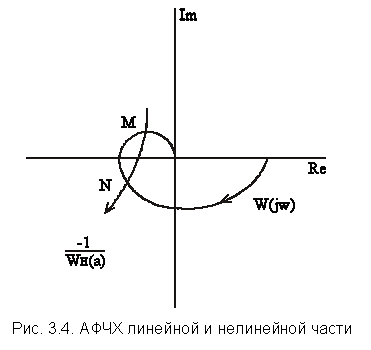
где GH (a) = 1 / WH (a). Уравнение (3.7) решается графически. Для этого на комплексной плоскости строится АФЧХ линейной части при изменении ω от 0 до ∞ и обратная АФЧХ нелинейной части при изменении а от 0 до ∞, где а – амплитуда гармонического воздействия. Точка пересечения кривых АФЧХ определяет амплитуду и частоту возможных автоколебаний. Если точки пересечения нет, то автоколебания невозможны. Критерий устойчивости Гольдфарба формулируется следующим образом. Если линейная часть разомкнутой системы устойчива, то точка пересечения характеристик W(j ω ) и –1 /WН(a) соответствует устойчивым автоколебаниям, когда в этой точке характеристика –1 /WН(a) выходит из контура W(jω). Если же в точке пересечения характеристика –1 /WН(a) входит в контур W(jω), то такая точка соответствует неустойчивым автоколебаниям. Сформулированный критерий Гольдфарба является необходимым, но недостаточным. Однако в большинстве практических задач указанный критерий оказывается достаточным, причем тем вероятнее, чем больше фильтрующие свойства линейной части системы. Эквивалентная частотная передаточная функция нелинейного элемента может быть представлена в следующем виде:
где q(a) – модуль эквивалентной частотной передаточной функции (эквивалентная амплитудная частотная характеристика); М(а) – аргумент эквивалентной частотной передаточной функция (эквивалентная фазовая частотная характеристика). Вид q(a) и М(а) зависит от типа нелинейности, в частности, для двухпозиционного релейного регулятора M (a) = 0. Для трехпозиционного релейного регулятора
M (a) = 0.
На рис. 3.4. представлены АФЧХ линейной и нелинейной части, иллюстрирующие применение метода Гольдфарба. На рис. 3.4 точка М соответствует неустойчивым колебаниям, а точка Nсоответствует устойчивым автоколебаниям. Таким образом, рассмотренный подход позволяет производить анализ процессов и выявить особенности поведения нелинейных систем.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.245.196 (0.005 с.) |

 . (3.2)
. (3.2)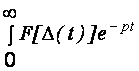 dt, (3.4)
dt, (3.4) . (3.5)
. (3.5) , (3.6)
, (3.6) , (3.8),
, (3.8), ;
; ;
; Решение уравнения y(x) + C, содержащее постоянную интегрирования C, описывает фазовую траекторию. Если это описание получено, то строя графики при разных C, можно построить фазовый портрет системы. Основная сложность описанного подхода заключается в необходимости решения нелинейного дифференциального уравнения фазовой траектории, что представляет определенные трудности.
Решение уравнения y(x) + C, содержащее постоянную интегрирования C, описывает фазовую траекторию. Если это описание получено, то строя графики при разных C, можно построить фазовый портрет системы. Основная сложность описанного подхода заключается в необходимости решения нелинейного дифференциального уравнения фазовой траектории, что представляет определенные трудности.
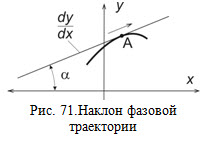 Для исключения необходимости решения дифференциального уравнения при построении фазовых траекторий используется метод изоклин. На рис. 71 показан фрагмент фазовой траектории. Если рассматривать произвольную точку A фазовой траектории, то направление траектории в этой точке можно определить, проведя касательную к фазовой траектории в рассматриваемой точке. Для этой касательной
Для исключения необходимости решения дифференциального уравнения при построении фазовых траекторий используется метод изоклин. На рис. 71 показан фрагмент фазовой траектории. Если рассматривать произвольную точку A фазовой траектории, то направление траектории в этой точке можно определить, проведя касательную к фазовой траектории в рассматриваемой точке. Для этой касательной
 Таким образом, направление фазовой траектории в произвольной ее точке можно задать углом наклона α касательной, проведенной к фазовой траектории в этой точке. Вместо угла наклона удобнее использовать константу c. Если на фазовой плоскости соединить линией все точки, в которых фазовая траектория имеет одинаковое направление (одно и то же значение константы c), то мы получим изоклину – линию равных углов наклона касательной к фазовой траектории.
Уравнение изоклины
c=f(x,y),
где f(x,y) – правая часть дифференциального уравнения фазовой траектории.
Например, если дифференциальное уравнение фазовой траектории
Таким образом, направление фазовой траектории в произвольной ее точке можно задать углом наклона α касательной, проведенной к фазовой траектории в этой точке. Вместо угла наклона удобнее использовать константу c. Если на фазовой плоскости соединить линией все точки, в которых фазовая траектория имеет одинаковое направление (одно и то же значение константы c), то мы получим изоклину – линию равных углов наклона касательной к фазовой траектории.
Уравнение изоклины
c=f(x,y),
где f(x,y) – правая часть дифференциального уравнения фазовой траектории.
Например, если дифференциальное уравнение фазовой траектории
 Уравнение изоклины алгебраическое. Задавая разные значения константы можно построить семейство изоклин на фазовой плоскости, каждая из которых характеризует определенное направления фазовой траектории. Пример построения семейства изоклин приведен на рис. 72. Стрелками указано направление фазовой траектории в точках изоклины.
Уравнение изоклины алгебраическое. Задавая разные значения константы можно построить семейство изоклин на фазовой плоскости, каждая из которых характеризует определенное направления фазовой траектории. Пример построения семейства изоклин приведен на рис. 72. Стрелками указано направление фазовой траектории в точках изоклины.
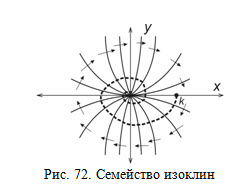 Для построения фазовой траектории задают ее начальную точку, соответствующую начальным условиям для исследуемой системы (точка k на рис. 72). Затем из этой точки проводят отрезок прямой в сторону ближайшей изоклины параллельно стрелке, определяющей направление фазовой траектории в точках этой изоклины. Линия проводится примерно до середины промежутка между изоклинами.
Конец отрезка принимают за начальную точку следующего отрезка, который строят по описанному алгоритму. Полученная ломаная линия сглаживается до получения линии фазовой траектории.
Метод изоклин прост, т.к. не требует решения дифференциального уравнения. Однако, он требует значительного объема графических построений. Одновременно метод изоклин является методом приближенного построения фазовых траекторий, что следует учитывать при его использовании.
Для построения фазовой траектории задают ее начальную точку, соответствующую начальным условиям для исследуемой системы (точка k на рис. 72). Затем из этой точки проводят отрезок прямой в сторону ближайшей изоклины параллельно стрелке, определяющей направление фазовой траектории в точках этой изоклины. Линия проводится примерно до середины промежутка между изоклинами.
Конец отрезка принимают за начальную точку следующего отрезка, который строят по описанному алгоритму. Полученная ломаная линия сглаживается до получения линии фазовой траектории.
Метод изоклин прост, т.к. не требует решения дифференциального уравнения. Однако, он требует значительного объема графических построений. Одновременно метод изоклин является методом приближенного построения фазовых траекторий, что следует учитывать при его использовании.