
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 19. Нормальные напряжения при прямом изгибе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчёты на прочность. Рассмотрим изогнутый брус (рисунок 51). В нём можно выделить три области: 1. 2. Область сжатых продольных волокон. Это такая область, в которой изогнутые продольные волокна бруса стали короче. 3. 3. Нейтральный слой. Это такая область, в которой изогнутые Рисунок 57. Изогнутый брус. Продольные волокна не изменили своей длины.
l = dz +𝛥 Рисунок 58. Распределение нормальных Напряжений по поперечному сечению бруса. Относительная продольная деформация волокна mm составит: 𝜀 =
Осевым моментом инерции поперечного сечения называется интеграл, взятый по всей площади сечения от произведения площади элементарной площадки на квадрат расстояния от неё до оси. Рассмотрим прямоугольное поперечное сечение бруса с размерами b и h. Выделим в этом сечении элементарную площадку по всей ширине толщиной dy (рисунок 59). Площадь элементарной площадки dA = bdy. Тогда осевой момент инерции относительно оси Х определится как:
Аналогично можно определить осевой момент инерции
В этом случае элементарную площадку следует выделить по всей высоте сечения параллельно оси Y. Пределы интегрирования необходимо выбрать от -
Рисунок 59. Прямоугольное сечение. Рассмотрим круглое поперечное сечение бруса (рисунок 60).
Полярный момент инерции круглого поперечного сечения определяется по формуле: Учитывая, что Интегралы, стоящие в правой части называются осевыми моментами инерции и обозначаются IyuIx. Поскольку круг фигура правильная, величины осевых моментов инерции для него равны, т. е. Iy = Ix = Осевые моменты сопротивления круглого поперечного Сечения так же равны и определяются по формуле: Рисунок 60. Круглое сечение. Расчёты на прочность при изгибе проводятся по нормальным напряжениям. В основе расчётов на прочность при изгибе лежит условие прочности: РН ≤ ДН (рабочие напряжения должны быть меньше, или равны допускаемым напряжениям). Рассмотрим виды расчётов и формулы для балок, поперечные сечения которых симметричны относительно нейтрального слоя. Различают три вида расчётов на прочность: 1. Проверочный расчёт 2. Проектный расчёт Для круглого поперечного сечения Для прямоугольного поперечного сечения Следовательно, b = Для поперечных сечений балок, изготовленных из фасонного прокатного профиля (двутавр, швеллер) размеры поперечного сечения подбирают по таблицам сортамента по величине 3. Определение допускаемой нагрузки.
Пример решения задачи. Для балки на двух опорах (рисунок 50) подобрать из условия прочности круглое, прямоугольное с отношением размеров
РЕШЕНИЕ. Производим проектный расчёт на прочность при изгибе для опасного сечения бруса, положение которого определяем по эпюре изгибающего момента. Опасным сечением будет то, в котором абсолютная величина изгибающего момента будет наибольшей. Формула проектного расчёта:
проходящей через нейтральный слой его поперечного сечения; МХ О (Нмм) – изгибающий момент в опасном поперечном сечении бруса;
Определим осевой момент сопротивления опасного сечения: Круглое поперечное сечение: Прямоугольное поперечное сечение:
Двутавр – зто стандартный фасонный прокатный профиль. По таблице23 сортамента выбираем двутавр, у которого осевой момент сопротивления Wx ближайший больший к расчётному. В нашем случае подходит двутавр №33, у которого Wx = 597 cм3. Экономическую эффективность подобранных поперечных сечений бруса определим, сравнив их площади:
Вывод: наиболее экономичным для заданного бруса будет двутавровое поперечное сечение, т. к. его площадь наименьшая из трёх рассматриваемых вариантов. Задача для самостоятельного решения. Для расчётной схемы балки, рассчитанной по рисунку 19 подобрать из условия прочности круглое, прямоугольное с отношением сторон ½ и двутавровое поперечное сечение. Сравнить их экономическую эффективность. Допускаемое напряжение
|
||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.117 (0.012 с.) |

 Область растянутых продольных волокон. Это такая область, в которой изогнутые продольные волокна бруса стали длиннее.
Область растянутых продольных волокон. Это такая область, в которой изогнутые продольные волокна бруса стали длиннее. Возьмём изогнутый брус бесконечно малой длины (рисунок 21). Крайние поперечные сечения соединим в точке, угол между ними обозначим d𝜃. Радиус нейтрального слоя обозначим 𝜌. Тогда радиус волокна mm составит 𝜌 + y. Длина волокна nn, расположенного в нейтральном слое,
Возьмём изогнутый брус бесконечно малой длины (рисунок 21). Крайние поперечные сечения соединим в точке, угол между ними обозначим d𝜃. Радиус нейтрального слоя обозначим 𝜌. Тогда радиус волокна mm составит 𝜌 + y. Длина волокна nn, расположенного в нейтральном слое,  . Длина волокна mm, расположенного в растянутой области,
. Длина волокна mm, расположенного в растянутой области, =
= 
 =
=  =
=  . Тогда формула закона Гука для нормальных напряжений примет вид: 𝛔 = Е𝜀 = Е
. Тогда формула закона Гука для нормальных напряжений примет вид: 𝛔 = Е𝜀 = Е  в точках, наиболее удаленных от нейтрального слоя. Нейтральный слой расположен на главной центральной оси поперечного сечения, перпендикулярной нагрузке. Для поперечных сечений, симметричных относительно нейтрального слоя максимальные напряжения в растянутой и сжатой областях равны и определяются по формуле:
в точках, наиболее удаленных от нейтрального слоя. Нейтральный слой расположен на главной центральной оси поперечного сечения, перпендикулярной нагрузке. Для поперечных сечений, симметричных относительно нейтрального слоя максимальные напряжения в растянутой и сжатой областях равны и определяются по формуле: , где
, где  - осевой момент сопротивления поперечного сечения бруса относительно оси Х, проходящей через нейтральный слой.
- осевой момент сопротивления поперечного сечения бруса относительно оси Х, проходящей через нейтральный слой. =
=  =
=  .
. относительно оси Y.
относительно оси Y. 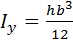 .
. до
до  Выделим внутри сечения элементарную площадку dA. Расстояние от неё до центра сечения обозначим 𝜌, расстояние до оси Х обозначим y, а расстояние до оси Y обозначим х.
Выделим внутри сечения элементарную площадку dA. Расстояние от неё до центра сечения обозначим 𝜌, расстояние до оси Х обозначим y, а расстояние до оси Y обозначим х. .
. , получим::
, получим:: 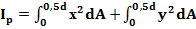 .
. =
=  ≈ 0,05
≈ 0,05  .
.
 ≤
≤  Цель проверочного расчёта проверить соблюдение условия прочности.
Цель проверочного расчёта проверить соблюдение условия прочности. . Цель расчёта определить размеры опасного поперечного сечения балки, обеспечивающих прочность.
. Цель расчёта определить размеры опасного поперечного сечения балки, обеспечивающих прочность. , следовательно, d =
, следовательно, d = 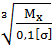 .
. . Для прямоугольного поперечного сечения с соотношением размеров h/b = 2 осевой момент сопротивления
. Для прямоугольного поперечного сечения с соотношением размеров h/b = 2 осевой момент сопротивления  =
= 
 .
. . Цель расчёта определить грузоподъёмность балки при условии соблюдения её прочности.
. Цель расчёта определить грузоподъёмность балки при условии соблюдения её прочности. и двутавровое поперечные сечения, если допускаемое напряжение для материала бруса
и двутавровое поперечные сечения, если допускаемое напряжение для материала бруса  Н/мм2. Сравнить экономическую эффективность применения подобранных поперечных сечений бруса.
Н/мм2. Сравнить экономическую эффективность применения подобранных поперечных сечений бруса.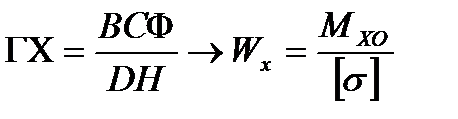 , где
, где (мм3) – осевой момент сопротивления поперечного сечения бруса относительно оси Х,
(мм3) – осевой момент сопротивления поперечного сечения бруса относительно оси Х,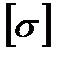 (Н/мм2) – допускаемое напряжение для материала бруса.
(Н/мм2) – допускаемое напряжение для материала бруса. мм3
мм3 мм
мм мм
мм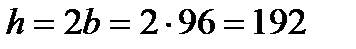 мм.
мм. мм2 = 254,34 см2
мм2 = 254,34 см2 мм2 = 184,32 см2
мм2 = 184,32 см2 см2 - по таблице сортамента для двутавра №33.
см2 - по таблице сортамента для двутавра №33.


