Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эпюры поперечной силы и изгибающего момента.Содержание книги
Поиск на нашем сайте
Балка жёстко закреплена одним концом. Эпюры поперечной силы и изгибающего момента строятся в следующем порядке: 1. Параллельно оси бруса проводятся две нулевые линии и переносятся на них точки приложения внешних сил и моментов, а также границы равномерно распределённой нагрузки. В результате этого вся длина бруса разбивается на несколько характерных участков. 2. Применяя метод сечений, начиная со свободного конца бруса, отбрасывая всё время его закреплённую часть, используя изложенные выше четыре правила, определяются значения поперечной силы и изгибающего момента на границах характерных участков: 1 участок (рисунок 52).2 участок (рисунок 53).
Рисунок 52. 1 участок. Рисунок 53. 2 участок.
Qy1 = F = 20 кН. Mx1 = - Fz1. Q = q (z2 – 2) при z1 = 0 Mx1 = 0 Qy2 = F – Q = F – q(z2 – 2) при z2 = 2 м Мх1 = - при z2 = 6 м Qy2 = 20 – 20(6 – 2) = - 60 кН У нас получилось, что на втором характерном участке эпюра поперечной силы, изменяясь непрерывно, пересекает нулевую линию (рисунок 55). Это значит, что на эпюре изгибающего момента в этом месте будет экстремум (максимум или минимум). Необходимо определить координату zЭ этой точки. Для этого приравняем нулю выражение поперечной силы на этом участке: Теперь составим выражение изгибающего момента для второго характерного участка (рисунок 43): При z2 = 2 м. Мх2 = - При z2 = zЭ = 3 м. Мх2 = - При z2 = 6 м. Мх2 = -
Рисунок 54. 3 участок.
При z3 = 6 м. Мх3 = При z3 = 10 м. Мх3 = По полученным результатам строятся эпюры поперечной силы и изгибающего момента (рисунок 55).
Рисунок 55. Расчётная схема бруса, эпюры Qy и Mx Задача для самостоятельного решения. Для одной из схем балки (рисунок 56) по заданным величинам (таблица 16) построить эпюры поперечной силы и изгибающего момента. Таблица 16. Варианты задания
Рисунок 55. Расчётные схемы для задания. Балка на двух опорах. Построить эпюры поперечной силы и изгибающего момента для балки, имеющей две опоры и нагруженной так, как показано на рисунке 18. Исходные данные: F1 = 18 кН, F2 = 30 кН, М1 = 20 кНм, М2 = 10 кНм.
РЕШЕНИЕ. Заданная балка не нагружена равномерно распределённой нагрузкой. В этом случае эпюры поперечной силы и изгибающего момента удобно строить по характерным точкам. Характерные точки это точки приложения внешних сил и моментов, т. е. границы характерных участков. При построении эпюр необходимо использовать следующие дополнительные правила: 1. Эпюра поперечной силы на любом участке бруса представляет собой прямую, параллельную нулевой линии. 2. В том месте, где приложена внешняя нагрузка на эпюре поперечной силы будет скачок на её величину вверх, если она действует вверх, или вниз, если она действует вниз (правило «прямых скачков» при построении эпюры слева направо). При построении эпюры поперечной силы справа налево действует правило «обратных скачков», т. е. скачки происходят в направлениях, противоположных действию внешней нагрузки. 3. Внешний момент никак не влияет на эпюру поперечной силы. 4. Эпюра изгибающего момента на любом участке бруса представляет собой прямую, наклонную к нулевой линии. На участках, где действует только внешний момент, эпюра изгибающего момента представляет собой прямую, параллельную нулевой линии. 5. Изгибающий момент в любой характерной точке равен алгебраической сумме моментов относительно этой точки внешней нагрузки, действующей слева или справа от неё. Причём, если в характерной точке нет внешнего момента, достаточно определить алгебраическую сумму моментов внешней нагрузки относительно её или слева, или справа. Если же в характерной точке действует внешний момент, то надо определять алгебраическую сумму моментов внешней нагрузки относительно её и слева и справа. Сила, действующая вверх, даёт положительный момент относительно характерной точки, сила, действующая вниз – отрицательный. Момент, действующий по направлению движения часовой стрелки, будет положительным, а, действующий против направления движения часовой стрелки – отрицательным при построении эпюры слева направо. При построении эпюры справа налево всё наоборот, т. е. момент, действующий в направлении движения часовой стрелки, будет отрицательным, а, действующий против движения часовой стрелки – положительным. Реакции опор балки определены в задании 1.5. пример 3: RB = 10 кН, RD = 22 кН. Строим эпюру поперечной силы, следуя слева направо: QyA = - F1 = - 18 кН, т. к, сила F1 действует вниз. QyB = - F1 + RB = - 18 + 10 = - 8 кН. Скачок на величину RB = 10 кН вверх. QyC = -F1 + RB + F2 = - 18 + 10 + 30 = 22 кН. Скачок на величину F2 = 30 кН вверх. QyD = 22 кН. Строим эпюру изгибающего момента, определив их значения в характерных точках: точка А Внешних моментов нет, и слева от точки А не действует внешняя нагрузка, следовательно, МхА = 0; точка В. Внешних моментов нет, и слева от точки В действует внешняя сила F1, следова- тельно, точка С. Действует внешний момент, следовательно, надо определять изгибающие момен- ты слева и справа от неё:
точка D. Действует внешний момент, следовательно, надо определять изгибающие моменты слева и справа от неё:
По полученным результатам построены эпюры поперечной силы и изгибающего момента (рисунок 56).
Рисунок 56. Расчётная схема, эпюры Qy и Mx Задача для самостоятельного решения. Для расчётной схемы балки, рассчитанной по рисунку 19 построить эпюры поперечной силы и изгибающего момента.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.233 (0.008 с.) |

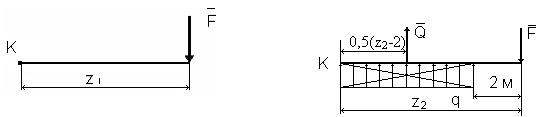
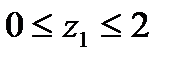 м
м 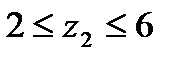 м
м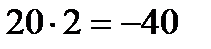 кНм при z2 = 2 м Qy2 = 20 – 0 = 20 кН
кНм при z2 = 2 м Qy2 = 20 – 0 = 20 кН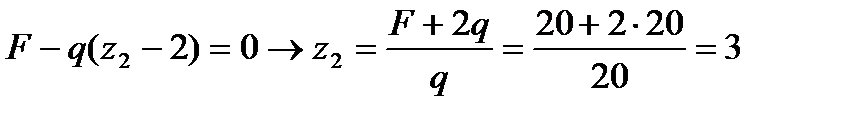 м.
м.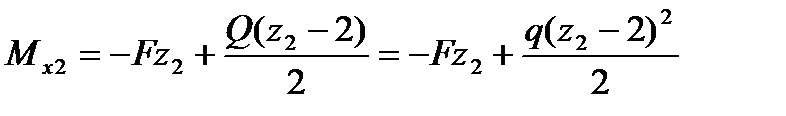 .
.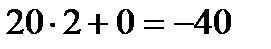 кНм
кНм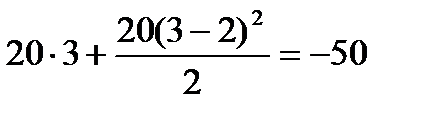 кНм
кНм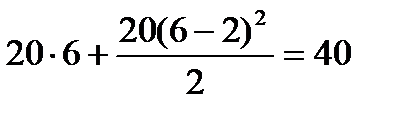 кНм
кНм 3 участок (рисунок 54).
3 участок (рисунок 54).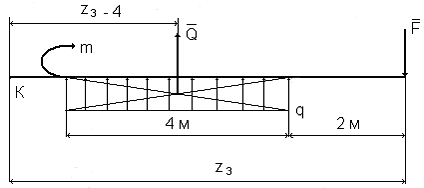
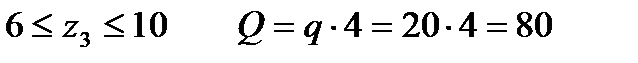 кН
кН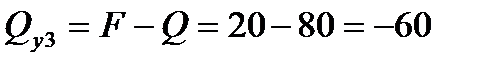 кН.
кН.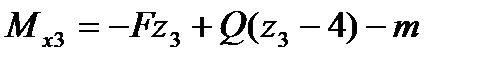
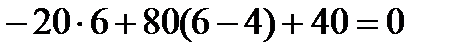
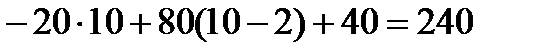 кНм
кНм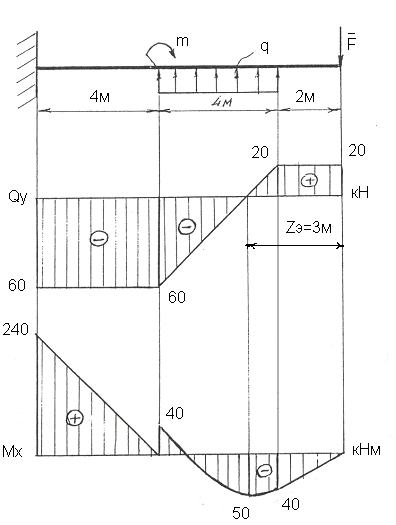
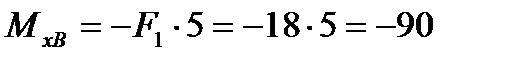 кНм;
кНм;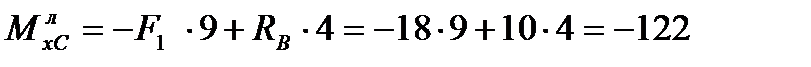 кНм – слева от точки С.
кНм – слева от точки С.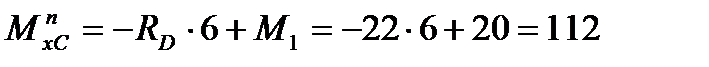 кНм – справа от точки С.
кНм – справа от точки С.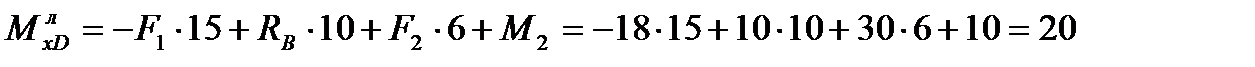 кНм – слева от точки D
кНм – слева от точки D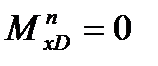 , т. к. справа от точки D нет внешней нагрузки.
, т. к. справа от точки D нет внешней нагрузки.