
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні властивості алгоритмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Багатий досвід розроблення та застосування алгоритмів підказує низку їх загальних властивостей: § дискретність і скінченність алгоритму (результативність); § детермінованість алгоритму (розпізнаваність та однозначна визначеність); § спрямованість алгоритму; § масовість алгоритму (універсальність); § елементарність кроків алгоритму. Дискретність алгоритму. Будь-який алгоритм можна розглядати як процес послідовної побудови величин, що відбувається у дискретному часі за визначеним записом (програмою). У початковий момент задаються вихідні дані, а у кожний наступний момент за програмою одержуємо сукупність наступних величин. Тобто програма йде крок за кроком, незалежно від часу. Детермінованість алгоритму. Визначеність. Сукупність величин, стримуваних у якийсь (не початковий) момент часу, однозначно визначається сукупністю величин, одержаних у попередні моменти часу. Перетворення на кожному кроці повинні бути однозначно визначеними. Спрямованість алгоритму (результативність). Якщо спосіб отримання наступної величини з будь-якої заданої не є результативним, то повинна бути вказівка, що саме потрібно вважати результатом алгоритму. Інакше кажучи, алгоритм через скінченну кількість тактів часу (кроків) повинен привести до зупинення, яке свідчить про досягнення потрібного результату. Тобто якщо при певних вхідних даних алгоритм не може дійти до кінця за скінченну кількість кроків, то цей алгоритм не може дати точного розв’язку задачі. Масовість алгоритму. Алгоритм служить для розв’язування цілого класу задач, при цьому початкова сукупність величин може вибиратися з деякої множини. Наприклад, у алгоритмі Евкліда числа a та b вибираються з нескінченної множини цілих чисел. У математиці проблема вважається розв¢язаною, якщо для неї знайдений загальний алгоритм. Тобто це можливість розв¢язання цілого класу задач, а не якоїсь конкретної. Елементарність кроків алгоритму. Запис про одержання наступної сукупності величин із попередньої має бути простим і локальним. Це означає, що відповідна операція повинна бути елементарною для виконання алгоритму (чи людиною, чи машиною). Приклади алгоритмів. Складність алгоритмів Загальну схему алгоритму можна подати у такому вигляді (рис. 6.3.1):
Рис. 6.3.1. Блок-схема алгоритму Для візуалізації роботи алгоритму можна використовувати блок-схеми. Елементи блок-схеми:
Приклад 1 Скласти алгоритм і зобразити за допомогою блок-схеми розв’язання квадратного рівняння
Рис. 6.3.2. Блок-схема розв’язування квадратного рівняння
1. Визначаємо a, b, c. 2. Обчислюємо детрмінант 3. Детермінант порівнюємо з 0. 4. Якщо D>=0, то рівнянн має два розв¢язки 5. Завершуємо роботу програми. 6. Якщо D < 0, то рівнянн не має розв’язків. 7. Завершуємо роботу програми. 8. Приклад 2 Відсортувати у порядку зростання задану послідовність чисел 3 –1 0 1 8 6 5 -5. Ідея алгоритму:
1) беремо перше число; 2) порівнюємо його за величиною з наступним числом; 3) якщо перше число більше від наступного, то переставляємо ці числа місцями; 4) збільшимо лічильник i на одиницю та переходимо до наступного числа; 5) кроки 2 - 4 повторюємо до тих пір, поки змінна і буде рівною n. Цикл повинен повторюватися n´n разів (n — кількість елементів у масиві). Крім масиву, будемо використовувати додаткову змінну k для перестановки чисел. Перестановку чисел здійснюватимемо таким чином (рис. 6.3.3): k = A[i]; A[i] = A[i+1]; A[i+1] = k.
Рис. 6.3.3. Схема перестановки чисел
Вхідний масив A[1] …A[n] – послідовність довжини n, що підлягає сортуванню. Блок-схема алгоритму має такий вигляд (рис. 6.3.4):
Рис. 6.3.4. Блок-схема сортування послідовності чисел Приклад 3. Знайти максимальне число в послідовності чисел. Маємо наступний алгоритм: 1) беремо перше число; 2) нехай вибране перше число є максимальним; 3) кожне число послідовності порівнюємо із цим максимальним числом; 4) як тільки з’явиться число, більше від максимального, то йому надаємо значення максимального числа; 5) переходимо до пункту 3; 6) як тільки максимальне число стане більшим від n, то зупиняємо програму. Крім масиву чисел, використовується змінна max. A[1] …A[n] – послідовність довжини n. Блок-схема має такий вигляд (рис. 6.3.5)
Рис. 6.3.5. Блок-схема знаходження максимального значення послідовності чисел Розглядаючи різні алгоритми розв’язку однієї й тієї ж задачі, слід проаналізувати, скількох обчислювальних ресурсів вони потребують, та вибрати найбільш ефективний алгоритм. Безумовно, ефективність залежить від вибору обчислювальної моделі. Розрізняють складність самого алгоритму і складність його опису (реалізації). Складність опису алгоритму – це величина, що характеризує довжину опису алгоритму. Складність алгоритму (складність обчислення алгоритму) – це функція, що дає числову оцінку тривалості роботи алгоритму з моменту надходження на його вхід початкових даних до моменту одержання алгоритмом вихідних даних. Для оцінювання складності алгоритмів існує багато критеріїв. Найчастіше розглядається оцінка часу повного розв’язку задачі й зростання місткості пам’яті при збільшенні обсягу вхідних даних. Розміром задачі називається число, яке виражає міру кількості вхідних даних. Наприклад, розміром множення матриць може бути найбільший розмір матриць-чинників. Розміром задачі на графі може бути кількість ребер даного графа. Час, котрий витрачає алгоритм, як функція розміру задачі, називається часовою складністю цього алгоритму. Обсяг пам’яті, що використовує алгоритм, як функція розміру задачі, називається місткісною складністю цього алгоритму. При заданих обмеженнях пам’яті та швидкості комп’ютера складність алгоритму визначає, врешті-решт, розмір задач, котрі можна розв’язати за цим алгоритмом. Генетичний алгоритм Генетичний алгоритм – це аналітичні технології, створені та перевірені самою природою за мільйони років її існування. Вони дозволяють розв’язувати задачі прогнозування, класифікації, пошуку оптимальних варіантів, і є незамінні у тих випадках, коли у звичайних умовах розв’язування задачі основано на інтуїції або досвіді, а не на строгому (математичному змісті) її опису. Природний відбір у природі. Еволюційна природа стверджує, що кожний біологічний вид цілеспрямовано розвивається та змінюється для того, щоб найкращим чином пристосуватися до навколишнього середовища. У процесі еволюції багато видів комах, риб дістали захисний колір, людина стала володарем найскладнішої нервової системи. Можна сказати, що еволюція – це процес оптимізації всіх живих організмів. Основний механізм еволюції – це природний добір. Його суть полягає у тому, що найбільш пристосовані особини мають більше можливостей виживання і розмноження, а як наслідок – приносять більше потомства, ніж погано пристосовані особини. При цьому за допомогою передачі генетичної інформації (генетичного наслідування) потомки наслідують від батьків основні їх якості. Таким чином, потомки сильних індивідуумів також відносно добре пристосовані та їх частка у загальній масі буде зростати. Після зміни декількох десятків або сотень поколінь середня пристосованість цього виду значно зростає. Щоб зробити зрозумілими принципи роботи генетичних алгоритмів, пояснимо, як налаштовані механізми генетичного наслідування у природі. У кожній клітині будь-якої тварини міститься вся генетична інформація цієї особини. Вона записана у вигляді набору дуже довгих молекул ДНК. Кожна така молекула – це ланцюг, що складається з молекул нуклеотидів чотирьох типів (A, T, C, G). Інформація несе порядок слідування нуклеотидів у ДНК. У тваринній клітині кожна молекула ДНК оточена оболонкою, таке утворення називається хромосомою. Кожна спадкова якість особини (колір очей, спадкові хвороби, тип волосся, тощо) кодується визначеною частиною хромосом, яка називається геном цієї властивості. При розмноженні тварин відбувається злиття двох батьківських статевих клітин та їх ДНК взаємодіють, утворюючи ДНК потомка. Основний спосіб взаємодії – кросовер (схрещування). При кросовері ДНК предків діляться на дві частини, а потім обмінюються своїми половинками. При наслідуванні можливі мутації через радіоактивність або інші впливи, у результаті яких можуть змінитися деякі гени у статевих клітинах одного з батьків. Змінені гени передаються потомку і дають йому нові властивості. Якщо ці нові властивості корисні, то скоріше за все вони збережуться у певному виді – при цьому відбудеться скачкоподібне підвищення пристосованості виду. Що таке генетичний алгоритм? Нехай дана деяка складна функція (цільова функція), що залежить від декількох змінних, і потрібно знайти такі значення змінних, при яких значення змінних буде максимальним. Задачі такого виду називаються задачами оптимізації й трапляються на практиці доволі часто. Одним з таких прикладів є задача розподілу інвестицій. У цій задачі змінними є обсяги інвестицій у кожний проект, а функцією, яку можна максимізувати, – сумарний дохід інвестора. Також дано значення мінімального та максимального обсягу вкладень у кожний із проектів, котрі задають область зміни кожної із змінних. Спробуємо розв’язати цю задачу, застосовуючи відомий нам природний спосіб оптимізації. Будемо розглядати кожний варіант інвестування (набір значень змінних) як індивідуума, а дохідність цього варіанта – як пристосованість цього індивідуума. Тоді у процесі еволюції (якщо ми зможемо це організувати) пристосованість індивідуумів буде зростати, а значить, будуть з’являтися все бльш і більш дохідні варіанти інвестування. Спинивши еволюцію у деякий момент та вибравши найкращого індивідуума, ми отримаємо достатньо оптимальний розв’язок задачі. Генетичний алгоритм – це проста модель еволюції у природі, реалізована у вигляді комп’ютерної програми. У ній використовується як аналог механізму генетичного наслідування, так і аналог природного відбору. При цьому зберігається біологічна термінологія в спрощеному вигляді (табл. 6.4.1). Моделювання генетичного наслідування Таблиця 6.4.1
Щоб змоделювати еволюційний процес, згенеруємо спочатку випадкову популяцію – декілька індивідуумів з випадковим набором хромосом (числовий вектор). Генетичний алгоритм імітує еволюцію цієї популяції як циклічний процес схрещування індивідуумів та зміни поколінь. Життєвий цикл популяції – це процес формування нової популяції із старої, після чого стара популяція гине. Після відбору до нової популяції знову застосовується операція кросовера й мутації, потім знову відбувається відбір і т. д. Відбір у генетичному алгоритмі тісно пов’язаний з принципами природного відбору наступним чином (табл. 6.4.2):
Зв’язок генетичного алгоритму з природним відбором Таблиця 6.4.2
Таким чином, модель відбору визначається, яким чином потрібно будувати популяцію наступного покоління. Як правило, вірогідність участі індивідуума у схрещуванні береться пропорціональною до його пристосованості. Часто використовується так звана стратегія елітизму, при котрій декілька найкращих індивідуумів переходять у наступне покоління без змін, не беручи участі у кросоверзі та відборі. В будь-якому випадку кожне наступне покоління буде у середньому краще від попереднього. Коли пристосованість індивідуумів перестає помітно збільшуватися, процес спиняють і у як розв’язок беруть найкращий зі знайдених індивідуумів. Повертаючись до задачі оптимального розподілу інвестицій, пояснимо особливості реалізації генетичного алгоритму в цьому випадку. Індивідуум = варіант розв’язку задачі = набір із 10 хромосом Хромосома Оскільки обсяги вкладень обмежені, не всі значення хромосом є допустимими. Це враховується при генерації популяції. Оскільки сумарний обсяг інвестицій фіксований, то реально варіюють лише 9 хромосом, а значення 10-ї визначається за ними однозначно.
Генетичний алгоритм 1. Створення структури розв’язку шуканої задачі у вигляді масиву a[i], i=1,…n, де n- максимальне число компонент структури. Приклад: пошук функції 2. Створення показника ефективності структури, заповненої конкретними значеннями. Приклад: показником ефективності для нашого прикладу буде нев’язка, визначена методом найменших квадратів. 3. Задання деякого масиву різних структур 4. Розрахунок показників ефективності 5. Природний добір структур за деяким правилом вибору найкращих структур серед заданого масива структур. Приклад: можна за правилом 6. Заміна вибувлих структур на нові, народжені від найбільш пристосованих структур за допомогою генетичних операторів: А) Мутація-заміна у структурі одного із значень випадково вибраної компоненти. Приклад: із Б) Інверсія-перестановка в структурі деякої її частини навпаки. Приклад: із В) Кросинговер – створення структури, основаної на двох структурах – заміною однієї частини першої структури на ту ж область у другій. Приклад: із (A, B, C, D, E) та (a, b, c, d, e) отримаємо (A, B, c, d, E). 7. Переходимо до етапу 4.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 743; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.136 (0.008 с.) |



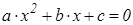 (рис. 6.3.2).
(рис. 6.3.2).
 .
. .
.


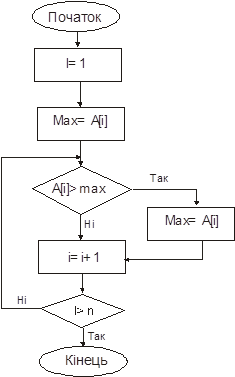

 найкращого у класі поліномів наближення експериментальних точок
найкращого у класі поліномів наближення експериментальних точок  . Структура визначається бітовим масивом, де кожному елементу масиву зіставлений найпростіший многочлен типу
. Структура визначається бітовим масивом, де кожному елементу масиву зіставлений найпростіший многочлен типу 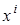 ,
,  , де n – максимальний степінь полінома.
, де n – максимальний степінь полінома. , де
, де  , де
, де 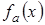 є сума всіх елементів виду
є сума всіх елементів виду  , де
, де  або 1.
або 1. ,
,  , розмірністю
, розмірністю 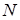 , більшою, ніж число компонент n у структурі. Цей масив можна згенерувати випадковим чином, задавши 0 та 1 у кожній структурі.
, більшою, ніж число компонент n у структурі. Цей масив можна згенерувати випадковим чином, задавши 0 та 1 у кожній структурі. для кожної структури
для кожної структури  – середнє значення
– середнє значення  , то структура залишається, інакше вмирає. Якщо різниця між попереднім
, то структура залишається, інакше вмирає. Якщо різниця між попереднім  та новим
та новим  отримаємо
отримаємо  .
.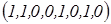 .
.


