
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні характеристики нечітких множин
Нехай § Величина § Нечітка множина є пустою, якщо § Нечітка множина є унімодальною, якщо § Носієм нечіткої множини А є звичайна підмножина із властивістю § Елементи Приклади нечітких множин 1. Нехай E={0,1,2,..,10}, M=[0,1]. Нечітку множину “декілька” можна визначити таким чином: “декілька” = 0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8; її характеристики: висота = 1, носій = {3,4,5,6,7,8}, точки переходу — {3,8}. 2. Нехай E = {0,1,2,3,...,n,...}. Нечітку множину “малий” можна визначити так:
3. Нехай E = {1,2,3,...,100}, відповідає поняттю “вік”. Тоді нечітку множину “молодий” можна визначити за допомогою виразу
Нечітка множина “молодий” на універсальній множині E' ={Іванов, Петров, Сидоров,...} задається за допомогою функції належності 4. Нехай E = {Запорожець, Жигулі, Мерседес,....} – множина марок автомобілів, а E' = [0,µ] – універсальна множина “вартість”, тоді на E' ми можемо визначити нечіткі множини типу: “для бідних”, “для середнього класу”, “престижні” з функціями належності типу (рис. 1.5.3):
Рис. 1.5.3. Графічне зображення нечітких множин Маючи ці функції й знаючи ціну автомобілей із E у цей момент часу, визначимо на E' нечіткі множини з цими назвами. Так, нечітка множина “для небагатих”, задана на універсальній множині E={Запорожець, Жигулі, Мерседес,....} виглядає наступним чином (рис. 1.5.4):
Рис. 1.5.4. Графічне зображення нечітких множин Аналогічно можна визначити нечітку множину “швидкісні”, “середні”, “тихохідні” і т.д. Методи побудови функції належності нечітких множин У приведених вище прикладах використані прямі методи, коли експерт або просто задає для будь-якого
У багатьох задачах при характеристиці об’єкта можна виділити набір ознак і для будь-якого з них визначити полярні значення, що відповідають значенням функції належності, 0 або 1. Наприклад, у задачі розпізнання обличчя можна виділити наступні пункти:
Продовження
Для конкретного обличчя А експерт, виходячи із наведеної шкали, задає
Непрямі методи визначення значень функції належності використовуються у випадках, коли немає елементарних вимірних властивостей для визначення нечіткої множини. Як правило, це методи попарних порівнянь. Якщо б значення функцій належності були відомі, наприклад, Операції над нечіткими множинами
Нехай А і В – нечіткі множини на універсальній множині Е. Говорять, що А міститься у В, якщо Іноді використовують термін “домінування”, тобто у випадку якщо Рівність. А і В рівні, тобто Доповнення. Нехай Очевидно, що Перетин. Об’єднання. Різниця.
Диз’юнктивна сума. Приклад. Нехай дано множини: A = 0,4/ x1 + 0,2/ x2+0/ x3+1/ x4; B = 0,7/ x1+0,9/ x2+0,1/ x3+1/ x4;
C = 0,1/ x1+1/ x2+0,2/ x3+0,9/ x4. 1. 2.
3. 4. 5.
6. Наочне представлення операцій над нечіткими множинами Для нечітких множин можна застосувати візуальне представлення. Розглянемо прямокутну систему координат, на осі ординат якої відкладаються значення Нехай А нечіткий інтервал між 5 та 8 і В нечітке число 4, як показано на рисунку 1.5.5.
Рис. 1.5.5. Графічне зображення нечітких множин А та В На рисунку 1.2.14 проілюструємо нечітку множину між 5 та 8 І (ЕND) біля 4 (синя лінія).
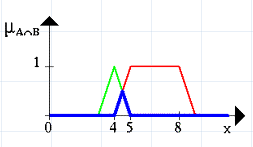
Рис. 1.5.6. Графічне зображення операції перетину нечітких множин А та В Нечітка множина між 5 та 8 АБО (OR) показано на наступному рисунку 1.5.7 (знову синя лінія).
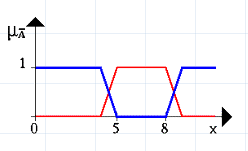
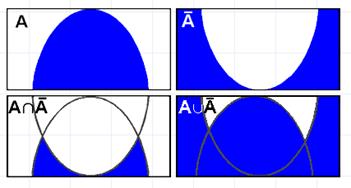
Рис. 1.5.7. Графічне зображення операції об’єднання нечітких множин А та В Наступний рисунок 1.5.8 ілюструє операцію заперечення. Виділена лінія – це заперечення нечіткої множини А.
Рис. 1.5.8. Геометричне зображення операції заперечення На цьому рисунку заштрихована частина відповідає нечіткій множині А та зображає область значень А і всіх нечітких множин, що містяться в А. Останній рисунок 1.5.9 зображає відповідно
Рис. 1.5.9. Операції
Властивості операцій Комутативний закон для об’єднання і перетину множин А È В= В È А; А Ç В= В Ç А. Асоціативний закон для об’єднання і перетину множин А È (В È С)=(А È В) È С; А Ç (В Ç С)=(А Ç В) Ç С. Дистрибутивний закон для об’єднання й перетину множин А È (В Ç С)=(А È В) Ç(А È С); А Ç (В È С)=(А Ç В) È(А Ç С). Властивості пустої множини та універсума відносно об’єднання А ÈÆ = А; А ÇÆ = Æ; А È Е = Е; А Ç Е = А; Закон ідемпотентност ідля об’єднання і перетину множин А È А = А; А Ç А = А. Закон інволюції
Теорема де Моргана
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 727; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.131.178 (0.019 с.) |
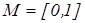 та А – нечітка множина з елементами з універсальної множини Е і множиною належностей М.
та А – нечітка множина з елементами з універсальної множини Е і множиною належностей М. (верхня границя) називається висотою нечіткої множини А. Нечітка множина А є нормальною, якщо її висота дорівнює 1, тобто верхня границя її функції належності дорівнює 1 (
(верхня границя) називається висотою нечіткої множини А. Нечітка множина А є нормальною, якщо її висота дорівнює 1, тобто верхня границя її функції належності дорівнює 1 (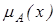 <1 нечітка множина називається субнормальною.
<1 нечітка множина називається субнормальною.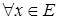
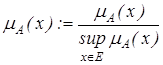 .
.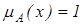 лише для одного x із Е.
лише для одного x із Е.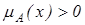 , тобто
, тобто 
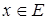 , для яких
, для яких  називаються точками переходу множини А.
називаються точками переходу множини А.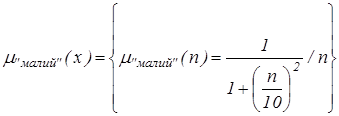 .
. .
. на множині E = {1,2,3,..100} (вік), що називається відносно E' функцією сумісності, при цьому
на множині E = {1,2,3,..100} (вік), що називається відносно E' функцією сумісності, при цьому 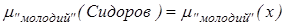 , де
, де  – вік Сидорова.
– вік Сидорова.

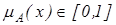 , формуючи векторну функцію належності
, формуючи векторну функцію належності .
.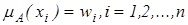 , тоді попарні порівняння можна представити матрицею відношень
, тоді попарні порівняння можна представити матрицею відношень 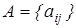 , де
, де 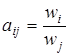 (операція ділення).
(операція ділення).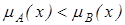 . Позначення:
. Позначення: 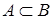 .
. . Позначення:
. Позначення:  .
.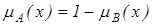 . Позначення:
. Позначення:  або
або 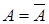 .
.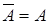 (доповнення визначене для
(доповнення визначене для 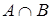 – найбільш нечітка підмножина, яка міститься одночасно в А і В.
– найбільш нечітка підмножина, яка міститься одночасно в А і В.  .
.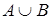 – найменша нечітка підмножина, котра включає як А, так і В, з функцією належності.
– найменша нечітка підмножина, котра включає як А, так і В, з функцією належності.  .
.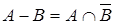 З функцією належності
З функцією належності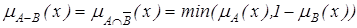 .
.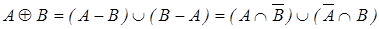 з функцією належності:
з функцією належності: 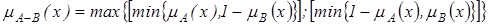
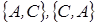 – пари недомінуючих множин.
– пари недомінуючих множин.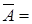 0,6/ x1 + 0,8/x2 + 1/x3 + 0/x4;
0,6/ x1 + 0,8/x2 + 1/x3 + 0/x4;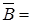 0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4.
0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4.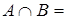 0,4/x1 + 0,2/x2 + 0/x3 + 1/x4.
0,4/x1 + 0,2/x2 + 0/x3 + 1/x4.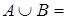 0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4.
0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4. 0,3/x1 + 0,1/x2 + 0/x3 + 0/x4;
0,3/x1 + 0,1/x2 + 0/x3 + 0/x4;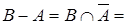 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.
0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.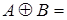 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.
0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.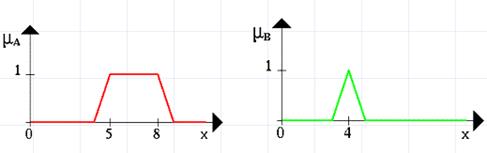

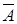 ,
,  ,
, 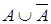 .
.
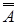 =А
=А ;
; .
.


