
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення впорядкованої пари та декартового добуткуСодержание книги
Поиск на нашем сайте
Багато задач математики, техніки й інших сфер людської діяльності дістають зручну інтерпретацію мовою теорії відношень. Усі арифметичні операції – по суті відношення між числовими множинами. Множина деталей залишається складським майном, доки між ними не реалізуються певні відношення, які перетворюють ці деталі в якийсь механізм або прилад (телевізор, верстат, будинок, міст та ін.). Відношення застосовують в побудові комп’ютерних баз, які організовані у вигляді таблиць даних, а також застосовуються у програмуванні. Різноманітні відошення складаються між людьми – батьки, діти, начальники, вчителі, учні. Самі дані обробляються і перетворюються за допомогою операцій, математично точно визначених для відношень. Останні реалізують у математичних термінах на абстрактних множинах реальні зв’язки між реальними об’єктами. Для формального опису всіляких комбінацій з елементів множин, що входять до відношення, використовується поняття декартового добутку множин. Нехай маємо множини Приклад 1 A={a1,a2,a3,a4}, B={b1,b2}, тоді А ´ В = {a1,b1},{a1,b2},{a2,b1},{a2,b2},{a3,b1},{a3,b2},{a4,b1},{a4,b2}. Приклад 2 A={a1,a2}, тоді A3={(a1,a1,a1),(a1,a1,a2),(a1,a2,a1,),(a1,a2,a2), (a2,a1,a1),(a2,a1,a2),(a2,a2,a1,),(a2,a2,a2)}. Порядок пар може бути довільним, але розміщення елементів у кожній парі визначається порядком множин, що перемножуються, тому А x В¹ В x А. N-арне відношення R на множині Добуток множин не підлягає асоціативному та комутативному законам, але для нього виконується закон дистрибутивності відносно операцій об’єднання перетину та різниці:
Примітка. У результаті операцій об’єднання, перетину тощо завжди одержуємо множину, елементи котрої (якщо вона не пуста) належать вихідним множинам. Елементи добутку множин суттєво відрізняються від елементів співмножників і являють собою об’єкти іншої категорії. Нехай N – множина натуральних чисел. Тоді N x N буде множиною пар натуральних чисел (p,q), кожна з котрих визначає найрізноманітніші об¢єкти: дроби p/q, суми p+q номери будинків і квартир, пари учасників шахового турніру. При цьому (p,q)¹(q,p). Якщо n=1, то таке відношення називається унарним, n=2 – бінарним, n=3 – тернарним.
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.43.244 (0.007 с.) |

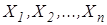 . Декартовим добутком (добутком множин)
. Декартовим добутком (добутком множин)  називається множина всіх упорядкованих наборів
називається множина всіх упорядкованих наборів  з n елементів (що називаються кортежами довжини n), із яких перший елемент належить множині
з n елементів (що називаються кортежами довжини n), із яких перший елемент належить множині  , а другий – множині
, а другий – множині  , n-й –
, n-й – 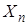 . Декартів добуток
. Декартів добуток  , у котрому одна й та ж множина
, у котрому одна й та ж множина  помножується n разів сама на себе, називається декартовим степенем множини і позначається
помножується n разів сама на себе, називається декартовим степенем множини і позначається 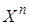 .
. .
.



