
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальна характеристика автоматів
У техніці з поняттям автомата, як правило, пов’язують деякий прилад, здатний виконувати визначені функції без утручання людини або з її обмеженою участю. Однак таке поняття є дуже вузьким. У широкому розумінні кінцевий автомат – це математична модель, що відображає фізичні та абстрактні явища найрізноманітнішої природи. Така модель успішно використовується як у техніці (проектування обчислювальних машин, систем управління й зв¢язку), так і в інших галузях – психології та фізіології (дослідження діяльності нервової системи людини і найпростіших видів поведінки тварин), лінгвістиці (аналіз синтаксису різних мов, розшифрування стародавніх рукописів), теорії та практиці адміністративного управління. Автомат – це схематизований алгоритм. Обчислення за алгоритмом можна розглядати як деякий процес, котрий описується своєю множиною станів, початковим станом і правилами переходу від стану до стану. Універсальність теорії автоматів дозволяє розглядати з єдиної точки зору різні об’єкти, встановлювати зв’язки й аналоги між ними переносити результати з однієї області в іншу. Автомат можна зобразити у вигляді схеми (рис. 5.1.1).
Рис. 5.1.1. Схема автомата Автомат складається з трьох частин: вхідної стрічки, керуючого пристрою зі скінченною пам’яттю і допоміжної або робочої пам’яті. Вхідну стрічку можна розглядати як лінійну послідовність клітинок, чи комірок, причому кожна комірка містить точно один вхідний символ із деякого скінченного вхідного алфавіту. Ліву і праву комірки можуть займати особливі кінцеві маркери, позначимо їх l. Порожні комірки позначаємо e. За допомогою вхідної стрічки зображується інформація, що надходить на вхід автомата. Вхідна головка у кожний момент читає одну вхідну комірку. За один крок роботи автомата вхідна головка може зміститися на одну комірку вліво, залишитися нерухомою або зміститися на одну комірку вправо. Автомат, який ніколи не переміщує свою вхідну головку вліво, називається одностороннім. Схему вхідної стрічки та вхідної головки зображено на рисунку 5.1.2. Вхідна головка може бути тільки такою, котра читає, якщо під час роботи автомат не утворює рядок – результат. Існують такі автомати, вхідна головка котрих виконує функції читання і написання. Такі автомати можуть записувати результуючий рядок чи змінювати символи на вхідній стрічці.
Рис. 5.1.2. Вхідна стрічка та вхідна головка Пам’ять автомата – це структура, в якій записуються, зберігаються і зчитуються додаткові дані, що використовуються автоматом при роботі. Для кожного виду автоматів строго визначено тип пам¢яті, функції доступу до пам’яті та перетворення пам’яті. Автомат може не мати пам’яті. Тип пам’яті часто визначає назву автомата. Робота автомата складається з послідовності тактів. Кожний такт складається з послідовності таких дій: 1. Читається поточний вхідний символ. 2. За допомогою функції доступу досліджується пам¢ять, і до неї заноситься деяка інформація. 3. Змінюється стан керуючого пристрою. 4. Записується вихідна інформація у комірки вхідної стрічки. 5. Вхідна головка зміщується на одну комірку вліво, вправо або зберігається у початковому стані. Поточний вхідний символ та інформація, витягнута з пам’яті, разом з поточним станом керуючого пристрою визначають, яким повинен бути цей стан. Таким чином, на кожному такті встановлюється поточна конфігурація автомата, до якої входять: - поточний стан керуючого пристрою; - поточний зміст вхідної стрічки; - поточний зміст робочої пам’яті. Конфігурація автомата змінюється на кожному такті під впливом керуючого пристрою. Керуючий пристрій складається зі скінченної множини станів Автомат починає роботу з початкової конфігурації. При початковій конфігурації керуючий пристрій знаходиться в заданому початковому стані, вхідна голівка оглядає лівий символ на вхідній стрічці, й пам’ять має заздалегідь установлений початковий зміст. Конфігурація, при якій автомат припиняє роботу, називається завершальною. Автомат припиняє роботу, перейшовши в один із станів заздалегідь виділеної множини завершальних станів, або тоді, коли перегляд вхідних даних завершальною. Умови припинення роботи чітко визначаються для кожного конкретного автомата.
Керуючий пристрій є не детермінованим, якщо для кожної конфігурації існує скінченна множина можливих конфігурацій (більше від однієї), так що в будь-яку з них автомат може перейти на наступному кроці. Керуючий пристрій називається детермінованим, якщо для кожної конфігурації існує не більше від однієї можливої наступної конфігурації. Відповідно автомат називається детермінованим і недетермінованим залежно від виду керуючого пристрою. Скінченні автомати Скінченний автомат складається тільки з вхідної стрічки та керуючого пристрою зі скінченною пам’яттю. Кількість його станів скінченне. Керуючий пристрій може бути детермінованим або недетермінованим, але вхідна головка – одностороння, що зміщується вправо. Скінченний автомат – це структура виду M = (X, Y, S, f, g, F), котра визначається як система із скінченною множиною вхідних символів (сигналів) X={x1, x2, x3,…, xp}, із скінченною множиною вихідних символів Y={y1, y2, y3…, yq}, скінченною множиною станів S = {s1, s2, s3,…, sr} та двома характеристичними функціями:
f – відображення множини g – відображення множини
n – номер такту. Функції (d, l) задають деякі відношення між елементами цих множин (рис. 6.2.1).
Рис. 5.2.1. Блок-схема скінченного автомата Відповідно кінцевий автомат можна позначити M = (X, Y, S, d, l). У двійковому структурному алфавіті p = 2n, q = 2m, r = 2k. Загальна блок-схема кінцевого автомата може бути подана у вигляді комбінаційної схеми, що реалізує функції d, l та пам’яті, яка зберігає на один такт попередній стан автомата (рис. 5.2.2).
Рис. 5.2.2. Блок-схема скінченного автомата Ці функції можна розглядати як деяке відображення множини X´ S (чи його підмножини D Ì X ´ S) відповідно на множини X та Y. Якщо X ´ S ® S і X´ S ® Y – автомат називається повним; X´ S ® S – називається повним по переходах. Якщо функції d, l визначені не для всіх наборів із множини X´ S – автомат називається неповним або частково визначеним. Ясно, що послідовні схеми повинні мати здатність зберігати попередній стан до наступного такту, такі автомати називають автоматами з пам’яттю чи послідовними машинами. Як пам’ять можуть бути використані елементи затримки, на виходах котрих повторюються вхідні впливи із зсувом у часі на інтервал між тактами Dt. Інтервал між тактами може бути різним. Широко застосовуються також різні запам’ятовуючі елементи, наприклад тригери, здатні зберігати стани на виходах до тих пір, поки він не змінюється у результаті дії на їх входи. Такі види автоматів називаються дискретними.
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.244.201 (0.021 с.) |


 і відображень, які залежно від попередньої конфігурації дозволяють визначити нову конфігурацію автомата, напрям переміщення вхідної головки (якщо вона не одностороння), інформацію на друку (якщо в автоматі передбачено функцію друку), інформацію, що заносять у пам’ять та витягують із пам’яті (якщо автомат має робочу пам’ять).
і відображень, які залежно від попередньої конфігурації дозволяють визначити нову конфігурацію автомата, напрям переміщення вхідної головки (якщо вона не одностороння), інформацію на друку (якщо в автоматі передбачено функцію друку), інформацію, що заносять у пам’ять та витягують із пам’яті (якщо автомат має робочу пам’ять).
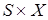 у множину
у множину  , що визначає вибір наступного стану;
, що визначає вибір наступного стану; , що встановлює вихідний символ;
, що встановлює вихідний символ; – множина завершальних станів;
– множина завершальних станів;




