
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості бінарних відношеньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай А – бінарне відношення у множині X. Визначимо основні властивості таких відношень, які повинні виконуватися для всіх (xi, xj)ÎA. Говорять, що AÌX´X: 1. Рефлексивність Бінарне відношення А називається рефлексивним, якщо AÉE (E – тотожне відношення), тобто воно завжди виконується між об¢єктом і ним самим: XAx. Приклад: рівність, самообслуговування. 2. Антирефлексивність Бінарне відношення А називається антирефлексивним, якщо AÇE=Æ, тобто може виконуватися лише для об’єктів, що не співпадають: із xiAxj слідує, що xi¹xj. Приклад: “x є брат y”, але не можна сказати, що x є сам собі брат; строга нерівність, ¢¢бути старшим¢¢. 3. Симетричність Бінарне відношення А називається симетричним, якщо А=А-1, тобто при виконанні xiAxj Þ xjAxi. Приклад: відстань між двома точками, “бути братом”. 4. Антисиметричність Бінарне відношення А називається антисиметричним, якщо АÇА-1ÌE, тобто відношення xiAxj та xjAxi виконуються одночасно тоді й тільки тоді, коли xi=xj. Приклад: нестрога нерівність £, включення. 5. Транзитивність Бінарне відношення АÌА називається транзитивним, якщо АÌА, тобто з xAxj та xjAxkÞ xiAxk виконується умова (“бути дільником”, “бути родичем”). 6. Еквівалентність Бінарне відношення, яке одночасно є рефлексивним, симетричним, транзитивним. Функціональні відношення Функціональна залежність між змінними, або функція, є частковим випадком відношення. Відношення Матриця функціонального відношення, що задане на скінченних множинах X та Y, містить не більше відоднієї одиниці в кожному рядку. Якщо функціональне відношення задано у вигляді графа, то з кожної вершини, котра зображує першу координату, виходить не більше від однієї дуги.
а) функціональне б) функціональне в) нефункціональне Рис. 4.4.1. Приклади функціонального і нефункціонального відношень Нехай Графіком функції (відображення) називається сукупність точок Існує декілька видів відображень, а саме: сюр¢єктивне, ін¢єктивне, бієктивне. Функція
Рис. 4.4.2. Приклад сюр’єктивного відображення Функція
Рис. 4.4.3. Приклад ін’єктивного відображення Функція
Рис. 4.4.4. Приклад бієктивного відображення Нечіткі відношення Нехай Використаємо наступні символи: Так, запис Першу проекцію нечіткого відношення Друга проекція першої проекції (або навпаки) називається глобальною проекцією нечіткого відношення і позначається Якщо Нехай Об’єднання двох відношень
Якщо Перетин двох відношень
Нехай
Контрольні запитання 1. Як пов¢язані теорія відношень та теорія множин? 2. Що називається відношенням? Назвіть способи задавання відношення. 3. Що являє тотожне відношення, повне відношення, порожнє відношення? 4. Як одержати граф відношення, оберненого до даного? 5. Чи може відношення мати не одну, а кілька властивостей? 6. Дати визначення несіткого відношення. 7. Що являє собою перша та друга, глобальна проекції нечіткого відношення? 8. Що являє собою об’єднання двох нечітких відношень?
Лекція 5 Синтез систем на основі поняття про теорію автоматів 1. Загальна характеристика автоматів. 2. Скінченні автомати. 3. Представлення скінченних автоматів. 4. Аналіз кінцевих автоматів. 5. Автомати Мілі та Мура.
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |

 між множинами X та Y (
між множинами X та Y ( ) є функціональним, якщо всі його елементи (впорядковані пари) різні за першим елементом: кожному
) є функціональним, якщо всі його елементи (впорядковані пари) різні за першим елементом: кожному  або відповідає тільки один елемент
або відповідає тільки один елемент  , такий, що
, такий, що  , або такого елемента
, або такого елемента  взагалі не існує.
взагалі не існує.
 – функціональне відношення,
– функціональне відношення,  . Відповідність
. Відповідність  від першого до другого елемента кожної пари
від першого до другого елемента кожної пари  відношення
відношення  , або відображенням
, або відображенням  виду
виду  у декартовому добуткові
у декартовому добуткові  .
.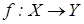 називається сюр’єктивним відображенням, якщо
називається сюр’єктивним відображенням, якщо  . На графі, який зображує сюр’єктивне відображення,з будь-якої вершини
. На графі, який зображує сюр’єктивне відображення,з будь-якої вершини  , заходить не менше від однієї дуги (рис 4.4.2).
, заходить не менше від однієї дуги (рис 4.4.2).
 виходить
виходить  . На графі, що зображує ін’єктивне відображення, з будь-якої вершини
. На графі, що зображує ін’єктивне відображення, з будь-якої вершини 

 – прямий добуток
– прямий добуток  множин та
множин та  – його множина належності; нечітке
– його множина належності; нечітке  запишеться як
запишеться як 
 – позначення максимуму відносно елемента або змінної
– позначення максимуму відносно елемента або змінної  ;
; 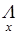 – позначення мінімуму відносно елемента або змінної
– позначення мінімуму відносно елемента або змінної  еквівалентний
еквівалентний  . Запис
. Запис  еквівалентний
еквівалентний  .
. визначає функція належності
визначає функція належності 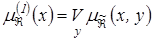 . Аналогічно другу проекцію нечіткого відношення
. Аналогічно другу проекцію нечіткого відношення  .
. . Таким чином,
. Таким чином,  .
. , то говорять, що відношення нормальне. Якщо
, то говорять, що відношення нормальне. Якщо  , то відношення субнормальне.
, то відношення субнормальне. та
та  – два нечітких відношення, такі, що
– два нечітких відношення, такі, що  , тоді говорять, що
, тоді говорять, що  .
. позначається
позначається  або
або  і визначається виразом
і визначається виразом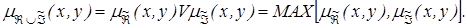
 – відношення, то
– відношення, то  . Результат об’єднання позначається
. Результат об’єднання позначається  або
або  .
. і визначається виразом
і визначається виразом




