
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представлення скінченних автоматів
Автомат може бути заданий різними способами, наприклад, словесним описом його функціонування або переліченням елементів множин X, Y, S з указаним відношенням між ними. В аналізі та синтезі кінцевих автоматів використовують стандартні форми представлення: таблиці, графи, матриці. Елементи множин X, Y, S зручно пронумерувати порядковими числами, починаючи з нуля. Приклад X = {0, 1, 2, 3}; Y = {0, 1}; S = {0, 1, 2, 3}. Представимо функції d, l двома таблицями, рядки яких відповідають станам, а стовпці – входам. Перша таблиця називається таблицею переходів, відповідає функції Друга таблиця називається таблицею виходів, що відповідає функції Таблиця 5.3.1
Таблиця 5.3.2
Таблиця 5.3.3 Загальна таблиця переходів:
Граф автомата будується таким чином: його вершини відповідають станам, а направлені дуги позначаються як диз’юнкція входів, під дією яких здійснюється перехід з одного стану в інший за напрямом дуги. У знаменниках записуємо номери виходів, відповідні цим переходам (рис. 5.3.1).
Рис. 5.3.1. Граф скінченного автомата Оскільки із стану 0 автомат переходить у стан 1, 2, 3, то з вершини 0 графа виходять дуги з вершини 1, 2, 3. При цьому перехід із стану 1 відбувається під дією 2 та йому відповідає вихід 0, тому дуга з вершини 0 в 1 позначається як 2/0. Перехід у стан 2 здійснюється під дією 1, і йому відповідає вихід 0, тому дуга з вершини 0 у 2 помічається як 1/0. Переходи у стан 3 відбуваються під дією 0 та 3, і їм обом відповідає вихід 0, тому дуга з вершини 0 в 3 позначається як диз¢юнкція 0/0Ú3/0. Аналогічно визначаються й інші дуги графа. Петлі відповідають переходам, при яких стан не змінюється. Так цей автомат переходить із стану 2 у 2 під впливом 1 і 2, котрим відповідають виходи 0 та 1. Отже, петля при вершині 2 помічається як диз’юнкція 1/0Ú2/1.
Матриця з’єднання автомата М (або матриця переходів) являє собою квадратну матрицю, у якій номери рядків і стовпців відповідають номерам станів. Клітинка матриці на перетині і -го рядка та j -го стовпця заповнюється диз’юнкцією пар “вхід–вихід”, котра приписана дузі графа, що виходить із і -ї та j -ї вершин. За відсутності такої гілки клітинка заповнюється 0 або залишається пустою. Отже, в нашому випадку маємо (табл. 5.3.4). Таблиця 5.3.4 Матриця з’єднання автомата М
Аналіз скінченних автоматів Повний опис поведінки автоматів полягає у визначенні вихідних сигналів при збудженні його у тактові моменти часу деякою послідовністю вхідних сигналів. Вхідна та вихідна послідовності представляються наборами символів (або їх номерами) із X, Y. Для такого опису необхідно визначати і задавати ще й початковий стан автомата. Найбільш зручно визначати реакцію автомата на вхідну послідовність за його графом. Для цього лише потрібно простежити шлях у графі, починаючи від вершини початкового стану по направленню дуг, які відмічені наступними номерами із вхідної послідовності. Вихідна послідовність визначається номерами, котрими відмічені дуги у порядку їх слідування по пройденому шляху, а послідовність станів автомата – номерами вершин, через які проходить цей шлях. Приклад Нехай маємо початковий стан 0 і вхідну послідовність (2, 0, 1, 1, 2, 3). Тоді визначаємо зміну станів автомата (1, 3, 0, 2, 2, 3) та відповідно вихідну послідовність (0, 1, 0, 0, 1, 1). При початковому стані 2 й при тій же вхідній послідовності одержимо відповідно зміну станів (2, 3, 0, 2, 2, 3) та відповідно вихідну послідовність (1, 1, 0, 0, 1, 1). За допомогою графа автомата легко виділити такі характерні типи його станів: 1) перехідний стан, із котрого можна перейти принаймні в один інший стан, але після цього вже не можна повернутися у нього ні при якій дії (відповідна вершина не має вхідних дуг, але має хоча б одну вихідну дугу);
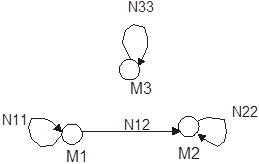
2) тупиковий стан, у котрий можна перейти принаймні з одного до іншого стану, але після цього вже не можна вийти з нього ні при якій дії (відповідна вершина не має вихідних дуг в інші вершини, але має принаймні хоч одну дугу з іншої вершини); 3) ізольований стан, із якого не можна перейти в жодний інший стан і в нього не можна потрапити ні з якого іншого стану (відповідна вершина містить лише петлю). Аналогічні визначення можна дати для деяких сукупностей станів, що розглядаються як підавтомати. Нехай М1, М2, М3 – відповідно перехідний, тупиковий та ізольований підавтомати автомата М, які характеризуються множиною станів S1, S2, S3. Очевидно, виділення таких підавтоматів відповідає розбиттю множини S станів автомата M на неперетинаючі підмножини S1, S2, S3 (рис. 5.4.1). S1È S2È S3 = S; S1Ç S2Ç S3 = Æ.
Рис. 5.4.1. Множина неперетинаючих станів автомата M Матриця відповідного графа може бути представлена у вигляді
Автомати Мілі та Мура Скінчеyнний автомат, у котрому вихідна інформація поставлена у відповідність переходам, називається автоматом Мілі. Скінченний автомат, у якому вихідна інформація поставлена у відповідність станам, називається автоматом Мура. Це означає, що в автоматах Мілі функція виходів – це залежність вихідної інформації від поточного стану і поточної вхідної інформації, а в автоматах Мура функція виходів – це залежність вихідної інформації тільки від поточного стану. Розглянемо приклад автомата Мілі. Приклад 1 Побудувати скінченний автомат, який здійснює додавання двох натуральних чисел, використовуючи їх бінарне зображення. Пояснимо процедуру порозрядного бінарного додавання. Нехай є два числа, записані за допомогою n-розрядного війкового коду:
_____________
Скінченний автомат, що виконує це додавання, можна побудувати, використовуючи тільки два стани. Розглянутий автомат має множину станів Вхідними даними на одному такті є два біти – відповідні біти доданків, тому можливі варіанти вхідної інформації для одного такту – Відображення
Таблиця 5.5.1 Таблиця станів автомата
Продовження таблиці 5.5.1
Діаграму станів, що відповідає цьому автомату, подано на рисунку 5.5.1.
Рис. 5.5.1. Скінченний автомат Мілі для додавання Біля кожної стрілки переходу вказано вхідну інформацію і вихідний сигнал. Наприклад, запис 01.1 біля петлі у стані Приклад 2 Побудувати автомат Мура, який на виході друкує 1, якщо кількість одиниць, прочитаних автоматом у вхідному рядку, ділиться на 3, і друкує 0 у протилежному випадку (автомат також друкує 0, якщо не прочитано жодної одиниці у початковому стані Таблиця 5.5.2 Таблиця станів автомата
Припустимо, на вхід автомата надійшов рядок 0001010100. Розглянемо, яку вихідну інформацію видасть автомат. Побудуємо відповідну таблицю (табл. 5. 5. 3). Після прочитання рядка 0001010100 автомат друкує 1, тобто кількість одиниць, що прочитав автомат у вхідному рядку, ділиться на 3.
Рис. 5.5.2. Автомат Мура Таблиця 5.5.3 Вхідна інформація автомата
Продовження таблиці 5.5.3
Контрольні запитання 1. Для дослідження яких питань використовуються автомати? 2. Поясніть принцип дії та побудову кожної частини автомата. 3. Що включає такт роботи автомата? 4. Чим відрізняються детерміновані й недетерміновані скінченні автомати?
5. Дайте визначення автоматів Мілі та Мура. Лекція 6 Поняття про алгоритм. Роль алгоритмів у системах керування 1. Визначення агоритму, його види. 2. Загальні властивості алгоритму. 3. Приклади алгоритмів. Складність алгоритмів. 4. Генетичний алгоритм.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.22.250 (0.038 с.) |
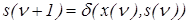 , і її клітинки заповнюються номерами станів
, і її клітинки заповнюються номерами станів  та стану в даний тактовий момент.
та стану в даний тактовий момент. , і її клітинки заповнюються номерами виходів y(n) у той же момент. Наприклад, для заданих X, Y, S такі таблиці можуть мати такий вигляд (табл. 5.3.1, табл. 5.3.2, табл. 5.3.3):
, і її клітинки заповнюються номерами виходів y(n) у той же момент. Наприклад, для заданих X, Y, S такі таблиці можуть мати такий вигляд (табл. 5.3.1, табл. 5.3.2, табл. 5.3.3):
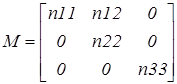 .
. і
і  . Спочатку додаються
. Спочатку додаються 
 та
та  , у результаті чого виходить результат
, у результаті чого виходить результат  та перенесення
та перенесення  . Після цього робиться додавання
. Після цього робиться додавання  ,
,  та
та  й перенесення
й перенесення  . Ця процедура продовжується до кроку n, на якому при додаванні
. Ця процедура продовжується до кроку n, на якому при додаванні  ,
, 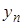 та
та  і виходить
і виходить  та
та  . Остання сума
. Остання сума  дорівнює перенесенню
дорівнює перенесенню 



 Перенесення
Перенесення , множину вхідних символів
, множину вхідних символів  , множину вихідних символів
, множину вихідних символів 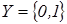 , початковий стан –
, початковий стан –  . Будемо вважати, що автомат припиняє роботу, коли закінчилося надходження вхідних даних. Це означає, що додавання завершено.
. Будемо вважати, що автомат припиняє роботу, коли закінчилося надходження вхідних даних. Це означає, що додавання завершено. . Переходи побудовані відповідно до одержуваної суми, яка зображена вихідним бітом, і перенесенням, котре зображене станом (
. Переходи побудовані відповідно до одержуваної суми, яка зображена вихідним бітом, і перенесенням, котре зображене станом ( – перенесення дорівнює 0,
– перенесення дорівнює 0,  – перенесення дорівнює 1).
– перенесення дорівнює 1). (функція переходів) та
(функція переходів) та 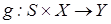 (функція виходів) наведені у таблиці 6.5.1. У таблиці зображено, що коли біти, які додаються, 00 і поточний стан
(функція виходів) наведені у таблиці 6.5.1. У таблиці зображено, що коли біти, які додаються, 00 і поточний стан 


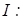

 . Назвемо цей автомат
. Назвемо цей автомат  . Визначимо стани автомата:
. Визначимо стани автомата:  – прочитано кількість одиниць, що дає при діленні на 3 у залишку 2,
– прочитано кількість одиниць, що дає при діленні на 3 у залишку 2,  – прочитано кількість одиниць, кратне 3. Звичайно, що вихідну інформацію у такому автоматі можна поставити у відповідність станам. Побудуємо таблицю переходів (табл. 5.5.2).
– прочитано кількість одиниць, кратне 3. Звичайно, що вихідну інформацію у такому автоматі можна поставити у відповідність станам. Побудуємо таблицю переходів (табл. 5.5.2).




