
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Булева алгебра, тотожні перетворення
Множина всіх булевих функцій разом з операціями заперечення, кон’юнкції, диз’юнкції утворюють булеву алгебру. Справедливі наступні тотожності булевої алгебри: Комутативність x Ú y=y Ú x; x Ù y=y Ù x. Асоціативність x Ú (yÚ z)=(x Ú y)Ú z; x Ù(yÙ z)=(x Ù y)Ù z. Дистрибутивність x Ù(yÚ z)=(x Ù y)Ú (x Ù z); x Ú(yÙ z)=(x Ú y)Ù (x Ú z). Властивість констант x Ú 0= x; x Ù 1= x. Властивість заперечення x Ú xÙ Закони де Моргана
Закони поглинання x Ú (x Ù y) = x Ù (x Ú y)= x. Закони ідемпотентності x Ú x=x Ù x=x, а також тотожності x Ú ( (x Ù y)Ú (x Ù z)Ú (yÙ
Доведемо закон ідемпотентності x Ú x=x Ù x=x; Доведення x Ú x=x Ú x Ù 1=(x Ú x) Ù 1=(x Ú x) Ù (x Ú x Ù x=x Ù x Ú 0= (x Ù x) Ú 0=(x Ù x) Ú (xÙ Доведемо, що x Ú 1= 1. Доведення x Ú 1=x Ú (x Ú Доведемо, що x Ù 0= 0. Доведення x Ù 0= x Ù (x Ú Доведемо закон поглинання x Ú (x Ù y) = x Ù (x Ú y)= x. Доведення x Ú (x Ù y) =(x Ù 1)Ú (x Ù y) = xÙ (1 Ú y)= xÙ 1=x; x Ù (x Ú y)= (x Ú 0)Ù (x Ú y)= x Ú (0Ù y)= x Ú (yÙ 0)= x Ú 0 =x. Доведемо, що Доведення x Ú Доведемо закони де Моргана Доведення На основі властивостей заперечення рівності функцій (x Ú y)Ú( = ((x Ú y)Ú (xÚy)Ù( Отже, співвідношення
Висловлення. Предикати Нехай x1 і x2 — деякі висловлювання, які можуть бути істинними (1) або хибними (0). Наприклад, “Я піду до театру” (x1) та “Я зустріну друга” (x2). Диз’юнкцією є складне висловлення (x1Ú x2) “Я піду до театру або зустріну друга”, а кон’юнкцією (x1Ù x2) “Я піду до театру й зустріну друга”. Зрозуміло: якщо висловлення істинне, то його заперечення хибне. Складне висловлення, утворене диз’юнкцією двох висловлень, істинне за умови, що істинне хоча б одне з них. Складне висловлення, утворене кон’юнкцією двох істинних висловлень, істинне за умови, якщо обидва висловлення істинні одночасно. Отже, висловлення можна розглядати як двійкові змінні, а зв’язки “не”, “або”, “і”, за допомогою котрих утворюються складні висловлення, - як операції над цими змінними. В алгебрі висловлювань використовують ще дві операції: імплікація x1® x2, що відповідає “якщо, то” (таблиця 2.5.1) Таблиця 2.5.1
x1® x2 та еквіваленція x1» x2, що відповідає “тоді й тільки тоді” (таблиця 2.5.2). Таблиця 3.5.2
x1» x2 У нашому прикладі імплікацією буде висловлення “Якщо я піду до театру, то зустріну друга”, а еквіваленцією - “Я піду до театру тоді й тільки тоді, якщо зустріну друга”. Позначивши буквами прості висловлення, можна представити складні висловлення формулою за допомогою простих зв’язок. Приклад: “Якщо тиск масла на кульку клапана більший, ніж зусилля його пружини (x1), то масло відкриває клапан (x2) і частково перетікає з нагнітальної порожнини у впускну (x3)”. Виразу відповідає формула x1® x2x3. Предикати. Зазвичай висловлення виражають властивості одного або декількох об’єктів. Змістовна частина висловлення визначає властивості сукупності об¢єктів, для яких це висловлення істинне, й називається предикатом. Наприклад, висловлення “Іванов - відмінник” істинне або хибне залежно від оцінок, котрі має цей студент. У той же час предикат “ x – відмінник ” визначає підмножину відмінників на деякій множині студентів (група, курс, факультет). Підставивши замість x прізвища студентів, одержимо множину висловлень. Сукупність істинних висловлень і буде відповідати підмножині відмінників.
Предикат являє собою логічну функцію P(x), котра набуває значення (як і булеві функції) 0 або 1. Але на відміну від булевих функцій, значення аргументу x вибираються з деякої множини М об’єктів (xÎМ). У загальному випадкові така функція може залежати від багатьох аргументів x1, x2,…,xn, що набувають значень з однієї і тієї ж множини або з різних множин. Її записують P(x1, x2,…,xn) та називають n-місним предикатом. Приклад: “ x - парне число”, “ x - компонент ланцюга” – одномісні предикати P(x); “ x брат y ”, “ x менше” - двомісні предикати P(x, y); “ x та y -батьки z ” - тримісний предикат P(x, y, z). Якщо аргументи x1, x2,…,xn замінені конкретними значеннями (об’єктами), то предикат переходить у висловлення, котра розглядається як 0 -місний предикат. Оскільки предикати здатні набувати лише значення 0 та 1, то їх також можна зв’язувати логічними операціями. У результаті одержимо формули, що визначають більш складні предикати. Так, якщо P(x) – “ x - інженер”, а Q(x) – “ x - співробітник нашого відділу”, то P(x)ÙQ(x)=R(x) - одномісний предикат “ x — інженер і співробітник нашого відділу” або “ x – інженер нашого відділу”. Очевидно, якщо P - множина інженерів, а Q – множина співробітників даного відділу, то цей предикат відповідає перетину PÇ Q. Отже, існує тісний зв¢язок між логікою предикатів і операціями над множинами. Двійкова арифметика У позиційній системі числення з основою m будь-яке ціле невід¢ємне число a записується послідовністю різних цифр x1 x2...xn, що означає
Десяткова система числення використовує цифри 1,2,3,…,9. У цій системі число можна записати таким чином: 2907=2×103+9×102+1×10+7×100. Для двійкової системи числення достатньо двох цифр 0 та 1. Послідовність цифр x1 x2...xn є записом двійкового n -розрядного числа Переведення цілих десяткових чисел у двійкові здійснюється послідовним діленням вихідного числа й кожної частки від ділення на два. Одержані при цьому залишки (0 та 1) і записані в зворотному порядку дають заявлення десяткового числа у двійковій системі числення. Приклад 1. 26/2=13/2=6/2=3/2=1/2=0 26 12 6 2 0 01011 2610=110102 Перевірка: 1×24+1×23+0×22+1×21+0×20=16+8+2=26. Дробове число переводиться у двійкову систему методом послідовного множення на 2. При цьому кожного разу після коми двійкового числа записується 0 або 1 відповідно до цілої частини результату множення. Послідовне множення продовжується до тих пір, поки дробова частина не перетвориться в 0 або поки не одержимо потрібну кількість двійкових знаків після коми. Приклад 2. Представимо у двійковій системі число 0,3125. 0,3125´2=,6250´2=,2500´2=,5000´2=,0000. 0101 0,312510=0,01012. Перевірка: 0×2-1+1×2-2+0×2-3+1×2-4=1/4+1/16=5/16=0,3125. Якщо число є змішаним, тобто ціла та дробова частини відрізняються від 0, то вони переводяться в двійкову систему окремо: ціла частина — послідовним діленням, а дробова – послідовним множенням. Арифметичні операції над числами зводяться до операцій складання і множення однорозрядних чисел. У двійковій системі числення множення задається таблицею кон’юнкції
0×0=0; 1×0=0; 0×1=0; 1×1=1. Додавання виконується за правилом 0+0=0; 1+0=0; 0+1=1; 1+1=10 (10 – двійкове число, що відповідає десятковому числу 2). Приклад 3. 41+27=68 відповідно 101001+11011=1000100. Приклад 4. 41×5=205 відповідно 101001´101=11001101. 7.Аналіз систем на основі математичної логіки Нечітка логіка (fuzzy logic) – це математична наука, яка є розширеннямкласичної (бульової) логіки й основана на концепції часткової правди – правди, що знаходиться десь посередині між “і” та “немає”. Творець теоретичних основ нечіткої логіки Лотфи-заде (Lotfi Zaden) неодноразово підкреслював, що теорія нечітких висловлень не повинна трактуватись як самостійна, відособлена галузь знань. У деякому аспекті вона служить методологічним розширенням будь-якої іншої специфічної теорії, отриманої шляхом розмивання (fuzzification) її базисних об’єктів (наприклад, чисел), – їхнім перекладом із дискретного стану в безупинне. У наші дні дослідження проводяться, зокрема в області нечітких обчислень (fuzzy calculations), нечітких диференціальних рівнянь (fuzzy differential equations) та ін. Безпосереднє використання алгоритмів нечіткої логіки в додатках – справа поки досить рідкісна. Втім, очевидною областю впровадження є всілякі експертні системи, у тому числі:– нелінійний контроль за процесами (виробництво);– системи, які самонавчаються, названі також класифікаторами (classifiers), дослідження ризикових і критичних ситуацій. У цій області особливо цінується спроможність системи з нечіткою логікою одночасно вдосконалювати декілька каналів узагальнення правил, що помітно відрізняє цей підхід від систем штучного інтелекту, по черзі охоплюючих одну закономірність за іншою;– розпізнавання образів;– фінансовий аналіз (ринки цінних паперів);– дослідження даних (корпоративні сховища);– удосконалення стратегій керування й координації дій, наприклад складне промислове виробництво. Нечітка логіка застосовується також при створенні систем підтримки прийняття рішень фінансового аналізу.Контрольні запитання 1. Дати поняття булевої змінної. 2. Назвати основні функції двозначної логіки. 3. Назвати основні закони булевої алгебри. 4. Назвати операції в алгебрі висловлень. 5. Дати визначення предиката, навести приклади.
Лекція 3 Синтез систем на основні поняття теорії графів 1. Походження графів. 2. Типи скінченних графів. 3. Орієнтовані графи, зважені графи. 4. Суміжність, інцидентність графів, ізоморфізм графів.
5. Маршрути, цикли графів. 6. Планарність графів. Походження графів Багато задач зводяться до розгляду сукупності об’єктів, суттєві властивості яких описуються зв’язками між ними. Наприклад, дивлячись на карту автомобільних доріг, можна цікавитися лише тим, чи існують зв’язки між деякими населеними пунктами, не звертаючи увагу на конфігурацію доріг, відстані й інші подробиці. При вивченні електричних ланцюгів на перший план може виступати характер з’єднань різних його компонентів: резисторів, конденсаторів, джерел тощо. Органічні молекули утворюють структури, характерними властивостями котрих є зв’язки між атомами. Інтерес можуть викликати різні зв’язки між людьми, подіями, станами і взагалі між будь-якими об’єктами. У подібних випадках зручно розглядати об’єкти точками, так називаними вершинами, а зв’язки між ними – лініями (довільної конфігурації), так називаними ребрами. Множина вершин V, зв’язки між котрими визначаються множиною ребер E, називається графом G=(V,E). Граф G задається множиною точок або вершин x1, x2,….., xn, що й позначаються через V, і множиною ліній чи ребер e1, e2,….., en, які позначаються через E та з’єднують між собою всі або частину цих точок. Отже, граф являє собою пару G=(V, E) множин. Ми завжди будемо мати на увазі, що V
Рис. 3.1.1. Граф на V={1,…,7} з множиною ребер E={{1,2}, {1,5}, {2,5}, {3,4}, {5,7}. Множину вершин графа G позначають як V(G), а множину ребер – як E(G). Кількість вершин графа називають його порядком і записують як |G|, кількість його ребер позначають як ||G||. Графи є обмеженими або не обмеженими відповідно до їх порядку. Граф порядку 0 або 1 називаємо тривіальним. Перша робота щодо графів була опублікована двадцятирічним Леонардом Ейлером у 1736 році, коли він працював у Російській академії наук. Вона містила розв’язок задачі про кенінгсберзькі мости: чи можна здійснити прогулянку таким чином, щоб, вийшовши з будь-якого місця міста, повернутися на нього, пройшовши у точності лише один раз по кожному мосту? За умовою не має значення, як проходить шлях по частинах суші a,b,c,d, на котрих розміщено м. Кенінгсберг, тому їх можна представити вершинами. А так звані зв’язки між цими частинами здійснюються лише через сім мостів, але кожний із них зображується у вигляді ребра, що з’єднує відповідні вершини. У результаті одержуємо граф (рис. 3.1.2).
Рис. 3.1.2. Граф до задачі про кенінгсберзькі мости Ейлер дав заперечну відповідь на поставлене питання. Більше того, він довів, що подібний маршрут існує лише для такого графа, кожна з вершин якого пов’язана з парним числом ребер. Але існує велика кількість задач із застосуванням графів, у яких розглядалися б важливі практичні проблеми, багато з них потребувало тонких математичних методів. Уже у XIX ст. Кірхгоф застосував графи для аналізу електричних ланцюгів, а Келі дослідив важливий клас графів для виявлення і перелічення ізомерів насичених вуглеводів. Однак теорія графів як математична дисципліна сформувалася лише у середині 30-их років XX ст. завдяки роботам таких дослідників, як Кенінг, Понтрягін, Зиков, Візинг. Теорія графів має потужний апарат розв’язання прикладних задач із найрізноманітніших галузей науки й техніки. Наприклад, аналіз та синтез ланцюгів і систем, проектування каналів зв’язку й дослідження процесів передачі інформації, побудова контактних схем і вивчення кінцевих автоматів, планування мереж та їх управління, дослідження операцій, вибір оптимальних маршрутів і потоків у мережах, моделювання нервової системи у живих організмів та багато інших задач. Теорія графів тісно пов’язана з такими розділами математики, як теорія множин, математична логіка, теорія ймовірностей.
Нехай маємо два графи G і G¢. Вважаемо, що Якщо
Рис. 3.1.3. Об’єднання, перетин, різниця графів G та G¢ Якщо Типи скінченних графів Якщо множина вершин графа скінченна, то він називається скінченним графом. Скінченний граф G=(V, E), що містить p вершин і q ребер, називається (p, q) - графом (рис. 3.2.1).
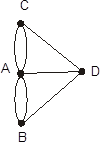
Рис. 3.2.1. Псевдограф (p, q) - графа Нехай V={v1, v2, …vp} та E={e1, e2, …eq} відповідно множина вершин і ребер. Кожне ребро ekÎE й з’єднує пару вершин vi, vj Î V, є його кінцями (граничними вершинами). Для орієнтованого ребра розрізняють початкову вершину, із якої дуга виходить, та кінцеву вершину, куди дуга заходить. Ребро, граничними вершинами котрого є одна й та сама вершина, називається петлею. Ребра з однаковими граничними вершинами є паралельними і називаються кратними. У загальному випадку граф може містити й ізольовані вершини. Наприклад, для (5, 6) (рис. 3.2.1) графа V={v1, v2, v3, v4, v5} E={e1, e2, e3, e4, e5, e6}; e1, e3 –паралельні, e6 – петля, e4 – ізольована вершина. Нехай G=(V,E) є не пустий граф. Множину сусідніх вершин vi у G позначимо як NG(vi) чи коротко через N(vi). Степінь (або валентність) вершини dG(vi)=d(vi) є кількістю |E(vi)| ребер, що виходять із вершини vi. За нашим визначенням графа, це рівнозначне кількості сусідніх вершин. Вершина із степенем 0 є ізольованою. Число Припущення 1. Кількість вершин непарного степеня у графі є завжди парною. Припущення 2. Кожний граф G з одним ребром має підграф H, де Граф без петель і кратних ребер називається простим, або звичайним. Граф без петель, але з кратними ребрами, називають мультиграфом. Найбільш загальний випадок графа, коли допускаються петлі й кратні ребра, називається псевдографом (рис. 3.2.1). Якщо всі вершини графа ізольовані, тобто V={¹Æ} та E={Æ}, то він називається пустим. Простий граф, у якого будь-які дві вершини з’єднані ребром, називається повним. Якщо множина вершин V простого графа допускає таке розбиття на дві неперетинані множини V1 та V2 (V1 Ç V2=Æ), що не існує ребер, які з’єднують вершини однієї й тієї ж підмножини, то вони називаються дводольним, або біграфом (рис. 3.2.2).
а) б) Рис. 3.2.2. Повний граф (а), дводольний граф (б) Орієнтований граф називається простим, якщо він не має строго паралельних дуг та петель. Граф, степені всіх вершин якого однакові та рівні r, називається однорідним (регулярним).
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.213.209 (0.052 с.) |
 =1;
=1;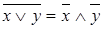 ;
; .
. )=(x Ù z)Ú (yÙ
)=(x Ù z)Ú (yÙ 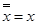 ;
;  ;
;  ; x Ú 1= 1; x Ù 0= 0 та ін.
; x Ú 1= 1; x Ù 0= 0 та ін. .
. =1, за законом комутативності випливає, що
=1, за законом комутативності випливає, що  = 1, маємо x=
= 1, маємо x=  .
. та
та  повинно означати, що
повинно означати, що )=((x Ú
)=((x Ú  доведено. Аналогічно доводиться другий закон. Операції диз’юнктивності й кон’юнктивності задовольняють закони комутативності та асоціативності, тому якщо змінні пов’язані безпосередньо однією із цих операцій, то їх можна виконувати в будь-якому порядку, а формули записувати без дужок. Операцію кон’юнкції часто називають логічним множенням, а операцію диз’юнкції - логічним додаванням. Ще одне спрощення можна допустити, знак кон’юнкції у формулах можна опустити і замість x Ù y писати xy.
доведено. Аналогічно доводиться другий закон. Операції диз’юнктивності й кон’юнктивності задовольняють закони комутативності та асоціативності, тому якщо змінні пов’язані безпосередньо однією із цих операцій, то їх можна виконувати в будь-якому порядку, а формули записувати без дужок. Операцію кон’юнкції часто називають логічним множенням, а операцію диз’юнкції - логічним додаванням. Ще одне спрощення можна допустити, знак кон’юнкції у формулах можна опустити і замість x Ù y писати xy. .
. .
.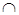 E=ø. Зазвичай, граф являє собою креслення, котре складається з точок (вершин) і ліній (ребер), що з’єднують відповідні дві вершини (рис. 3.1.1).
E=ø. Зазвичай, граф являє собою креслення, котре складається з точок (вершин) і ліній (ребер), що з’єднують відповідні дві вершини (рис. 3.1.1).
 та
та  .
. =Æ, тоді G і G ¢ не перетинаються. Якщо
=Æ, тоді G і G ¢ не перетинаються. Якщо  та
та  , то G¢ є підграфом графа G (граф G – надграфом для G’). У цьому випадкові записуємо
, то G¢ є підграфом графа G (граф G – надграфом для G’). У цьому випадкові записуємо  , формально ми говоримо, що граф G містить граф G¢ (рис. 3.1.3).
, формально ми говоримо, що граф G містить граф G¢ (рис. 3.1.3).
 E x,y
E x,y 
 є мінімальним степенем графа G, а число
є мінімальним степенем графа G, а число  – максимальним степенем. Якщо всі вершини графа G мають один і той самий степінь k, тоді граф G є k -однорідним або просто однорідним. 3-однорідний граф називається кубічним. Число
– максимальним степенем. Якщо всі вершини графа G мають один і той самий степінь k, тоді граф G є k -однорідним або просто однорідним. 3-однорідний граф називається кубічним. Число  – середній степінь графа G. Зрозуміло, що
– середній степінь графа G. Зрозуміло, що 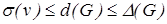 . Середній степінь оцінює глобально те, що локально вимірюється степенями вершин – кількості ребер графа G, що припадає на одну вершину. Іноді дуже зручно виражати це відношення як
. Середній степінь оцінює глобально те, що локально вимірюється степенями вершин – кількості ребер графа G, що припадає на одну вершину. Іноді дуже зручно виражати це відношення як  . Величини d і e звичайно тісно взаємопов’язані. Якщо ми підсумуємо степені всіх вершин у графі G, то врахуємо кожне ребро двічі, по одному разу з кожного кінця. Таким чином,
. Величини d і e звичайно тісно взаємопов’язані. Якщо ми підсумуємо степені всіх вершин у графі G, то врахуємо кожне ребро двічі, по одному разу з кожного кінця. Таким чином,  ,
,  .
.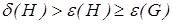 .
.



