Работа сил на наклонной плоскости
Похожие статьи вашей тематики
Пусть требуется поднять на высоту h груз, сила тяжести которого G.

Предположим, что подъем осуществляется тремя способами:
1) Вертикальный
2) По наклонной плоскости с углом подъема α.
3) По менее крутой плоскости с углом подъема β (β<α).
Если считать, что груз перемещается равномерно, то работа по подъеме груза во всех 3-х случаях совершаются одинакова:

Но, в первом случае приходится преодолевать силу тяжести G, во
втором –  , в третьем – , в третьем – 
Так как β<α, то 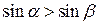 , значит , значит 
Наклонная плоскость, как одно из средств получения выигрыша в силе при перемещении тяжести, широко использование в технике.
Сила F направлена параллельно наклонной плоскости.

При перемещении вверх по наклонной плоскости тела и на него кроме силы F, действует еще три силы:
– сила тяжести G, нормальная реакция наклонной плоскости Rn ,, значение которого равно:

– сила трения Rf, значения которого равно:

При равномерном подъеме тела М четыре силы образуют уравновешенную систему. Алгебраическая сумма работ этих сил равна нулю.

где  – работа силы тяжести – работа силы тяжести
 – работа силы трения – работа силы трения
 – работа нормальной реакции – работа нормальной реакции

Если же требуется определить значение силы F, то с учетом того, что  получаем: получаем:

Полезную часть работы сил F составляют работа по подъему тела на высоту  и тогда: и тогда:

Таким образом КПД наклонной плоскости при подъеме груза силой направленной параллельно наклонной плоскости:


Вывод: КПД наклонной плоскости зависит только от ее угла наклона и коэффициента трения при перемещении груза по плоскости.
Работа и мощность при вращательном движении тел
Допустим, что к рукоятке C колеса, насаженного на ось OZ,

приложена сила  , постоянно направленная перпендикулярно , постоянно направленная перпендикулярно  . При вращении колеса точка приложения силы . При вращении колеса точка приложения силы  перемещается по окружности и элементарная работа этой силы перемещается по окружности и элементарная работа этой силы
 . .
Но так как  , то , то 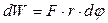 , где произведение , где произведение  называется вращающим моментом. Следовательно, при вращении тела элементарная работа называется вращающим моментом. Следовательно, при вращении тела элементарная работа
 . .
При повороте колеса на угол  работа работа
 . .
Если при этом вращающий момент  , то , то

(работа при вращении тела равна произведению вращающего момента на угол поворота).
Разделив обе части этого равенства на  время действия вращающего момента, получим его мощность: время действия вращающего момента, получим его мощность:
 , ,
или, так как 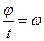 , ,

(мощность при вращении тела равна произведению вращающего момента на угловую скорость).
Из последней формулы вытекает важное следствие:

(при постоянной мощности вращающий момент обратно пропорционален угловой скорости).
|