Произвольно расположенных сил
Пусть задана система четырех сил  и и 
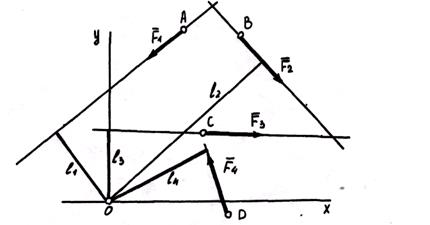
Выберем произвольную точку O – центр приведения – и приведем к нему силу 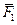 , т.е. перенесем силу , т.е. перенесем силу 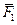 в точку O, присоединим пару сил с моментом в точку O, присоединим пару сил с моментом 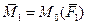 (на рисунке присоединенные моменты изображены круговыми стрелками, направленными в сторону поворота силами (на рисунке присоединенные моменты изображены круговыми стрелками, направленными в сторону поворота силами  и и 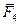 соответствующих плеч соответствующих плеч 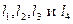 ) )
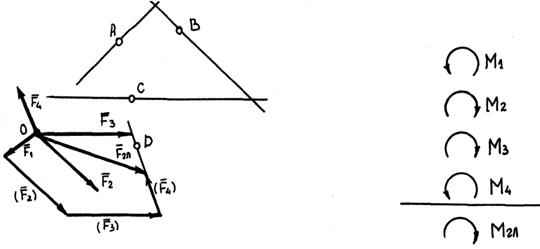
Затем приведем к точке O силу 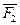 . Перенесем ее в эту точку и присоединим пару с моментом . Перенесем ее в эту точку и присоединим пару с моментом  . Так же поступим с остальными . Так же поступим с остальными
силами 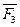 и и 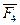 , присоединив пары с моментами , присоединив пары с моментами 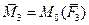 и и  . Как видно из рисунка, в результате последовательного приведения заданных сил к точке образовались система сходящихся сил и система присоединенных пар с моментами, равными моментам заданных сил относительно точки (центра) приведения. . Как видно из рисунка, в результате последовательного приведения заданных сил к точке образовались система сходящихся сил и система присоединенных пар с моментами, равными моментам заданных сил относительно точки (центра) приведения.
С помощью силового многоугольника находим силу 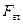 , эквивалентную системе приведенных сил. Сложив алгебраические моменты присоединенных пар, найдем момент одной эквивалентной им пары: , эквивалентную системе приведенных сил. Сложив алгебраические моменты присоединенных пар, найдем момент одной эквивалентной им пары:
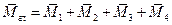
или, так как моменты присоединенных пар равны моментам данных сил относительно центра приведения,
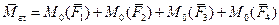
Главный вектор системы: 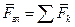
Главный момент системы: 
Произвольная плоская система сил эквивалентна одной силе – главному вектору – и одной паре, момент которой равен главному моменту.
Допустим, что, приведя плоскую систему сил к точке, мы получили главный вектор 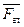 и пару сил с моментом и пару сил с моментом 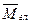 . .
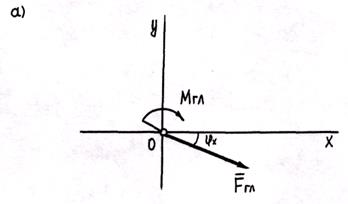
Представим главный момент в виде пары сил (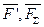 ), численно равных главному вектору ( ), численно равных главному вектору (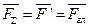 ), и с плечом ), и с плечом 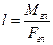 . Расположим эту пару таким образом, чтобы одна из сил оказалась направленной вдоль линии действия главного вектора, но в противоположную сторону. . Расположим эту пару таким образом, чтобы одна из сил оказалась направленной вдоль линии действия главного вектора, но в противоположную сторону.

Тогда силы  и и 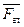 можно исключить как взаимно уравновешенные, а оставшаяся сада можно исключить как взаимно уравновешенные, а оставшаяся сада  и есть искомая равнодействующая рассматриваемой системы сил. и есть искомая равнодействующая рассматриваемой системы сил.
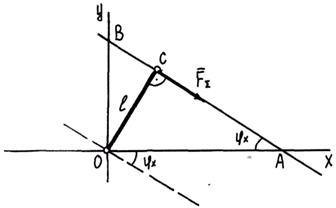
Расстояние от центра приведения до линии действия равнодействующей:

Следовательно, равнодействующая ПСПРС равна главному вектору и расстояние от центра приведения до линии действия равнодействующей равно частному от деления главного момента на модуль главного вектора или равнодействующей.
Теорема Вариньона
Непосредственно из равенства (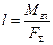 ) вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем предыдущее равенство в таком виде: ) вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем предыдущее равенство в таком виде:
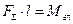
Из последнего рисунка следует, что  – момент равнодействующей относительно любой точки, а по формуле – момент равнодействующей относительно любой точки, а по формуле 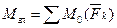 , поэтому последнее равенство можно переписать в виде , поэтому последнее равенство можно переписать в виде
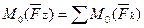 , ,
т.е. момент равнодействующей ПСПРС относительно любой точки равен алгебраической сумме моментов сил системы, взятых относительно той же точки.
|